6.22
假設磁道沿半徑均勻分布,即總磁道數和(1-x)r成正比,設磁道數為(1-x)rk;
由題單個磁道的位數和周長成正比,即和半徑xr成正比,設單個磁道的位數為xrz;
其中r、k、z均為常數。
是以C = (1-x)rk * xrz = (-x^2 + x) * r^2 * kz,即需要-x^2 + x最大,得到x = 0.5。
6.23
seek time : 4 ms
average rotational latency : 0.5 * 60 / 15000 * 1000 = 2 ms
transfer time : 60 / 15000 / 800 * 1000= 0.005 ms
4 + 2 + 0.005 = 6.005 ms
6.24
A.
2MB = 512 bytes * 4096,即需要讀取4096個扇區。
定位時間為:4 + 0.5*60/15000*1000 = 6 ms
最理想的情況下,這4096個扇區都在一個柱面上(一個磁道讀完後繼續讀下一個,磁頭不用移動),也就是4096/1000 = 5個磁道。
即transfer time = 4096 / 1000 * 60 / 15000 * 1000 = 16.384 ms
是以理想時間為:6 + 16.384 = 22.384 ms
B.
在完全随機的情況下,這4096個扇區分布在不同的磁道上,每一個扇區讀完以後磁頭都要再次去定位。
是以總的時間為:6 * 4096 + transfer time = 24592.384 ms (這裡書上有一個類似的題目,但是沒有加上transfer time ,我覺得還是要加上)
6.25
6.26
6.27
0x08A4 0x08A5 0x08A6 0x08A7
0x0704 0x0705 0x0706 0x0707
0x1238 0x1239 0x123A 0x123B
6.28
None
0x18F0 0x18F1 0x18F2 0x18F3
0x00B0 0x00B1 0x00B2 0x00B3
C.
0x0E34 0x0E35 0x0E36 0x0E37
D.
0x1BDC 0x1BDD 0x1BDE 0x1BDF
6.29
CTCTCTCTCTCTCTCT, CICI, COCO
6.30
C = S * E * B = 128 Bytes
CTCTCTCTCTCTCTCT, CICICI, COCO
6.31
00111000, 110, 10
CO 0x2
CI 0x6
CT 0x38
Cache hit? Y
Cache hit? N 2020-6-10
Cache byte returned 0xEB
6.32
10110111, 010, 00
CO 0x0
CI 0x2
CT 0xB7
Cache hit? N
Cache byte returned -
6.33
0x1788 0x1789 0x178A 0x178B
0x16C8 0x16C9 0x16CA 0x16CB
6.34
cache共有兩個block,分别位于兩個set中,設他們為b1和b2。每個block可以放下4個int類型的變量,也就是數組中的一行。在這一題中,源數組和目的數組是相鄰排列的。是以記憶體和cache的映射情況是這樣的:
b1 : src[0][] src[2][] dst[0][] dst[2][]
b2 : src[1][] src[3][] dst[1][] dst[3][]
6.35
cache共有八個block,分别位于八個set中,設他們為b1、b2、b3、b4、b5、b6、b7、b8。每個block可以放下4個int類型的變量,也就是數組中的一行。在這一題中,源數組和目的數組是相鄰排列的。是以記憶體和cache的映射情況是這樣的:(這時不會有沖突)
b1 : src[0][]
b2 : src[1][]
b3 : src[2][]
b4 : src[3][]
b5 : dst[0][]
b6 : dst[1][]
b7 : dst[2][]
b8 : dst[3][]
6.36
cache共有32個block,分别位于32個set中,每個block可以放下4個int類型的變量,是以所有的block可以放下x數組中的一行。由映射關系,x[0][i]和x[1][i]對應的set是一樣的。是以每一次的運算都會發生miss的情況,是以miss rate = 100%。
cache共有64個block,分别位于64個set中,每個block可以放下4個int類型的變量,是以所有的block可以放下x數組中的兩行,即全部放入。每四次讀取中的第一次會發生miss,是以miss rate = 25%。
cache共有32個block,分别位于16個set中,每個block可以放下4個int類型的變量,每個set可以放下8個int類型的變量,所有的block可以放下x數組中的一行。由映射關系,x[0][i]和x[1][i]對應的set是一樣的,x[y][i]和x[y][i+64]對應的set也是一樣的。
對于x[0][0] * x[1][0] ~ x[0][63] * x[1][63] ,每四次運算會有第一次miss。
對于x[0][64] * x[1][64] ~ x[0][127] * x[1][127] ,每四次運算會有第一次miss(擦去前面warm up的cache)。
綜上,miss rate = 25%。
不會,因為此時block大小是限制因素(每四次讀取第一次miss)。
E.
會,更大的block會降低miss rate,因為miss隻發生在第一次讀入block的時候,是以更大的block會使得miss占總讀取的比例降低。
6.37
cache共有256個block,分别位于256個set中,每個block可以放下4個int類型的變量,所有的block可以放下1024個int類型的變量。
當N = 64:
映射關系:a[0][0] ~ a[15][63]、a[16][0] ~ a[31][63]、a[32][0] ~ a[47][63]、a[48][0] ~ a[63][63] 互相重疊。
sumA按照行來讀取,是以每四次讀取第一次都會miss,即miss rate = 25%。
sumB按照列來讀取,是以每一次讀取都會發生miss(讀取後的block又會被覆寫),即miss rate = 100%。
sumC按照列來讀取,但是每次讀取後都會按照行再讀取一次,是以每四次讀取會有兩次miss,即miss rate = 50%。
當N = 60
映射關系:a[0][0] ~ a[17][3]、a[17][4] ~ a[34][7]、a[34][8] ~ a[51][11]、a[51][12] ~ a[59][59]互相重疊,其中最後的a[51][12] ~ a[59][59]沒有到達cache的尾部。
sumB按照列來讀取,這裡的情況有些複雜,我寫了一個程式來分析:
輸出結果為25%。
将上面程式的循環部分更改為:
6.38
這個cache有64個block,每個block可以放4個int類型的變量,也就是一個<code>point_color</code>的結構體,即cache總共可以放置64個結構體。
映射關系為:square[0][0] ~ square[3][15]、square[4][0] ~ square[7][15]、square[8][0] ~ square[11][15]、square[12][0] ~ square[15][15] 互相重疊。
16 * 16 * 4 = 1024
這個程式是按照行來寫的,是以每四次寫入隻有第一次miss,即miss的次數為1024 / 4 = 256
25%
6.39
這個程式是按照列來寫的,每四次寫入隻有第一次miss(每次都完整利用了一個block,沒有讀入block的浪費,此時miss rate隻取決于block的大小),即miss的次數為1024 / 4 = 256
6.40
16 * 16 + 3 * 16 * 16 = 1024
對于第一個循環,每一次寫入都會發生miss的情況,最後cache中儲存的是square[12][0] ~ square[15][15],而第二個循環又從頭開始寫入,是以每三次寫入的第一次都會發生miss。總的miss次數就是16 * 16 * 2 = 512。
50%
6.41
這個cache有16K個block,每個block可以放4個char類型的變量,也就是一個<code>pixel</code>的結構體,即cache總共可以放置16K個結構體。<code>buffer</code>裡面一共有480 * 640 = 300K個結構體,是以映射時會有18個完全重疊的,最後一次重疊3/4.
這個程式按照列來寫,每四次寫入隻有第一次miss(每次都完整利用了一個block,沒有讀入block的浪費,此時miss rate隻取決于block的大小),是以miss rate = 25%。
6.42
這個程式實際上就是按照行來寫的指針版本,每四次寫入隻有第一次miss,miss rate = 25%。
6.43
這個程式實際上還是按照行來寫的指針版本,但是隻寫了buffer數組的1/4。每四次寫入隻有第一次miss,miss rate = 25%。
6.44
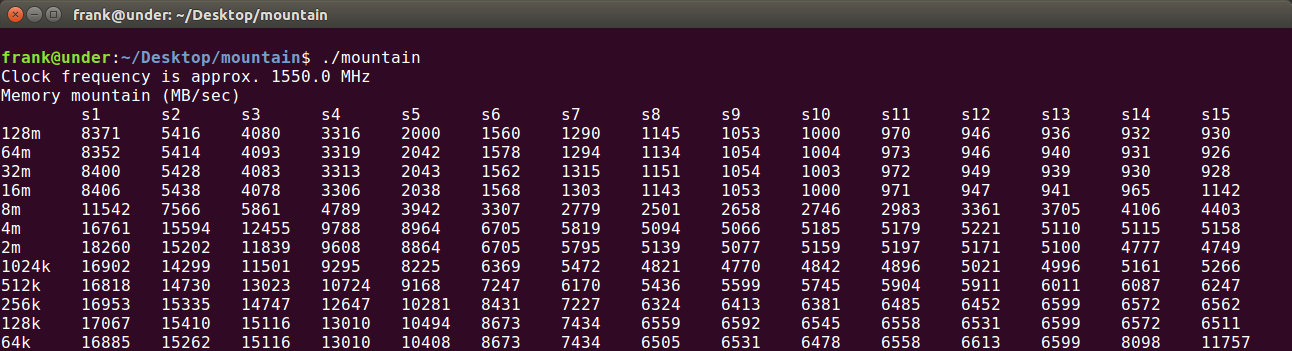
為了辨識緩存的大小,選取中間的列(例如S8)來判斷——避免CPU的prefetching帶來幹擾。可以看出,在32K和512K以及8M的地方有明顯的落差,是以判斷L1:32k、L2:512k、L3:8M。
用<code>lscpu</code>驗證分析正确:
6.45
這個題要求我們利用第5章和第6章中學到的優化知識。對于第5章,就是減少循環的資料依賴,進而利用流水線并行執行;對于第6章,則是從兩個方面(temporary、spatial)利用資料的“本地性”。
以上的關鍵語句中的乘法和加法已經實作了循環之間獨立,src也是按照行讀入的,但是dst卻是按照列讀入的,這樣沒有充分利用每一次讀入的block。于是我們想到可不可以每一次讀入<code>dst[j*dim + i]</code>所在的block之後繼續寫入例如<code>dst[j*dim + i + 1]</code> <code>dst[j*dim + i + 2]</code>這樣的變量,但是這樣有需要src的部分變為<code>src[(i+1)*dim +j]</code>等等,是以我們現在不僅要“橫向”擴充dst,還要“縱向”擴充src,其實這是一種叫做blocking的技術,即每次讀入一塊資料,對此塊資料完全利用後抛棄,然後讀取下一個塊。可以參考csapp網上給的注解:MEM:BLOCKING — Using blocking to increase temporal locality
設我們的資料塊的寬度是B,由于我們要對兩個數組進行讀寫操作,是以2B^2 < C(其中C是cache的容量),在此限制下B盡可能取大。
6.46
這個題僅僅是6.45的一個實踐版。但這個題有一個小技巧,就是<code>G[d] || G[s]</code>這個運算對于G[d]和G[s]都是一樣的,是以隻用計算一次,進而我們隻用計算對角線的上半部分的内容,也就是第二外層循環的j不用從0而是從最外層循環的i開始。