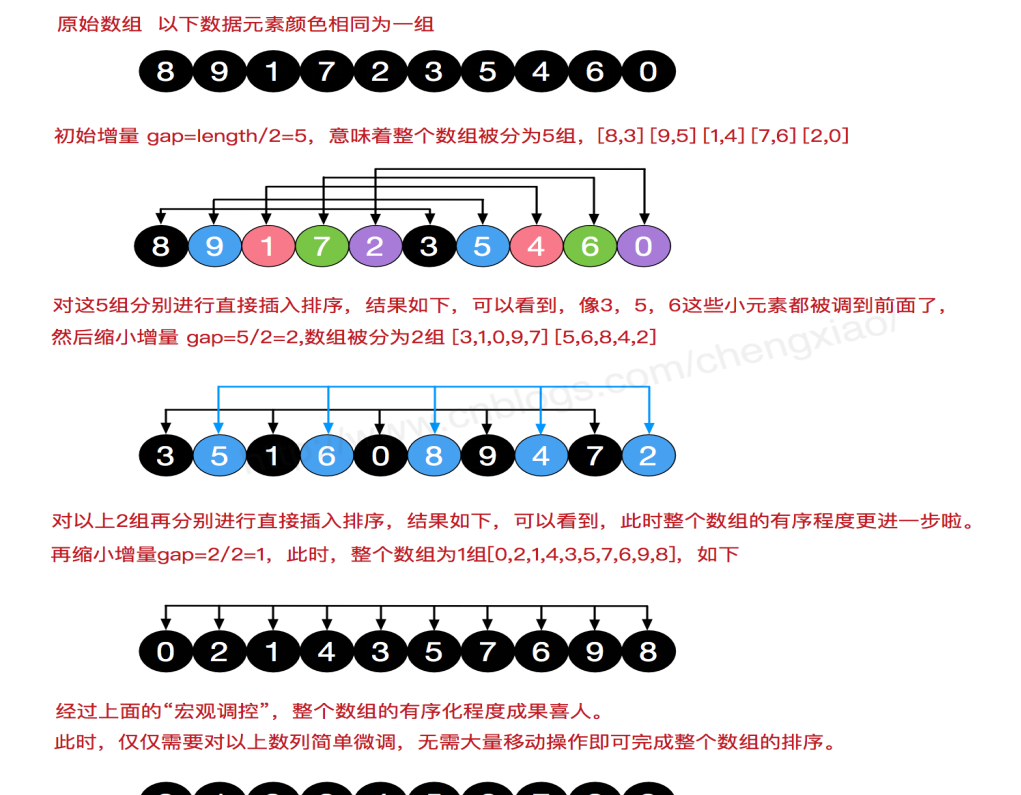
希爾排序相對插入排序來說更加高效,是時間複雜度突破T(n*n)的另一種高效的簡單排序,希爾排序的執行流程可描述為:
一組無序的數列,選擇一個增量,即gap = arr.length/2,以此增量為标的,進行第一趟資料分組與排序,然後縮小增量,繼續以gap = gap/2的方式進行分組和排序,
每趟排序,根據對應的增量ti,将待排序列分割成若幹長度為m 的子序列,分别對各子表進行直接插入排序。僅增量因子為1 時,整個序列作為一個表來處理,表長度即為整個序列的長度。
下面我們用代碼來實作希爾排序,
運作main函數,得到結果,
簡單分析一下希爾排序的性能,可以得出如下結論:
最好的情況下,T(n) = O(nlog2 n)
最壞情況:T(n) = O(nlog2 n)
平均情況:T(n) = O(nlog2 n)