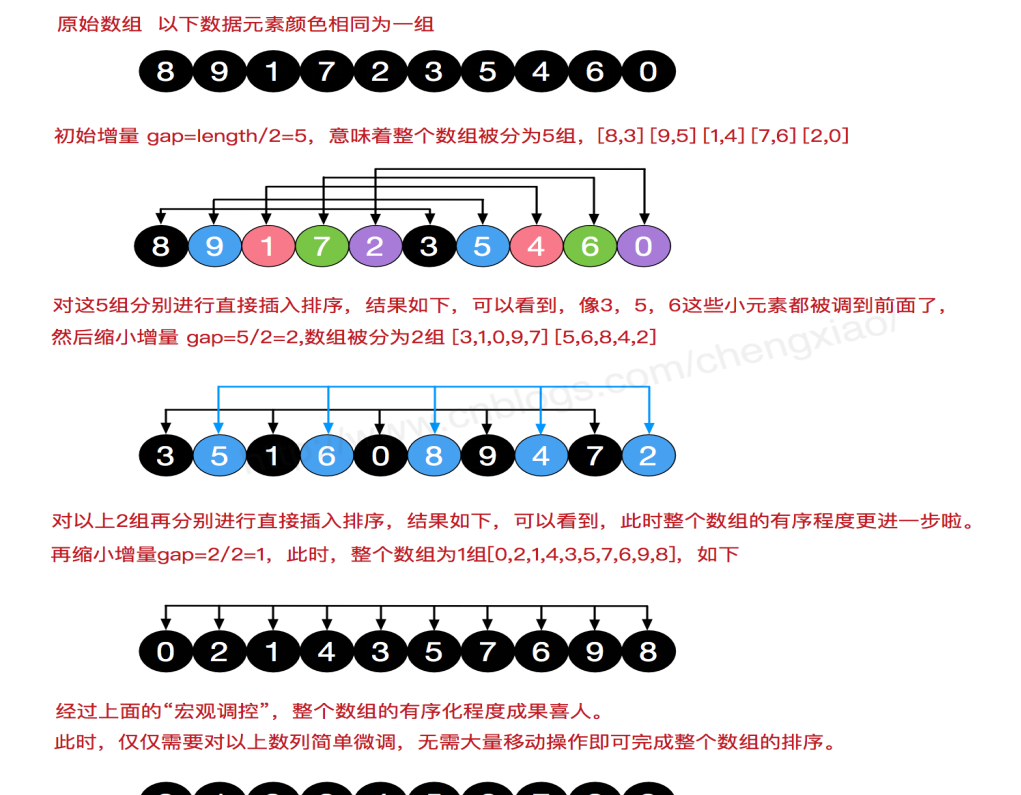
希尔排序相对插入排序来说更加高效,是时间复杂度突破T(n*n)的另一种高效的简单排序,希尔排序的执行流程可描述为:
一组无序的数列,选择一个增量,即gap = arr.length/2,以此增量为标的,进行第一趟数据分组与排序,然后缩小增量,继续以gap = gap/2的方式进行分组和排序,
每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
下面我们用代码来实现希尔排序,
运行main函数,得到结果,
简单分析一下希尔排序的性能,可以得出如下结论:
最好的情况下,T(n) = O(nlog2 n)
最坏情况:T(n) = O(nlog2 n)
平均情况:T(n) = O(nlog2 n)