1 由損失函數引出一堆“風險”
1.1 損失函數
在機器學習中,所有的算法模型其實都依賴于最小化或最大化某一個函數,我們稱之為“目标
最小化的這組函數被稱為“損失函數”。什麼是損失函數呢?
損失函數描述了單個樣本預測值和真實值之間誤差的程度。用來度量模型一次預測的好壞。
損失函數是衡量預測模型預測期望結果表現的名額。損失函數越小,模型的魯棒性越好。
常用損失函數有:
0-1損失函數:用來表述分類問題,當預測分類錯誤時,損失函數值為1,正确為0
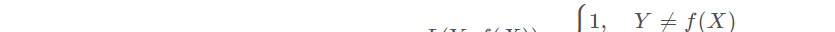
平方損失函數:用來描述回歸問題,用來表示連續性變量,為預測值與真實值內插補點的平方。(誤內插補點越大、懲罰力度越強,也就是對內插補點敏感)
絕對損失函數:用在回歸模型,用距離的絕對值來衡量
對數損失函數:是預測值Y和條件機率之間的衡量。事實上,該損失函數用到了極大似然估計的思想。P(Y|X)通俗的解釋就是:在目前模型的基礎上,對于樣本X,其預測值為Y,也就是預測正确的機率。由于機率之間的同時滿足需要使用乘法,為了将其轉化為加法,我們将其取對數。最後由于是損失函數,是以預測正确的機率越高,其損失值應該是越小,是以再加個負号取個反。
以上損失函數是針對于單個樣本的,但是一個訓練資料集中存在N個樣本,N個樣本給出N個損失,如何進行選擇呢?
這就引出了風險函數。
1.2 期望風險
期望風險是損失函數的期望,用來表達理論上模型f(X)關于聯合分布P(X,Y)的平均意義下的損失。又叫期望損失/風險函數。
1.3 經驗風險
模型f(X)關于訓練資料集的平均損失,稱為經驗風險或經驗損失。
其公式含義為:模型關于訓練集的平均損失(每個樣本的損失加起來,然後平均一下)
經驗風險最小的模型為最優模型。在訓練集上最小經驗風險最小,也就意味着預測值和真實值盡可能接近,模型的效果越好。公式含義為取訓練樣本集中對數損失函數平均值的最小。
1.4 經驗風險最小化和結構風險最小化
期望風險是模型關于聯合分布的期望損失,經驗風險是模型關于訓練樣本資料集的平均損失。根據大數定律,當樣本容量N趨于無窮時,經驗風險趨于期望風險。
是以很自然地想到用經驗風險去估計期望風險。但是由于訓練樣本個數有限,可能會出現過度拟合的問題,即決策函數對于訓練集幾乎全部拟合,但是對于測試集拟合效果過差。是以需要對其進行矯正:
結構風險最小化:當樣本容量不大的時候,經驗風險最小化容易産生“過拟合”的問題,為了“減緩”過拟合問題,提出了結構風險最小理論。結構風險最小化為經驗風險與複雜度同時較小。
1.5 小結
1、損失函數:單個樣本預測值和真實值之間誤差的程度。
2、期望風險:是損失函數的期望,理論上模型f(X)關于聯合分布P(X,Y)的平均意義下的損失。
3、經驗風險:模型關于訓練集的平均損失(每個樣本的損失加起來,然後平均一下)。
4、結構風險:在經驗風險上加上一個正則化項,防止過拟合的政策。
2 最小二乘法
2.1 什麼是最小二乘法
最小二乘法源于法國數學家阿德裡安的猜想:
對于測量值來說,讓總的誤差的平方最小的就是真實值。這是基于,如果誤差是随機的,應該圍繞真值上下波動。
即:
為了求出這個二次函數的最小值,對其進行求導,導數為0的時候取得最小值:
進而:
正好是算數平均數(算數平均數是最小二乘法的特例)。
這就是最小二乘法,所謂“二乘”就是平方的意思。
(高斯證明過:如果誤差的分布是正态分布,那麼最小二乘法得到的就是最有可能的值。)
2.2 線性回歸中的應用
1 matlab版本
2014a
2 參考文獻
[1] 包子陽,餘繼周,楊杉.智能優化算法及其MATLAB執行個體(第2版)[M].電子工業出版社,2016.
[2]張岩,吳水根.MATLAB優化算法源代碼[M].清華大學出版社,2017.
[3]周品.MATLAB 神經網絡設計與應用[M].清華大學出版社,2013.
[4]陳明.MATLAB神經網絡原理與執行個體精解[M].清華大學出版社,2013.
[5]方清城.MATLAB R2016a神經網絡設計與應用28個案例分析[M].清華大學出版社,2018.