數論 + 公式 - HDU 4335 What is N?What is N? Problem's Link: http://acm.hdu.edu.cn/showproblem.php?pid=4335

Mean: 

給你三個數b、P、M，讓你求有多少個n滿足下式。

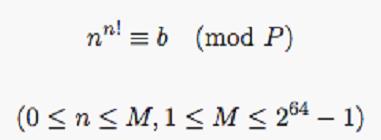
analyse:

看到資料被吓到了，沒半點思路，後來看了解題報告，方法竟然是暴力！

當然暴力是有條件的。

有這樣一個公式：

這個公式的具體證明原來在aekdycoin的百度空間有，但是随着百度空間被轉移(百度作死，流失了好多優質的文章==)，這篇文章的完整版也流失了。

我們就當這個公式是定理吧！

當n!<Phi(C)時，此時我們暴力解決就可。

當n!大于phi（P）的時候，就需要用上面的降幂公式了。

方法還是暴力，n!%phi(p)會出現0，這是必然的，至少n>=phi(p)為0，

那麼(n+1)!%phi(p)也為0，這便出現了重複，轉變為n^(phi(p))%p==b的問題了。

固定了指數，根據鴿巢原理，餘數是循環的，那麼隻要找出p個的結果，之後通過循環節求解便可以了。

Trick:當P為1的時候，b為0，這時候答案是m+1,不過m可能為2^64-1，如果加1的話就會溢出，巨坑。

Time complexity: O(N)

Source code:

/*

* this code is made by crazyacking

* Verdict: Accepted

* Submission Date: 2015-08-25-23.41

* Time: 0MS

* Memory: 137KB

*/

#include <queue>

#include <cstdio>

#include <set>

#include <string>

#include <stack>

#include <cmath>

#include <climits>

#include <map>

#include <cstdlib>

#include <iostream>

#include <vector>

#include <algorithm>

#include <cstring>

using namespace std;

typedef __int64(LL);

typedef unsigned __int64(ULL);

const double eps(1e-8);

LL get_eular(LL m)

{

     LL ret=1;

     for(LL i=2; i*i<=m; i++)

           if(m%i==0)

           {

                 ret*=i-1;

                 m/=i;

                 while(m%i==0)

                 {

                       m/=i;

                       ret*=i;

                 }

           }

     if(m>1) ret*=m-1;

     return ret;

}

long long Quickpow(long long a,long long b,long long m)

     long long ans=1;

     while(b)

     {

           if(b&1) { ans=(ans*a)%m,b--; }

           b/=2,a=a*a%m;

     }

     return ans;

LL b,p,m,ring[100010];

int main()

     int t,Cas=0;

     scanf("%d",&t);

     while(t--)

           scanf("%I64u %I64u %I64u",&b,&p,&m);

           if(p==1)

                 if(m==18446744073709551615ULL)

                       printf("18446744073709551616\n");

                 else

                       printf("%I64u\n",m+1);

                 continue;

           LL i=0,phi=get_eular(p),fac=1,ans=0;

           for(i=0; i<=m&&fac<=phi; i++)

                 if(Quickpow(i,fac,p)==b)

                       ans++;

                 fac*=i+1;

           fac=fac%phi;

           for(; i<=m&&fac; i++)

                 if(Quickpow(i,fac+phi,p)==b)

                 fac=(fac*(i+1))%phi;

           if(i<=m)

                 LL cnt=0;

                 for(int j=0; j<p; j++)

                       ring[j]=Quickpow(i+j,phi,p);

                       if(ring[j]==b)

                             cnt++;

                 LL idx=(m-i+1)/p;

                 ans+=cnt*idx;

                 LL remain=(m-i+1)%p;

                 for(int j=0; j<remain; j++)

                             ans++;

           printf("Case #%d: %I64u\n",++Cas,ans);

     return 0;

}/