反向傳播(Back Propagation)

在利用梯度下降法對神經網絡權重等參數進行訓練時，需要利用反向傳播去計算損失函數對權重參數的偏導數。

下面分析是如何反向傳播的(分析時不考慮偏置項)，

參考上圖，

① 對于一個神經元

       j

      j      

   j，它的輸出被定義為，

          (1.1)

            O

            j

           =

           φ

           (

           n

           e

            t

           )

            ∑

             k

             =

             1

            N

            w

             j

            k

        O_j = \varphi(net_j)=\varphi(\sum_{k=1}^N w_{kj}O_k) \tag{1.1}

    Oj=φ(netj)=φ(k=1∑NwkjOk)(1.1)

其中,

        w

         k

         j

      w_{kj}      

   wkj表示神經元

       k

      k      

   k到

   j之間的權重，

        O

        k

      O_k      

   Ok是上一層神經元的輸出。

       φ

      \varphi      

   φ為激活函數，這裡取為

       l

       o

       g

       i

       s

       t

       c

      logistic      

   logistic函數，

          (1.2)

           z

            1

             +

              e

               −

               z

        \varphi(z)=\frac{1}{1+ e^{-z} } \tag{1.2}

    φ(z)=1+e−z1(1.2)

   logistic函數的求導公式為，

          (1.3)

             d

             φ

              (

              z

              )

             z

            (

            z

            )

            −

            φ

             (

             )

        \dfrac {d\varphi \left( z\right) }{dz}=\varphi\left( z\right) \left( 1-\varphi\left( z\right) \right) \tag{1.3}

    dzdφ(z)=φ(z)(1−φ(z))(1.3)

② 損失函數定義為，

          (1.4)

           E

            2

             t

             −

             y

        E=\dfrac {1}{2}\left( t-y\right) ^{2} \tag{1.4}

    E=21(t−y)2(1.4)

其中，

       y

      y      

   y為輸出層的輸出，

      t      

   t為期望輸出。

考慮

   wkj對于

       E

      E      

   E的影響，是

        j

      O_j      

   Oj間接影響的，是以可得下面的公式(這裡假設

   j前一層神經元為

      i      

   i，即求對

         i

      w_{ij}      

   wij的偏導數)，

          (1.5)

             ∂

             E

              w

               i

               j

              O

              j

             n

             e

              t

        \dfrac {\partial E}{\partial w_{ij}}=\dfrac {\partial E}{\partial O_{j}}\dfrac {\partial O_{j}}{\partial net_{j}}\dfrac {\partial net_{j}}{\partial w_{ij}} \tag{1.5}

    ∂wij∂E=∂Oj∂E∂netj∂Oj∂wij∂netj(1.5)

其中，後兩個偏導數可以直接求出，

         ∂

          O

          j

         n

         e

          t

      \frac{\partial O_{j}}{\partial net_{j}}      

   ∂netj∂Oj參考公式

       1.3

      {1.3}      

   1.3，

          w

           i

           j

       =

        i

      \dfrac {\partial net_{j}}{\partial w_{ij}}=O_i      

   ∂wij∂netj=Oi。但是此時，

         E

      \dfrac{\partial E}{\partial {O_j}}      

   ∂Oj∂E，依然無法求出。不過如果

   j是輸出層，因為

      O_j=y      

   Oj=y，此時可求出

   E對

   Oj的偏導數，

          (1.6)

            ∂

           y

           −

           t

        \dfrac {\partial E}{\partial O_{j}}=\dfrac {\partial E}{\partial y}=\dfrac {\partial }{\partial y}\dfrac {1}{2}\left( t-y\right) ^{2}=y-t \tag{1.6}

    ∂Oj∂E=∂y∂E=∂y∂21(t−y)2=y−t(1.6)

下面就到了最關鍵的一步，此時對于非輸出層，我們無法直接求出

      \frac{\partial E}{\partial {O_j}}      

   ∂Oj∂E，考慮将

   Oj對

   E的作用向

   j的下一層疊代，我們把

   E考慮成一個輸入由

       L

       u

       ,

       v

       …

       w

      L=u,v \dots,w      

   L=u,v…,w這些神經元組成的函數，

   Oj是

      u,v,w      

   u,v,w這些神經元的輸入，

   Oj直接構成了對

       n

       e

        t

        u

        v

      net_u,net_v,net_w      

   netu,netv,netw的影響。

          (1.7)

               O

              n

               t

               u

              ,

               v

              …

               w

        \dfrac {\partial E\left( O_{j}\right) }{\partial O_{j}}=\dfrac {\partial E\left( net_u,net_v,\ldots ,net_{w}\right) }{\partial O_{j}} \tag{1.7}

    ∂Oj∂E(Oj)=∂Oj∂E(netu,netv,…,netw)(1.7)

利用全微分形式，可以擷取到一個遞歸方程，

          (1.8)

             l

             ∈

             L

              ∂

              E

               l

             w

              l

        \dfrac {\partial E}{\partial O_{j}}=\sum _{l\in L}\left( \dfrac {\partial E}{\partial net_{l}}\dfrac {\partial net_{l}}{\partial O_j}\right) =\sum _{l\in L}\left( \dfrac {\partial E}{\partial O_l}\dfrac {\partial O_l}{\partial net_l}w_{jl}\right) \tag{1.8}

    ∂Oj∂E=l∈L∑(∂netl∂E∂Oj∂netl)=l∈L∑(∂Ol∂E∂netl∂Olwjl)(1.8)

通過遞歸方程，我們可以從輸出層開始對需要求的偏導數進行遞歸，是以得名反向傳播。

下面以一個簡單的網絡來對上面的反向傳播結果進行驗證，如下圖所示，

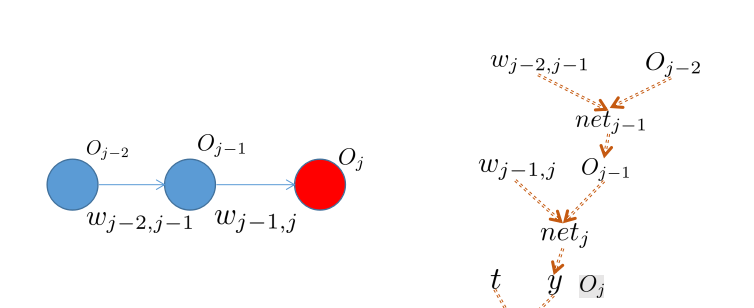
          (1.9)

               1

               ,

        \dfrac {\partial E}{\partial w_{j-1,j}}=\dfrac {\partial E}{\partial O_j}\dfrac {\partial O_j}{\partial net_j}\dfrac {\partial net_j}{\partial w_{j-1,j}} \tag{1.9}

    ∂wj−1,j∂E=∂Oj∂E∂netj∂Oj∂wj−1,j∂netj(1.9)

其中，上式

         y

      \dfrac {\partial E}{\partial O_j}=\dfrac {\partial E}{\partial y}      

   ∂Oj∂E=∂y∂E，三項偏導數都可求出。接着求

           2

           ,

           1

      \dfrac {\partial E}{\partial w_{j-2,j-1}}      

   ∂wj−2,j−1∂E，

          (1.10)

               2

        \dfrac {\partial E}{\partial w_{j-2,j-1}}=\dfrac {\partial E}{\partial O_{j-1}}\dfrac {\partial O_{j-1}}{\partial net_{j-1}}\dfrac {\partial net_{j-1}}{\partial w_{j-2,j-1}}=\dfrac {\partial E}{\partial O_{j}}\dfrac {\partial O_j}{\partial net_j}\dfrac {\partial net_j}{\partial O_{j-1}}\dfrac {\partial O_{j-1}}{\partial net_{j-1}}\dfrac {\partial net_{j-1}}{\partial w_{j-2,j-1}} \tag{1.10}

    ∂wj−2,j−1∂E=∂Oj−1∂E∂netj−1∂Oj−1∂wj−2,j−1∂netj−1=∂Oj∂E∂netj∂Oj∂Oj−1∂netj∂netj−1∂Oj−1∂wj−2,j−1∂netj−1(1.10)

在上式中，

      \dfrac {\partial E}{\partial O_{j-1}}=\dfrac {\partial E}{\partial O_{j}}\dfrac {\partial O_j}{\partial net_j}\dfrac {\partial net_j}{\partial O_{j-1}}      

   ∂Oj−1∂E=∂Oj∂E∂netj∂Oj∂Oj−1∂netj，求

      \dfrac {\partial E}{\partial O_{j-1}}      

   ∂Oj−1∂E時先求出

   E對上一層的

   Oj的偏導數

      \dfrac {\partial E}{\partial O_{j}}      

   ∂Oj∂E，公式(1.10)和(1.8)完全對應，上述過程充分展現了鍊式法則。