PCA(Principal Component Analysis)是一種常用的資料分析方法。PCA通過線性變換将原始資料變換為一組各次元線性無關的表示,可用于提取資料的主要特征分量,常用于高維資料的降維。
一般情況下,在資料挖掘和機器學習中,資料被表示為向量。例如某個淘寶店2012年全年的流量及交易情況可以看成一組記錄的集合,其中每一天的資料是一條記錄,格式如下:
(日期, 浏覽量, 訪客數, 下單數, 成交數, 成交金額)
其中“日期”是一個記錄标志而非路徑成本,而資料挖掘關心的大多是路徑成本,是以如果我們忽略日期這個字段後,我們得到一組記錄,每條記錄可以被表示為一個五維向量,其中一條看起來大約是這個樣子:
(
500
,
240
25
13
2312.15
)
T
(500,240,25,13,2312.15)^T
(500,240,25,13,2312.15)T
我們當然可以對這一組五維向量進行分析和挖掘,不過我們知道,很多機器學習算法的複雜度和資料的維數有着密切關系,甚至與維數呈指數級關聯。當然,這裡區區五維的資料,也許還無所謂,但是實際機器學習中處理成千上萬甚至幾十萬維的情況也并不罕見,在這種情況下,機器學習的資源消耗是不可接受的,是以我們必須對資料進行降維。
降維當然意味着資訊的丢失,不過鑒于實際資料本身常常存在的相關性,我們可以想辦法在降維的同時将資訊的損失盡量降低。
舉個例子,假如某學籍資料有兩列M和F,其中M列的取值是如何此學生為男性取值1,為女性取值0;而F列是學生為女性取值1,男性取值0。此時如果我們統計全部學籍資料,會發現對于任何一條記錄來說,當M為1時F必定為0,反之當M為0時F必定為1。在這種情況下,我們将M或F去掉實際上沒有任何資訊的損失,因為隻要保留一列就可以完全還原另一列。
當然上面是一個極端的情況,在現實中也許不會出現,不過類似的情況還是很常見的。例如上面淘寶店鋪的資料,從經驗我們可以知道,“浏覽量”和“訪客數”往往具有較強的相關關系,而“下單數”和“成交數”也具有較強的相關關系。這裡我們非正式的使用“相關關系”這個詞,可以直覺了解為“當某一天這個店鋪的浏覽量較高(或較低)時,我們應該很大程度上認為這天的訪客數也較高(或較低)”。後面的章節中我們會給出相關性的嚴格數學定義。
這種情況表明,如果我們删除浏覽量或訪客數其中一個名額,我們應該期待并不會丢失太多資訊。是以我們可以删除一個,以降低機器學習算法的複雜度。
上面給出的是降維的樸素思想描述,可以有助于直覺了解降維的動機和可行性,但并不具有操作指導意義。例如,我們到底删除哪一列損失的資訊才最小?亦或根本不是單純删除幾列,而是通過某些變換将原始資料變為更少的列但又使得丢失的資訊最小?到底如何度量丢失資訊的多少?如何根據原始資料決定具體的降維操作步驟?
要準确描述向量,首先要确定一組基,然後給出在基所在的各個直線上的投影值,就可以了。隻不過我們經常省略第一步,而預設以(1,0)和(0,1)為基,也就是自然基。
一個向量在一組機關正交基上的投影,也就是找到向量在對應機關正交基上的坐标。
上述(4)式表明
p
r
o
j
w
y
proj_wy
projwy是
U
U
U的列的線性組合,且對應權值分别為
⋅
u
1
⋯
p
y\cdot u_1 \cdots y\cdot u_p
y⋅u1⋯y⋅up,是個标量,也就是在對應正交基下的坐标值。
舉個例子,自然基下的向量
(
3
,
2
)
T
(3,2)^T
(3,2)T,同時規定了一組新的機關正交基,
(
1
2
−
1
\begin{pmatrix} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{pmatrix}, \begin{pmatrix} \frac{-1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{pmatrix}
(2
12
1),(2
−12
1)
那麼利用上面的投影公式,可以求出在新基下的坐标,用矩陣表示如下,
3
2
=
5
\begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ \frac{-1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 3\\ 2 \end{pmatrix}= \begin{pmatrix} \frac{5}{\sqrt{2}}\\ \frac{-1}{\sqrt{2}} \end{pmatrix}
1)(32)=(2
52
−1)
如果我們有一組N維向量,現在要将其降到K維(K小于N),那麼我們應該如何選擇K個基才能最大程度保留原有的資訊?
假設我們的資料由五條記錄組成,将它們表示成矩陣形式:
1
2
4
3
\begin{pmatrix} 1&1&2&4&2\\ 1&3&3&4&4 \end{pmatrix}
(1113234424)
其中每一列為一條資料記錄,而一行為一個字段。為了後續處理友善,我們首先将每個字段内所有值都減去字段均值,其結果是将每個字段都變為均值為0(這樣做的道理和好處後面會看到)。
我們看上面的資料,第一個字段均值為2,第二個字段均值為3,是以變換後:
−
1
\begin{pmatrix} -1&-1&0&2&0\\ -2&0&0&1&1 \end{pmatrix}
(−1−2−10002101)
我們可以看下五條資料在平面直角坐标系内的樣子:
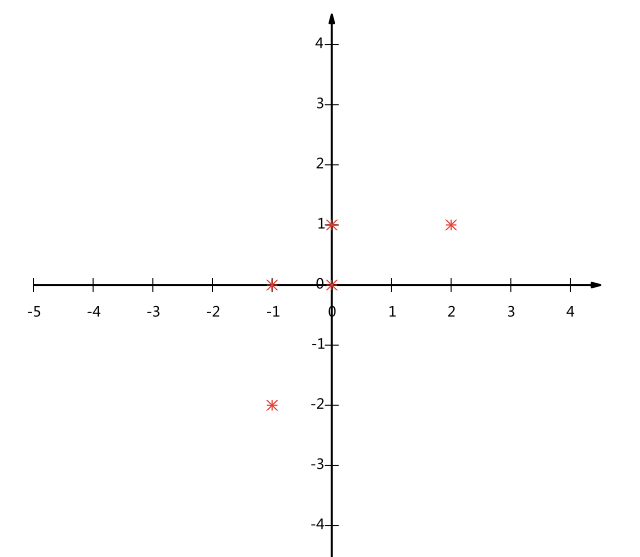
現在問題來了:如果我們必須使用一維來表示這些資料,又希望盡量保留原始的資訊,你要如何選擇?
通過上一節對基變換的讨論我們知道,這個問題實際上是要在二維平面中選擇一個方向,将所有資料都投影到這個方向所在直線上,用投影值表示原始記錄。這是一個實際的二維降到一維的問題。
那麼如何選擇這個方向(或者說基)才能盡量保留最多的原始資訊呢?一種直覺的看法是:希望投影後的投影值盡可能分散。
以上圖為例,可以看出如果向x軸投影,那麼最左邊的兩個點會重疊在一起,中間的兩個點也會重疊在一起,于是本身四個各不相同的二維點投影後隻剩下兩個不同的值了,這是一種嚴重的資訊丢失,同理,如果向y軸投影最上面的兩個點和分布在x軸上的兩個點也會重疊。是以看來x和y軸都不是最好的投影選擇。我們直覺目測,如果向通過第一象限和第三象限的斜線投影,則五個點在投影後還是可以區分的。
下面,我們用數學方法表述這個問題。
上文說到,我們希望投影後投影值盡可能分散,而這種分散程度,可以用數學上的方差來表述。此處,一個字段的方差可以看做是每個元素與字段均值的差的平方和的均值,即:
V
a
m
∑
i
=
1
a
i
−
μ
2
Var(a)=\frac{1}{m}\sum_{i=1}^m(a_i-\mu)^2
Var(a)=m1i=1∑m(ai−μ)2
于上面我們已經将每個字段的均值都化為0了,是以方差可以直接用每個元素的平方和除以元素個數表示:
Var(a)=\frac{1}{m}\sum_{i=1}^m(a_i)^2
Var(a)=m1i=1∑m(ai)2
于是上面的問題被形式化表述為:尋找一個一維基,使得所有資料變換為這個基上的坐标表示後,方內插補點最大。
對于上面二維降成一維的問題來說,找到那個使得方差最大的方向就可以了。不過對于更高維,還有一個問題需要解決。考慮三維降到二維問題。與之前相同,首先我們希望找到一個方向使得投影後方差最大,這樣就完成了第一個方向的選擇,繼而我們選擇第二個投影方向。
如果我們還是單純隻選擇方差最大的方向,很明顯,這個方向與第一個方向應該是“幾乎重合在一起”,顯然這樣的次元是沒有用的,是以,應該有其他限制條件。從直覺上說,讓兩個字段盡可能表示更多的原始資訊,我們是不希望它們之間存在(線性)相關性的,因為相關性意味着兩個字段不是完全獨立,必然存在重複表示的資訊。
數學上可以用兩個字段的協方差表示其相關性,由于已經讓每個字段均值為0,則:
C
v
b
b
Cov(a,b)=\frac{1}{m}\sum_{i=1}^m a_ib_i
Cov(a,b)=m1i=1∑maibi
可以看到,在字段均值為0的情況下,兩個字段的協方差簡潔的表示為其内積除以元素數m。
當協方差為0時,表示兩個字段完全獨立。為了讓協方差為0,我們選擇第二個基時隻能在與第一個基正交的方向上選擇。是以最終選擇的兩個方向一定是正交的。
至此,我們得到了降維問題的優化目标:将一組N維向量降為K維(K大于0,小于N),其目标是選擇K個機關(模為1)正交基,使得原始資料變換到這組基上後,各字段兩兩間協方差為0,而字段的方差則盡可能大(在正交的限制下,取最大的K個方差)。
上面我們導出了優化目标,但是這個目标似乎不能直接作為操作指南(或者說算法),因為它隻說要什麼,但根本沒有說怎麼做。是以我們要繼續在數學上研究計算方案。
我們看到,最終要達到的目的與字段内方差及字段間協方差有密切關系。是以我們希望能将兩者統一表示,仔細觀察發現,兩者均可以表示為内積的形式,而内積又與矩陣相乘密切相關。于是我們來了靈感:
假設我們隻有a和b兩個字段,那麼我們将它們按行組成矩陣
X
X
X:
X
a
2
…
m
b
X= \begin{pmatrix} a_1 & a_2 & \dots & a_m \\ b_1 & b_2 & \dots & b_m \end{pmatrix}
X=(a1b1a2b2……ambm)
然後我們用
X乘以
X的轉置,并乘上系數
1
m
\frac{1}{m}
m1:
X
m
∑
i
=
1
a
i
b
\frac{1}{m}XX^T= \begin{pmatrix} \frac{1}{m}\sum_{i=1}^m a_i^2 & \frac{1}{m}\sum_{i=1}^m a_ib_i \\ \frac{1}{m}\sum_{i=1}^m a_ib_i & \frac{1}{m}\sum_{i=1}^m b_i^2 \end{pmatrix}
m1XXT=(m1∑i=1mai2m1∑i=1maibim1∑i=1maibim1∑i=1mbi2)
奇迹出現了!這個矩陣對角線上的兩個元素分别是兩個字段的方差,而其它元素是a和b的協方差。兩者被統一到了一個矩陣的。
根據矩陣相乘的運算法則,這個結論很容易被推廣到一般情況:
設我們有m個n維資料記錄,将其按列排成n乘m的矩陣X,設
C=\frac{1}{m}XX^T
C=m1XXT,則C是一個對稱矩陣,其對角線分别個各個字段的方差,而第i行j列和j行i列元素相同,表示i和j兩個字段的協方差。
根據上述推導,我們發現要達到優化目的,等價于将協方差矩陣對角化:即除對角線外的其它元素化為0,并且在對角線上将元素按大小從上到下排列,這樣我們就達到了優化目的。這樣說可能還不是很明晰,我們進一步看下原矩陣與基變換後矩陣協方差矩陣的關系:
設原始資料矩陣X對應的協方差矩陣為C,而P是一組基按行組成的矩陣,
Y
=
P
Y=PX
Y=PX,則
Y
Y為
X對
P
P做基變換後的資料。設
Y的協方差矩陣為
D
D
D,我們推導一下
D與
C
C
C的關系:
D
=
m
Y
Y
T
(
P
X
)
)
X
P
C
\begin{aligned} D &= \frac{1}{m}YY^T \\ &= \frac{1}{m}(PX)(PX)^T\\ &= P(\frac{1}{m}XX^T)P^T\\ &= PCP^T \end{aligned}
D=m1YYT=m1(PX)(PX)T=P(m1XXT)PT=PCPT
現在事情很明白了!我們要找的
P不是别的,而是能讓原始協方差矩陣對角化的
P。換句話說,優化目标變成了尋找一個矩陣
P,滿足
P
PCP^T
PCPT是一個對角矩陣,并且對角元素按從大到小依次排列,那麼
P的前
K
K
K行就是要尋找的基,用
K行組成的矩陣乘以
X就使得
X從
N
N
N維降到了
K維并滿足上述優化條件。
總結一下PCA的算法步驟:
設有m條n維資料。
将原始資料按列組成n行m列矩陣X
将X的每一行(代表一個屬性字段)進行零均值化,即減去這一行的均值
求出協方差矩陣
C=m1XXT
求出協方差矩陣的特征值及對應的特征向量
将特征向量按對應特征值大小從上到下按行排列成矩陣,取前k行組成矩陣P
Y
Y=PX
Y=PX即為降維到k維後的資料
這裡以上文提到的
\begin{pmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 &1 &1 \end{pmatrix}
為例,我們用PCA方法将這組二維資料其降到一維。
因為這個矩陣的每行已經是零均值,這裡我們直接求協方差矩陣
5
−
6
4
C=\frac{1}{5} \begin{pmatrix} -1 & -1 & 0 & 2 & 0\\ -2 & 0 & 0 & 1 & 1\\ \end{pmatrix} \begin{pmatrix} -1 & -2\\ -1 & 0 \\ 0 & 0\\ 2 & 1\\ 0 & 1 \end{pmatrix} =\begin{pmatrix} \frac{6}{5} & \frac{4}{5} \\ \frac{4}{5} & \frac{6}{5} \end{pmatrix}
C=51(−1−2−10002101)⎝⎜⎜⎜⎜⎛−1−1020−20011⎠⎟⎟⎟⎟⎞=(56545456)
然後求其特征值和特征向量,求解後特征值為:
λ
2
/
5
\lambda_1=2 , \lambda_2=2/5
λ1=2,λ2=2/5
其對應的特征向量分别是:
c
c1 \begin{pmatrix} 1\\ 1 \end{pmatrix}, c2 \begin{pmatrix} -1\\ 1 \end{pmatrix}
c1(11),c2(−11)
其中對應的特征向量分别是一個通解,
c
1
c1
c1和
c2
c2可取任意實數。那麼标準化後的特征向量為:
\begin{pmatrix} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\\ \end{pmatrix}, \begin{pmatrix} \frac{-1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{pmatrix}
是以我們的矩陣P是:
P= \begin{pmatrix} \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{-1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}
P=(2
可以驗證協方差矩陣
C的對角化:
P
PCP^T= \begin{pmatrix} \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{-1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} \frac{6}{5} & \frac{4}{5} \\ \frac{4}{5} & \frac{6}{5} \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}}& \frac{-1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} =\begin{pmatrix} 2 & 0\\ 0 & \frac{2}{5} \end{pmatrix}
PCPT=(2
1)(56545456)(2
1)=(20052)
最後我們用P的第一行乘以資料矩陣,就得到了降維後的表示:
3
3
Y= \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} -1 & -1 & 0 & 2 & 0\\ -2 & 0 & 0 & 1 & 1\\ \end{pmatrix} =\begin{pmatrix} \frac{-3}{\sqrt{2}} & \frac{-1}{\sqrt{2}} & 0 & \frac{3}{\sqrt{2}} & \frac{-1}{\sqrt{2}} \end{pmatrix}
Y=(2
1)(−1−2−10002101)=(2
−32
−102
32
降維投影結果如下圖: