坐标旋轉是個啥概念呢?
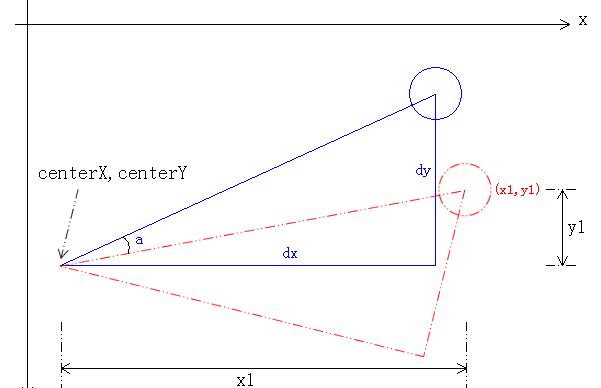
如上圖,(藍色)小球 繞某一中心點旋轉a角度後,到達(紅色)小球的位置,則紅色小球相對中心點的坐标為:
x1 = dx * cos(a) - dy * sin(a)
y1 = dy * cos(a) + dx * sin(a)
這個就是坐标旋轉公式,如果要反向旋轉,則公式要修正一下,有二種方法:
1.将a變成-a,即:
x1 = dx * cos(-a) - dy * sin(-a)
y1 = dy * cos(-a) + dx * sin(-a)
2.将正向旋轉公式中的相減号交換
x1 = dx * cos(a) + dy * sin(a);
y1 = dy * cos(a) - dx * sin(a);
先來回顧一個經典的小球圓周運動:
這個沒啥特别的,接下來我們用坐标旋轉公式換一種做法驗證一下是否有效:
效果完全相同,說明坐标旋轉公式完全是有效的,問題來了:原本一個簡單的問題,經過這樣複雜的處理後,效果并沒有變化,為何要化簡為繁呢?
好處1:提高運作效率
下面示範的多個物體旋轉的傳統做法:
坐标旋轉的新做法:
對比代碼可以發現,同樣的效果用坐标旋轉處理後,Math的調用全部提升到循環外部了,對于30個小球來講,每一幀至少減少了30 * 4 = 120次的三角函數運算
好處2:可以友善的處理斜面反彈
先來看下正向/反向旋轉的測試
對于水準或垂直的反彈運動,實作起來并不複雜,但對于斜面而言,情況就複雜多了,首先:物體反彈并不是光學中的反射,是以用“入射角=反射角”來模拟并不準确,其次我們還要考慮到重力因素/摩擦力因素,這些都會影響到速度的大小和方向。
如果用坐标旋轉的思維方式去考慮這一複雜的問題,解決辦法就變得非常簡單。
所有向量(實體學中也常稱矢量,雖然這二者在嚴格意義上講并不相同)都可應用坐标旋轉,我們可以把整個系統(包括斜面以及相對斜面運作物體的速度向量)都通過坐标旋轉變成水準面或垂直面,這樣就把問題簡單化了,等一切按水準或垂直的簡單方式處理完成以後,再把系統旋轉回最初的樣子。
多角度斜面反彈: