女士們,先生們,老少爺們兒們!在下張大少。
1 引言
伊斯蘭星形圖案代表了世界上偉大的裝飾設計傳統之一[2, 6, 7]。星形圖案是數學、藝術和精神的和諧融合,是對稱性、平衡性和獨創性的表現。
星形圖案還展現了一個持久的數學之謎。大部分的原始設計技術已經湮沒在曆史中,我們不得不通過古代工匠和數學家留下的圖案來探究他們的思想。許多學者和業餘愛好者已經發現或重新發現了生成伊斯蘭圖案的技術[1, 9, 11, 20]。
本文提出了一種基于漢金的"多邊形接觸法"[12]的簡單技術。漢金的方法在給定平面密鋪的基礎上生成伊斯蘭星形圖案(第3節)。通過略微修改結構,我們能夠按照Huff的拼花變形風格建構設計[16,第10章](第3.1節)。最後,我們展示了一個被稱為"玫瑰花變換"的密鋪操作如何使用漢金方法(第4節)擴充可用圖案的範圍。花環變換展示了漢金方法的強大功能,并形式化了某些星形圖案類别之間以前無法解釋的關系。
2先前的工作
我們的方法直接借鑒了Kaplan和Salesin[18]的最新研究成果。他們通過用星形圖案的碎片填充拼塊來建構設計。對于規則多邊形的拼塊,他們給出了一個參數化的"設計元素"空間,這些元素來自曆史上的例子。然後他們通過使用"推理算法"填充不規則多邊形來完成圖案。由于他們的構造獨立于歐幾裡得的平行公理,他們可以在歐幾裡得和非歐幾裡得的幾何中無縫地繪制星形圖案。我們通過消除設計元素和對所有拼塊統一應用推理算法來簡化他們的方法。我們仍然可以通過将更多的資訊轉移到底層拼塊中來産生複雜的元素,如玫瑰花。這兩個系統産生的設計有很大的重疊性——給定合适的拼塊,Najm系統可以重制這裡介紹的所有星形圖案。但本文提供了對支撐星形圖案的拼塊的見解,并提供了一種更簡單和更容易控制的技術。
Jay Bonner是一位廣泛研究伊斯蘭星形圖案的建築師。在一份未發表的手稿[3]中,邦納給出了一個系統的星形圖的展示,這些星形圖是在巨大的密鋪空間(他稱之為"多邊形子網格")上形成的。書中的一些技術也出現在最近的論文[4]中。Bonner的工作是作為設計師的資源,而不是軟體編寫人員的規範。他使用CAD工具手工繪制圖案。本文在一定程度上試圖将他的技術基礎上的算法形式化,并将這些算法用軟體表達給建築師、設計師和藝術家。
3接觸多邊形方法
基于拼塊的伊斯蘭星形圖案的方法似乎是由E.H.Hankin在20世紀初在西方提出的。在一系列的論文中[12, 13, 14, 15],他解釋了他的發現并給出了許多關于如何使用該技術的例子。漢金對其技術的描述為算法方法提供了一個很好的起點(并有助于推動如今Bonner的工作)。
在制作這樣的圖案時,首先需要用由接觸多邊形組成的網絡覆寫要裝飾的表面。然後,通過每個多邊形的每條邊的中心繪制兩條線。這些線互相交叉,就像字母X一樣,并一直延續到它們與其他來源相似的線相遇。這樣就完成了圖案[12,第4頁]。
從那時起,Lee[19]和Critchlow[8]等學者都提到了漢金的"多邊形接觸"技術。這種方法立即提出了一種将密鋪圖變成伊斯蘭星形圖案的算法。給定一個由多邊形組成的平面圖(漢金的 "網絡"),我們把平面圖邊緣的中點确定為"接觸點",設計将在這裡誕生。我們在每個接觸點放置一個小的X,然後 "生長"X的手臂,直到它們遇到從其他接觸點增長的線條。在這個過程中,有一個明顯的自由度:X的臂與它們所發出的邊所形成的角度。我們稱這個角度為圖案的接觸角。圖1(a)中給出了一個說明。
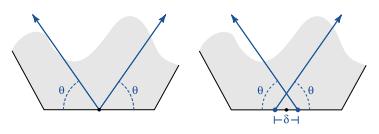
圖1
圖1:在漢金方法的第一步中,每個貼圖上的每個接觸位置都對應着一對射線。在(a)中,單個接觸位置得到兩條射線,每一條射線與邊緣形成接觸角θ。在(b)中,我們用距離δ來分離射線源。
我們可以把這個過程看作是在一個拼塊中為每個獨特的拼塊形狀生長一個小的線條排列。我們從拼塊邊緣的中點向内形成一對射線,形成半個X。我們把與一塊拼塊相關的線條的排列稱為它的主題。這種構造技術的實作應該接受一個密鋪和一個接觸角作為輸入,為每個密鋪形狀建構一個圖案,然後将這些圖案組裝成一個可以裝飾的圖案。
給定一個正n邊形拼塊和一個接觸角,我們必須從通過其邊緣中點進入該拼塊的2n條射線中開發一個圖案。一個成功的圖案将把射線分成幾對,其中每一對比對的射線代表了一條通過拼塊的獨特路徑。最好的圖案将是能優化所選美學目标的光線配對。我們選擇了一個簡單的目标:最小化圖案中所有線段的長度之和。這個目标反映了伊斯蘭設計中的經濟性和必然性,并通過許多曆史上的例子得到了證明。
那麼,在理想情況下,我們将周遊所有可能的射線配對,并找到總長度最小的那個。不幸的是,這種算法并不實用——有n!(n/2)!2n種方法可以将2n條射線分割成一對,或者對于一個有10條邊的區域來說,有超過5億種可能性。
相反,我們使用一種貪婪的方法,基于Kaplan和Salesin的推理算法的簡化版本[18]。我們考慮所有可能的射線對。如果兩條射線→AB和→CD相交于點P,我們将這對射線存儲在一個集合中,其成本等于AP和PD的長度之和。如果這兩條射線是相鄰的,并且互相指向對方,我們就把這一對射線和長度AD放在一起。然後我們可以按成本對集合進行排序,并按順序走過它。對于每一對射線,隻要這對射線還沒有被使用過,我們就把這對射線的路徑納入圖案中。
在實踐中,這種算法在各種各樣的多邊形上表現良好。當然,它在規則多邊形上的表現是完美的,它在那裡建構了星形圖案。它有時會産生具有不比對射線的圖案,有時會産生離底層拼塊太遠的路徑。在它失敗的情況下,通常不是因為它貪婪,而是因為配對技術不适合有關的拼塊形狀。在某些情況下,可以通過将接觸點從邊緣中點移開來改善推斷的圖案。第4節将更詳細地讨論這種調整。
圖2說明了從接觸位置生長射線的過程。圖3顯示了一些典型的設計,這些設計可以通過使用我們對漢金方法的實施而産生。
圖2
圖2:漢金方法的示範。在左邊,接觸點生長出x形的射線排列,直到它們遇到其他射線。當原始的密鋪被移除時,結果就是右邊的圖案。
圖3
圖3:使用漢金方法建構的星圖示例。每一行都顯示了一種密鋪和三種設計,這些設計可以使用三種不同的接觸角從密鋪中派生出來。最下面一行的特色是由近乎規則的多邊形進行的有趣的密鋪。它轉載自Grunbaum and Shephard[10,第64頁],提醒人們過度依賴數字的危險。一個相關的設計也出現在Bourgoin[6,版圖163]中。
在有些情況下,對基本推理算法的簡單修改可以改善生成的圖案。例如,考慮圖4(a)中給出的星形圖案。這個圖案包含大面積的區域,來自于正十二邊形,沒有被填滿。一個更有吸引力的圖案可以通過推理算法的第二遍來建構,從第一遍推理的射線相遇的點向内建構。由此産生的設計,如圖4(b)所示,與傳統更加一緻。在推理算法中,很容易識别出所提供的拼塊形狀是一個規則的多邊形,并在藝術家指定的時候運作第二輪推理。Kaplan和Salesin[18]通過對可用于填充規則多邊形的圖案範圍提供更明确的參數化來解決這個問題。
圖4
圖4:對推理算法的擴充可以産生一個稍微有吸引力的圖案的兩種情況的示範。在(a)中,一個星形圖案顯示了大面積的未填充區域,這些區域是原始拼塊中的規則十邊形的中心。在圖案的内部添加一層推斷的幾何圖形,産生了(b)中的改進設計。這個過程在(c)和(d)中用不同的拼塊重複。
一個進一步的改進是允許接觸位置一分為二,如圖1(b)所示。分割可以通過為推理算法提供第二個實值參數δ來完成,該參數指定了射線的新起點之間的距離。參數δ可以從零(給出原始結構)到拼塊中最短的拼塊邊緣的長度變化。這種修改可以得到Bonner所說的 "兩點圖案",這是一組在伊斯蘭藝術中具有重要曆史意義的圖案[3]。使用δ參數建構的兩點圖案的例子顯示在圖5中。與兩點圖案相對應的設計往往是由非常短的封閉線組成的,每條封閉線都圍繞着原始拼塊的一個頂點形成一個環形。接觸角通常選擇45◦,在拼塊邊緣的中點周圍形成正方形。
圖5
圖5:用漢金的方法構造的兩點星形圖案的例子。每一行顯示了一個模闆拼塊,一個δ=0的星形圖案,以及一個δ非零的相關兩點圖案。
伊斯蘭拼花變形
拼花變形是一種裝飾設計風格,由威廉-赫夫創造,後來由侯世達[16,第10章]推廣。它們是一種"空間動畫",一種在空間而不是時間上進行平滑過渡的幾何圖形。拼花變形與M.C.埃舍爾的變形版畫[5,第280頁]密切相關,盡管與埃舍爾的作品不同,它們是純粹的抽象幾何構成。
利用漢金的方法,我們可以引入一種新的伊斯蘭設計風格,我們稱之為"伊斯蘭鑲木地闆變形"。我們簡單地修改推理算法,使接觸角沿着一條線變化。一條射線的接觸角是根據該射線的起始位置的水準位置的函數來選擇的。這樣一來,離開一個給定的接觸位置的四條射線仍然形成一個X,即使接觸角在一個單一的拼塊内可能有所不同。
接觸角的平滑變化導緻了輕微變化的幾何設計,仍然可以辨認出伊斯蘭風格(參見圖6)。我們認為,這些鑲木地闆變形在伊斯蘭幾何藝術世界中占據了一個有趣的位置。這種結構在伊斯蘭傳統中是顯而易見的,但它們不會在曆史上産生,因為幾乎沒有重複。手工繪制出不斷變化的形狀,然後執行它們的工作,會考驗昔日工匠的耐心。
圖6
圖6:基于漢金方法的伊斯蘭拼花變形。上圖顯示了根據射線起點的水準位置不斷改變射線的接觸角的效果。當這個過程被帶到所有其他的拼塊上時,中間的設計就出現了。在這個設計中,接觸角從側面的最小22.5◦到中間的67.5◦不等。在底部的設計中,接觸角從兩側的36◦到中間的72◦不等。
4 .玫瑰花變換
漢金接觸多邊形法的一個奇特特性是,在适當的接觸角選擇下,不同的密鋪可能産生相同的星形圖案。圖7中最上面一行的圖案就是一個例子。它可以産生的拼塊在左邊使用54°的接觸角,在右邊使用36◦的接觸角。是以,我們可能會懷疑這兩個拼塊之間的關系。
圖7
圖7:不同的拼塊可以産生相同的伊斯蘭設計的例子。在兩種情況下,左邊的密鋪都是使用設計元素和推理的組合來填充的,而右邊的密鋪則單獨使用推理。他們在中心的共享設計中相遇。
這種關系的進一步證據可以在Kaplan和Salesin[18]的Najm系統産生的星形圖案中找到。圖7的底排顯示了左邊的拼塊,其"玫瑰花"圖案放置在規則的十邊形中。Kaplan和salesin提供了這些玫瑰花的明确參數化。但是圖的右邊展示了同樣的圖案可以通過推理單獨從表面上相關的拼塊中産生。
我們對漢金方法的經驗表明,有許多對拼塊以這種方式相關。參照圖7,我們将左邊的密鋪稱為"Najm密鋪",将右邊的密鋪稱為"漢金密鋪"。這兩個有相似的結構,除了在漢金拼塊大的正多邊形是由潛在的不規則多邊形,通常是五邊形的環分開。
在他的手稿[3]中,邦納使用了這兩種拼貼來創造星形圖案,他也觀察到一個單一的設計可能源于多個拼貼。在本節中,我們将介紹一種稱為"玫瑰變換"的密鋪變換,它解釋了Najm密鋪和漢金密鋪之間的聯系。我們還将我們的方法與Najm的方法進行了比較,即每種方法都能産生的圖案。
玫瑰變換的算法讓人聯想到第3節中使用的推理算法。給定一個拼塊,它為每個不同的拼塊形狀構造一個平面圖。然後,這些平面圖被組裝起來,這次是組裝成一個新的拼塊,而不是一個最終設計。這也是一種二進制化:最常見的操作是将垂直平分線豎立到原始拼塊的邊上。每個拼塊形狀的圖紙是以兩種方式之一建構的。
正多邊形。如果拼塊是半徑為r的正n邊形P,且具有五條或更多邊,則貼圖的構造如圖8所示。我們建構一個半徑為R0<r的新正則n-多邊形P0,并将其放置在與原始多邊形同心但相對于其旋轉π/n的位置。然後,我們添加連接配接P0的頂點和P的邊中點的線段。選擇内半徑R0是為了使這些新線段中的每一條的長度正好是P0邊長的一半。一些三角學表明,給定n和r,r0的正确值由下式給出
傳回的圖紙是P0以及連接配接它到P的邊緣中點的線段。
圖8
圖8:應用于正多邊形的玫瑰花形變換。這裡,半徑為r的正10邊形填充了半徑為r0的較小的正10邊形,以及将内多邊形的頂點連接配接到外多邊形的邊中點的線段。選擇内徑是為了使标記的邊具有相同的長度。
不規則多邊形。如果拼塊是一個不滿足上述條件的多邊形P,我們将P的邊的垂直平分線向其内部延伸,如圖9所示。在它們相交的地方截斷分界線。其結果成為這塊拼塊的圖紙。
圖9
圖9:應用于不規則多邊形的玫瑰花環變換。在左側,将為每條拼塊邊緣繪制一條垂直平分線,作為指向拼塊内部的射線。與推理算法一樣,射線在彼此相遇時會被截斷。
這一步在實質上類似于90◦接觸角的推理算法。我們不期望它對每一個可能的多邊形都傳回一個有意義的答案,但是在Najm拼塊中出現的多邊形的情況下,它發現的圖紙通常是合适的。
一些啟發式算法在這裡也起作用,但在推理算法中并不适用。一個适度成功的啟發式方法是考慮所有成對射線的交點,并對位于拼塊内的那些點進行聚類。然後,每個聚類可以被平均到一個點上,所有對該聚類有貢獻的射線都可以将其作為端點。這種調整可能會使一些射線偏離垂直方向,進而在轉換後的拼塊邊緣的中間位置引入"扭結"。我們可以在以後通過檢測結點并将其替換為直線段來糾正這個問題。
當此算法在Najm密鋪上運作時,它傾向于生成漢金密鋪。例如,圖8和圖9中的兩個密鋪對應于圖7左側的Najm密鋪。玫瑰變換在圖的右側生成漢金密鋪。圖10給出了另外兩個密鋪及其玫瑰花形轉換的示例。
圖10
圖10:玫瑰花結轉換的兩個示範。轉換後的密鋪顯示為粗體疊加在原始密鋪上。
玫瑰花變換将卡普蘭和Salesin的"設計元素"中的智慧提取出來,并将其嵌入到拼塊中。假設在給定的密鋪中,Najm用于用玫瑰花環填充正多邊形P。在該密鋪的玫瑰花環變換中,P的縮小副本P0将被不規則五邊形的環包圍。用我們的方法,這些五角形将合力形成圍繞在P0内的一顆中心恒星周圍的六角形花環。玫瑰花環變換的動機(并以此命名)的目标是使五邊形盡可能地接近規則,産生的玫瑰花環在Lee[19]給出的意義上幾乎是理想的。
在某些情況下,漢金的方法在應用于玫瑰花環變換的拼塊時會産生不令人滿意的圖案。圖11顯示了一個示例,其中漢金的方法發現了正确圖案的拓撲,但生成了不均勻的玫瑰花環。邦納讨論了如何在必要時通過調整五邊形上遠離中心的接觸位置來糾正這種情況。然而,他沒有給出何時或如何進行這一調整的迹象。
圖11
圖11:漢金的方法生成不完美的玫瑰花環的一個例子。在(A)中,Najm被用來在正八角形内放置完美的玫瑰花環。當漢金的方法用于(B)中的玫瑰花環變換時,玫瑰花環六邊形(以陰影顯示)有兩種不同的大小。
我們可以求助于拼塊和它們的花環變換之間的關系來解開這個謎團。圖11(A)的設計是使用Najm方法建構的。我們選擇玫瑰花來填充正常的八邊形拼塊。根據設計,玫瑰花環的六邊形手臂(其中兩個在圖中顯示為陰影)與其周圍八邊形的邊緣接觸。
在圖11(B)中,玫瑰花臂是由在玫瑰花環變換中引入的五邊形環形成的。其中一個五邊形的結構如圖12所示。問題是AE和BE的長度不同。如果我們簡單地将接觸位置放置在邊緣中點,則沿邊AB和CD的接觸位置與其相鄰八角形的中心的距離不相等,進而産生不均勻的玫瑰花臂排列。盡管着色的五邊形在拓撲上與其包含的頂點是對偶的,但它不是對偶的(其邊不會被原始密鋪一分為二)。我們通過記錄玫瑰花變換與原始拼貼的交點,并将它們作為接觸位置來糾正這種差異。
圖12
圖12:漢金方法中恢複完美花環的接觸位置調整的圖解。水準線表示玫瑰花變換中着色拼塊邊緣的中點。但是接觸點的正确位置是該邊與原始密鋪的邊的交點。
是以,這兩種密鋪之間存在着深刻的聯系,這可能會暴露出看似武斷但必要的調整背後的邏輯。此外,在計算玫瑰花環變換時,這些修正的接觸位置可以很容易地計算出來。
5 實施
我們已經将本文描述的方法作為一個獨立的Java應用程式來實作。該應用程式的界面顯示了一個疊加了相應伊斯蘭星形圖案的拼塊。使用者能夠選擇要使用的拼塊,并修改用于産生兩點圖案的接觸角θ和距離δ。他們還可以選擇是否在大型規則多邊形中加入推理算法的第二遍,以及是否如第4節末尾所述調整遠離邊緣中點的接觸位置。所有這些變化都以互動方式反映在設計中,使得浏覽各種星形圖案變得容易和愉快。當使用者決定了一個設計後,他們可以使用首先為Taprats[17]開發的裝飾風格來渲染它。圖13中顯示了一個裝飾的圖案。
圖13
圖13:使用接觸多邊形方法制作的裝飾星形圖案
我們目前的軟體隻處理周期性的密鋪(盡管在基礎技術中沒有這種限制)。一個密鋪是由兩個平移向量和一個未變換的多邊形集合表示的。每個多邊形都有一個變換清單,将其地圖到單一平移單元中的出現。這些資訊足以用密鋪的一個子集來覆寫平面的任何區域。在互動式設計器中,代表圖案的平面圖與拼塊形狀相關,并與它們一起繪制。一個獨立的Java應用程式可以用來手工建構周期性的拼塊。使用者可以建立規則的多邊形拼塊并将它們扣在一起,用新的拼塊填充不規則的孔,并指定平移矢量。另一個程式接受周期性密鋪作為輸入,并計算其玫瑰花形變換。
伊斯蘭拼花地闆變形的建構需要多次單獨調用推理算法,目前速度太慢,無法互動運作。它是作為指令行應用程式實作的,該應用程式根據指定邊界框和接觸角度範圍的參數建構設計。
6未來工作
盡管漢金的方法結合了玫瑰花環變換的力量,但一些重要的曆史模式仍然遙不可及。圖14中給出了一個例子。使用Kaplan和Salesin的Najm可以很容易地從十二邊形和三角形的密鋪中建構該圖案。他們的技術為十二角形中的圖案提供了一種明确的參數化,他們稱之為"擴充花環"。人們很容易認為,我們可以通過在此密鋪上進行兩次玫瑰花環變換疊代來獲得相同的模式。仔細觀察發現,在直線相交的地方,它們形成30◦和60◦的角。此圖案的任何基于推理的表示都需要允許多個不同的接觸角,或者在推理算法中進行非貪婪選擇。無論哪種方式,都需要更多的工作來發現支配這些選擇的原則。
圖14
圖14:一個經典的伊斯蘭星形圖案,它不能很容易地使用漢金的方法和玫瑰花環變換的組合來表示。
漢金密鋪比Najm密鋪更适合制作某些圖案。邦納展示了幾個與衆不同的圖案組合;圖15顯示了11點和13點玫瑰花環的圖案。這些引人注目的設計之是以成為可能,是因為額外的一層不規則拼塊可以吸收在協調規則11-和13-多邊形的不相容角度時産生的誤差。請注意,産生此設計的密鋪不是任何密鋪的玫瑰花環變換。是以,漢金拼塊在某些情況下可以被認為是"原始的"。另一個原始的漢金密鋪是圖3最下面一行中的"Altair"密鋪。用這種方式檢查規則多邊形的其他不尋常的組合可以容納在單個圖案中,以及如何自動生成相關的漢金密鋪,這将是一件很有趣的事情。
這項工作中另一個未探索的方向是它對非歐幾裡德幾何的擴充,正如Kaplan和Salesin[18]所證明的那樣。這一擴充将是直截了當的。唯一的變化将是玫瑰變換中縮放規則多邊形的公式的一般化。應該可以用他們論文附錄中給出的"絕對三角"來表達一個一般公式。
圖15
圖15:一個不同尋常的星形圖案,複制自邦納的手稿,以11角和13角星為特色。
參考文獻
[1] S.J. Abas and A. Salman. Geometric and group theoretic methods for computer graphics studies of
Islamic symmetric patterns. Computer Graphics Forum, 11(1):43–53, 1992.
[2] S.J. Abas and A. Salman. Symmetries of Islamic Geometrical Patterns. World Scientifific, 1995.
[3] Jay Bonner. Islamic Geometric Patterns: Their Historical Development and Traditional Methods of Derivation. Unpublished, 2000.
[4] Jay Bonner. Three traditions of self-similarity in fourteenth and fifteenth century islamic geometric
ornament. In Reza Sarhangi and Nathaniel Friedman, editors, ISAMA/Bridges 2003 Proceedings,
pages 1–12, 2003.
[5] F. H. Bool, J. R. Kist, J. L. Locher, and F. Wierda. M. C. Escher: His Life and Complete Graphic
Work. Harry N. Abrams, Inc., 1992.
[6] J. Bourgoin. Arabic Geometrical Pattern and Design. Dover Publications, 1973.
[7] Jean-Marc Cast´era. Arabesques: Decorative Art in Morocco. ACR Edition, 1999.
[8] Keith Critchlow. Islamic Patterns: An Analytical and Cosmological Approach. Thames and Hudson, 1976.
[9] Franc¸ois Dispot. Arabeske home page, 2002. http://www.wozzeck.net/arabeske/index.html.
[10] Branko Grunbaum and G. C. Shephard. Tilings and Patterns. W. H. Freeman, 1987.
[11] Branko Grunbaum and G. C. Shephard. Interlace patterns in Islamic and Moorish art. Leonardo,
25:331–339, 1992.
[12] E. H. Hankin. The Drawing of Geometric Patterns in Saracenic Art, volume 15 of Memoirs of the Archaeological Society of India. Government of India, 1925.
[13] E. Hanbury Hankin. Examples of methods of drawing geometrical arabesque patterns. The Mathematical Gazette, pages 371–373, May 1925.
[14] E. Hanbury Hankin. Some diffificult Saracenic designs II. The Mathematical Gazette, pages 165–168, July 1934.
[15] E. Hanbury Hankin. Some diffificult Saracenic designs III. The Mathematical Gazette, pages 318–319, December 1936.
[16] Douglas Hofstadter. Metamagical Themas: Questing for the Essence of Mind and Pattern. Bantam Books, 1986.
[17] Craig S. Kaplan. Computer generated islamic star patterns. In Reza Sarhangi, editor, Bridges 2000 Proceedings, 2000.
[18] Craig S. Kaplan and David H. Salesin. Islamic star patterns in absolute geometry. ACM Trans. Graph., 23(2):97–119, 2004.
[19] A.J. Lee. Islamic star patterns. Muqarnas, 4:182–197, 1987.
[20] Victor Ostromoukhov. Mathematical tools for computer-generated ornamental patterns. In Electronic Publishing, Artistic Imaging and Digital Typography, number 1375 in Lecture Notes in Computer Science, pages 193–223. Springer-Verlag, 1998.
[21] Craig S. Kaplan, Islamic Star Patterns from Polygons in Contact
青山不改,綠水長流,在下告退。
轉發随意,轉載請聯系張大少本尊。