女士们,先生们,老少爷们儿们!在下张大少。
1 引言
伊斯兰星形图案代表了世界上伟大的装饰设计传统之一[2, 6, 7]。星形图案是数学、艺术和精神的和谐融合,是对称性、平衡性和独创性的表现。
星形图案还体现了一个持久的数学之谜。大部分的原始设计技术已经湮没在历史中,我们不得不通过古代工匠和数学家留下的图案来探究他们的思想。许多学者和业余爱好者已经发现或重新发现了生成伊斯兰图案的技术[1, 9, 11, 20]。
本文提出了一种基于汉金的"多边形接触法"[12]的简单技术。汉金的方法在给定平面密铺的基础上生成伊斯兰星形图案(第3节)。通过略微修改结构,我们能够按照Huff的拼花变形风格构建设计[16,第10章](第3.1节)。最后,我们展示了一个被称为"玫瑰花变换"的密铺操作如何使用汉金方法(第4节)扩展可用图案的范围。花环变换展示了汉金方法的强大功能,并形式化了某些星形图案类别之间以前无法解释的关系。
2先前的工作
我们的方法直接借鉴了Kaplan和Salesin[18]的最新研究成果。他们通过用星形图案的碎片填充拼块来构建设计。对于规则多边形的拼块,他们给出了一个参数化的"设计元素"空间,这些元素来自历史上的例子。然后他们通过使用"推理算法"填充不规则多边形来完成图案。由于他们的构造独立于欧几里得的平行公理,他们可以在欧几里得和非欧几里得的几何中无缝地绘制星形图案。我们通过消除设计元素和对所有拼块统一应用推理算法来简化他们的方法。我们仍然可以通过将更多的信息转移到底层拼块中来产生复杂的元素,如玫瑰花。这两个系统产生的设计有很大的重叠性——给定合适的拼块,Najm系统可以重现这里介绍的所有星形图案。但本文提供了对支撑星形图案的拼块的见解,并提供了一种更简单和更容易控制的技术。
Jay Bonner是一位广泛研究伊斯兰星形图案的建筑师。在一份未发表的手稿[3]中,邦纳给出了一个系统的星形图的展示,这些星形图是在巨大的密铺空间(他称之为"多边形子网格")上形成的。书中的一些技术也出现在最近的论文[4]中。Bonner的工作是作为设计师的资源,而不是软件编写人员的规范。他使用CAD工具手工绘制图案。本文在一定程度上试图将他的技术基础上的算法形式化,并将这些算法用软件表达给建筑师、设计师和艺术家。
3接触多边形方法
基于拼块的伊斯兰星形图案的方法似乎是由E.H.Hankin在20世纪初在西方提出的。在一系列的论文中[12, 13, 14, 15],他解释了他的发现并给出了许多关于如何使用该技术的例子。汉金对其技术的描述为算法方法提供了一个很好的起点(并有助于推动如今Bonner的工作)。
在制作这样的图案时,首先需要用由接触多边形组成的网络覆盖要装饰的表面。然后,通过每个多边形的每条边的中心绘制两条线。这些线相互交叉,就像字母X一样,并一直延续到它们与其他来源相似的线相遇。这样就完成了图案[12,第4页]。
从那时起,Lee[19]和Critchlow[8]等学者都提到了汉金的"多边形接触"技术。这种方法立即提出了一种将密铺图变成伊斯兰星形图案的算法。给定一个由多边形组成的平面图(汉金的 "网络"),我们把平面图边缘的中点确定为"接触点",设计将在这里诞生。我们在每个接触点放置一个小的X,然后 "生长"X的手臂,直到它们遇到从其他接触点增长的线条。在这个过程中,有一个明显的自由度:X的臂与它们所发出的边所形成的角度。我们称这个角度为图案的接触角。图1(a)中给出了一个说明。
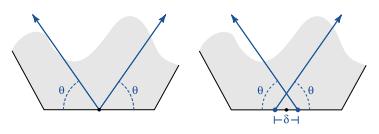
图1
图1:在汉金方法的第一步中,每个贴图上的每个接触位置都对应着一对射线。在(a)中,单个接触位置得到两条射线,每一条射线与边缘形成接触角θ。在(b)中,我们用距离δ来分离射线源。
我们可以把这个过程看作是在一个拼块中为每个独特的拼块形状生长一个小的线条排列。我们从拼块边缘的中点向内形成一对射线,形成半个X。我们把与一块拼块相关的线条的排列称为它的主题。这种构造技术的实现应该接受一个密铺和一个接触角作为输入,为每个密铺形状构建一个图案,然后将这些图案组装成一个可以装饰的图案。
给定一个正n边形拼块和一个接触角,我们必须从通过其边缘中点进入该拼块的2n条射线中开发一个图案。一个成功的图案将把射线分成几对,其中每一对匹配的射线代表了一条通过拼块的独特路径。最好的图案将是能优化所选美学目标的光线配对。我们选择了一个简单的目标:最小化图案中所有线段的长度之和。这个目标反映了伊斯兰设计中的经济性和必然性,并通过许多历史上的例子得到了证明。
那么,在理想情况下,我们将遍历所有可能的射线配对,并找到总长度最小的那个。不幸的是,这种算法并不实用——有n!(n/2)!2n种方法可以将2n条射线分割成一对,或者对于一个有10条边的区域来说,有超过5亿种可能性。
相反,我们使用一种贪婪的方法,基于Kaplan和Salesin的推理算法的简化版本[18]。我们考虑所有可能的射线对。如果两条射线→AB和→CD相交于点P,我们将这对射线存储在一个集合中,其成本等于AP和PD的长度之和。如果这两条射线是相邻的,并且相互指向对方,我们就把这一对射线和长度AD放在一起。然后我们可以按成本对集合进行排序,并按顺序走过它。对于每一对射线,只要这对射线还没有被使用过,我们就把这对射线的路径纳入图案中。
在实践中,这种算法在各种各样的多边形上表现良好。当然,它在规则多边形上的表现是完美的,它在那里构建了星形图案。它有时会产生具有不匹配射线的图案,有时会产生离底层拼块太远的路径。在它失败的情况下,通常不是因为它贪婪,而是因为配对技术不适合有关的拼块形状。在某些情况下,可以通过将接触点从边缘中点移开来改善推断的图案。第4节将更详细地讨论这种调整。
图2说明了从接触位置生长射线的过程。图3显示了一些典型的设计,这些设计可以通过使用我们对汉金方法的实施而产生。
图2
图2:汉金方法的演示。在左边,接触点生长出x形的射线排列,直到它们遇到其他射线。当原始的密铺被移除时,结果就是右边的图案。
图3
图3:使用汉金方法构建的星图示例。每一行都显示了一种密铺和三种设计,这些设计可以使用三种不同的接触角从密铺中派生出来。最下面一行的特色是由近乎规则的多边形进行的有趣的密铺。它转载自Grunbaum and Shephard[10,第64页],提醒人们过度依赖数字的危险。一个相关的设计也出现在Bourgoin[6,版图163]中。
在有些情况下,对基本推理算法的简单修改可以改善生成的图案。例如,考虑图4(a)中给出的星形图案。这个图案包含大面积的区域,来自于正十二边形,没有被填满。一个更有吸引力的图案可以通过推理算法的第二遍来构建,从第一遍推理的射线相遇的点向内构建。由此产生的设计,如图4(b)所示,与传统更加一致。在推理算法中,很容易识别出所提供的拼块形状是一个规则的多边形,并在艺术家指定的时候运行第二轮推理。Kaplan和Salesin[18]通过对可用于填充规则多边形的图案范围提供更明确的参数化来解决这个问题。
图4
图4:对推理算法的扩展可以产生一个稍微有吸引力的图案的两种情况的演示。在(a)中,一个星形图案显示了大面积的未填充区域,这些区域是原始拼块中的规则十边形的中心。在图案的内部添加一层推断的几何图形,产生了(b)中的改进设计。这个过程在(c)和(d)中用不同的拼块重复。
一个进一步的改进是允许接触位置一分为二,如图1(b)所示。分割可以通过为推理算法提供第二个实值参数δ来完成,该参数指定了射线的新起点之间的距离。参数δ可以从零(给出原始结构)到拼块中最短的拼块边缘的长度变化。这种修改可以得到Bonner所说的 "两点图案",这是一组在伊斯兰艺术中具有重要历史意义的图案[3]。使用δ参数构建的两点图案的例子显示在图5中。与两点图案相对应的设计往往是由非常短的封闭线组成的,每条封闭线都围绕着原始拼块的一个顶点形成一个环形。接触角通常选择45◦,在拼块边缘的中点周围形成正方形。
图5
图5:用汉金的方法构造的两点星形图案的例子。每一行显示了一个模板拼块,一个δ=0的星形图案,以及一个δ非零的相关两点图案。
伊斯兰拼花变形
拼花变形是一种装饰设计风格,由威廉-赫夫创造,后来由侯世达[16,第10章]推广。它们是一种"空间动画",一种在空间而不是时间上进行平滑过渡的几何图形。拼花变形与M.C.埃舍尔的变形版画[5,第280页]密切相关,尽管与埃舍尔的作品不同,它们是纯粹的抽象几何构成。
利用汉金的方法,我们可以引入一种新的伊斯兰设计风格,我们称之为"伊斯兰镶木地板变形"。我们简单地修改推理算法,使接触角沿着一条线变化。一条射线的接触角是根据该射线的起始位置的水平位置的函数来选择的。这样一来,离开一个给定的接触位置的四条射线仍然形成一个X,即使接触角在一个单一的拼块内可能有所不同。
接触角的平滑变化导致了轻微变化的几何设计,仍然可以辨认出伊斯兰风格(参见图6)。我们认为,这些镶木地板变形在伊斯兰几何艺术世界中占据了一个有趣的位置。这种结构在伊斯兰传统中是显而易见的,但它们不会在历史上产生,因为几乎没有重复。手工绘制出不断变化的形状,然后执行它们的工作,会考验昔日工匠的耐心。
图6
图6:基于汉金方法的伊斯兰拼花变形。上图显示了根据射线起点的水平位置不断改变射线的接触角的效果。当这个过程被带到所有其他的拼块上时,中间的设计就出现了。在这个设计中,接触角从侧面的最小22.5◦到中间的67.5◦不等。在底部的设计中,接触角从两侧的36◦到中间的72◦不等。
4 .玫瑰花变换
汉金接触多边形法的一个奇特特性是,在适当的接触角选择下,不同的密铺可能产生相同的星形图案。图7中最上面一行的图案就是一个例子。它可以产生的拼块在左边使用54°的接触角,在右边使用36◦的接触角。因此,我们可能会怀疑这两个拼块之间的关系。
图7
图7:不同的拼块可以产生相同的伊斯兰设计的例子。在两种情况下,左边的密铺都是使用设计元素和推理的组合来填充的,而右边的密铺则单独使用推理。他们在中心的共享设计中相遇。
这种关系的进一步证据可以在Kaplan和Salesin[18]的Najm系统产生的星形图案中找到。图7的底排显示了左边的拼块,其"玫瑰花"图案放置在规则的十边形中。Kaplan和salesin提供了这些玫瑰花的明确参数化。但是图的右边展示了同样的图案可以通过推理单独从表面上相关的拼块中产生。
我们对汉金方法的经验表明,有许多对拼块以这种方式相关。参照图7,我们将左边的密铺称为"Najm密铺",将右边的密铺称为"汉金密铺"。这两个有相似的结构,除了在汉金拼块大的正多边形是由潜在的不规则多边形,通常是五边形的环分开。
在他的手稿[3]中,邦纳使用了这两种拼贴来创造星形图案,他也观察到一个单一的设计可能源于多个拼贴。在本节中,我们将介绍一种称为"玫瑰变换"的密铺变换,它解释了Najm密铺和汉金密铺之间的联系。我们还将我们的方法与Najm的方法进行了比较,即每种方法都能产生的图案。
玫瑰变换的算法让人联想到第3节中使用的推理算法。给定一个拼块,它为每个不同的拼块形状构造一个平面图。然后,这些平面图被组装起来,这次是组装成一个新的拼块,而不是一个最终设计。这也是一种二元化:最常见的操作是将垂直平分线竖立到原始拼块的边上。每个拼块形状的图纸是以两种方式之一构建的。
正多边形。如果拼块是半径为r的正n边形P,且具有五条或更多边,则贴图的构造如图8所示。我们构建一个半径为R0<r的新正则n-多边形P0,并将其放置在与原始多边形同心但相对于其旋转π/n的位置。然后,我们添加连接P0的顶点和P的边中点的线段。选择内半径R0是为了使这些新线段中的每一条的长度正好是P0边长的一半。一些三角学表明,给定n和r,r0的正确值由下式给出
返回的图纸是P0以及连接它到P的边缘中点的线段。
图8
图8:应用于正多边形的玫瑰花形变换。这里,半径为r的正10边形填充了半径为r0的较小的正10边形,以及将内多边形的顶点连接到外多边形的边中点的线段。选择内径是为了使标记的边具有相同的长度。
不规则多边形。如果拼块是一个不满足上述条件的多边形P,我们将P的边的垂直平分线向其内部延伸,如图9所示。在它们相交的地方截断分界线。其结果成为这块拼块的图纸。
图9
图9:应用于不规则多边形的玫瑰花环变换。在左侧,将为每条拼块边缘绘制一条垂直平分线,作为指向拼块内部的射线。与推理算法一样,射线在彼此相遇时会被截断。
这一步在实质上类似于90◦接触角的推理算法。我们不期望它对每一个可能的多边形都返回一个有意义的答案,但是在Najm拼块中出现的多边形的情况下,它发现的图纸通常是合适的。
一些启发式算法在这里也起作用,但在推理算法中并不适用。一个适度成功的启发式方法是考虑所有成对射线的交点,并对位于拼块内的那些点进行聚类。然后,每个聚类可以被平均到一个点上,所有对该聚类有贡献的射线都可以将其作为端点。这种调整可能会使一些射线偏离垂直方向,从而在转换后的拼块边缘的中间位置引入"扭结"。我们可以在以后通过检测结点并将其替换为直线段来纠正这个问题。
当此算法在Najm密铺上运行时,它倾向于生成汉金密铺。例如,图8和图9中的两个密铺对应于图7左侧的Najm密铺。玫瑰变换在图的右侧生成汉金密铺。图10给出了另外两个密铺及其玫瑰花形转换的示例。
图10
图10:玫瑰花结转换的两个演示。转换后的密铺显示为粗体叠加在原始密铺上。
玫瑰花变换将卡普兰和Salesin的"设计元素"中的智慧提取出来,并将其嵌入到拼块中。假设在给定的密铺中,Najm用于用玫瑰花环填充正多边形P。在该密铺的玫瑰花环变换中,P的缩小副本P0将被不规则五边形的环包围。用我们的方法,这些五角形将合力形成围绕在P0内的一颗中心恒星周围的六角形花环。玫瑰花环变换的动机(并以此命名)的目标是使五边形尽可能地接近规则,产生的玫瑰花环在Lee[19]给出的意义上几乎是理想的。
在某些情况下,汉金的方法在应用于玫瑰花环变换的拼块时会产生不令人满意的图案。图11显示了一个示例,其中汉金的方法发现了正确图案的拓扑,但生成了不均匀的玫瑰花环。邦纳讨论了如何在必要时通过调整五边形上远离中心的接触位置来纠正这种情况。然而,他没有给出何时或如何进行这一调整的迹象。
图11
图11:汉金的方法生成不完美的玫瑰花环的一个例子。在(A)中,Najm被用来在正八角形内放置完美的玫瑰花环。当汉金的方法用于(B)中的玫瑰花环变换时,玫瑰花环六边形(以阴影显示)有两种不同的大小。
我们可以求助于拼块和它们的花环变换之间的关系来解开这个谜团。图11(A)的设计是使用Najm方法构建的。我们选择玫瑰花来填充常规的八边形拼块。根据设计,玫瑰花环的六边形手臂(其中两个在图中显示为阴影)与其周围八边形的边缘接触。
在图11(B)中,玫瑰花臂是由在玫瑰花环变换中引入的五边形环形成的。其中一个五边形的结构如图12所示。问题是AE和BE的长度不同。如果我们简单地将接触位置放置在边缘中点,则沿边AB和CD的接触位置与其相邻八角形的中心的距离不相等,从而产生不均匀的玫瑰花臂排列。尽管着色的五边形在拓扑上与其包含的顶点是对偶的,但它不是对偶的(其边不会被原始密铺一分为二)。我们通过记录玫瑰花变换与原始拼贴的交点,并将它们作为接触位置来纠正这种差异。
图12
图12:汉金方法中恢复完美花环的接触位置调整的图解。水平线表示玫瑰花变换中着色拼块边缘的中点。但是接触点的正确位置是该边与原始密铺的边的交点。
因此,这两种密铺之间存在着深刻的联系,这可能会暴露出看似武断但必要的调整背后的逻辑。此外,在计算玫瑰花环变换时,这些修正的接触位置可以很容易地计算出来。
5 实施
我们已经将本文描述的方法作为一个独立的Java应用程序来实现。该应用程序的界面显示了一个叠加了相应伊斯兰星形图案的拼块。用户能够选择要使用的拼块,并修改用于产生两点图案的接触角θ和距离δ。他们还可以选择是否在大型规则多边形中加入推理算法的第二遍,以及是否如第4节末尾所述调整远离边缘中点的接触位置。所有这些变化都以交互方式反映在设计中,使得浏览各种星形图案变得容易和愉快。当用户决定了一个设计后,他们可以使用首先为Taprats[17]开发的装饰风格来渲染它。图13中显示了一个装饰的图案。
图13
图13:使用接触多边形方法制作的装饰星形图案
我们目前的软件只处理周期性的密铺(尽管在基础技术中没有这种限制)。一个密铺是由两个平移向量和一个未变换的多边形集合表示的。每个多边形都有一个变换列表,将其地图到单一平移单元中的出现。这些信息足以用密铺的一个子集来覆盖平面的任何区域。在交互式设计器中,代表图案的平面图与拼块形状相关,并与它们一起绘制。一个独立的Java应用程序可以用来手工构建周期性的拼块。用户可以创建规则的多边形拼块并将它们扣在一起,用新的拼块填充不规则的孔,并指定平移矢量。另一个程序接受周期性密铺作为输入,并计算其玫瑰花形变换。
伊斯兰拼花地板变形的构建需要多次单独调用推理算法,目前速度太慢,无法交互运行。它是作为命令行应用程序实现的,该应用程序根据指定边界框和接触角度范围的参数构建设计。
6未来工作
尽管汉金的方法结合了玫瑰花环变换的力量,但一些重要的历史模式仍然遥不可及。图14中给出了一个例子。使用Kaplan和Salesin的Najm可以很容易地从十二边形和三角形的密铺中构建该图案。他们的技术为十二角形中的图案提供了一种明确的参数化,他们称之为"扩展花环"。人们很容易认为,我们可以通过在此密铺上进行两次玫瑰花环变换迭代来获得相同的模式。仔细观察发现,在直线相交的地方,它们形成30◦和60◦的角。此图案的任何基于推理的表示都需要允许多个不同的接触角,或者在推理算法中进行非贪婪选择。无论哪种方式,都需要更多的工作来发现支配这些选择的原则。
图14
图14:一个经典的伊斯兰星形图案,它不能很容易地使用汉金的方法和玫瑰花环变换的组合来表示。
汉金密铺比Najm密铺更适合制作某些图案。邦纳展示了几个与众不同的图案组合;图15显示了11点和13点玫瑰花环的图案。这些引人注目的设计之所以成为可能,是因为额外的一层不规则拼块可以吸收在协调规则11-和13-多边形的不相容角度时产生的误差。请注意,产生此设计的密铺不是任何密铺的玫瑰花环变换。因此,汉金拼块在某些情况下可以被认为是"原始的"。另一个原始的汉金密铺是图3最下面一行中的"Altair"密铺。用这种方式检查规则多边形的其他不寻常的组合可以容纳在单个图案中,以及如何自动生成相关的汉金密铺,这将是一件很有趣的事情。
这项工作中另一个未探索的方向是它对非欧几里德几何的扩展,正如Kaplan和Salesin[18]所证明的那样。这一扩展将是直截了当的。唯一的变化将是玫瑰变换中缩放规则多边形的公式的一般化。应该可以用他们论文附录中给出的"绝对三角"来表达一个一般公式。
图15
图15:一个不同寻常的星形图案,复制自邦纳的手稿,以11角和13角星为特色。
参考文献
[1] S.J. Abas and A. Salman. Geometric and group theoretic methods for computer graphics studies of
Islamic symmetric patterns. Computer Graphics Forum, 11(1):43–53, 1992.
[2] S.J. Abas and A. Salman. Symmetries of Islamic Geometrical Patterns. World Scientifific, 1995.
[3] Jay Bonner. Islamic Geometric Patterns: Their Historical Development and Traditional Methods of Derivation. Unpublished, 2000.
[4] Jay Bonner. Three traditions of self-similarity in fourteenth and fifteenth century islamic geometric
ornament. In Reza Sarhangi and Nathaniel Friedman, editors, ISAMA/Bridges 2003 Proceedings,
pages 1–12, 2003.
[5] F. H. Bool, J. R. Kist, J. L. Locher, and F. Wierda. M. C. Escher: His Life and Complete Graphic
Work. Harry N. Abrams, Inc., 1992.
[6] J. Bourgoin. Arabic Geometrical Pattern and Design. Dover Publications, 1973.
[7] Jean-Marc Cast´era. Arabesques: Decorative Art in Morocco. ACR Edition, 1999.
[8] Keith Critchlow. Islamic Patterns: An Analytical and Cosmological Approach. Thames and Hudson, 1976.
[9] Franc¸ois Dispot. Arabeske home page, 2002. http://www.wozzeck.net/arabeske/index.html.
[10] Branko Grunbaum and G. C. Shephard. Tilings and Patterns. W. H. Freeman, 1987.
[11] Branko Grunbaum and G. C. Shephard. Interlace patterns in Islamic and Moorish art. Leonardo,
25:331–339, 1992.
[12] E. H. Hankin. The Drawing of Geometric Patterns in Saracenic Art, volume 15 of Memoirs of the Archaeological Society of India. Government of India, 1925.
[13] E. Hanbury Hankin. Examples of methods of drawing geometrical arabesque patterns. The Mathematical Gazette, pages 371–373, May 1925.
[14] E. Hanbury Hankin. Some diffificult Saracenic designs II. The Mathematical Gazette, pages 165–168, July 1934.
[15] E. Hanbury Hankin. Some diffificult Saracenic designs III. The Mathematical Gazette, pages 318–319, December 1936.
[16] Douglas Hofstadter. Metamagical Themas: Questing for the Essence of Mind and Pattern. Bantam Books, 1986.
[17] Craig S. Kaplan. Computer generated islamic star patterns. In Reza Sarhangi, editor, Bridges 2000 Proceedings, 2000.
[18] Craig S. Kaplan and David H. Salesin. Islamic star patterns in absolute geometry. ACM Trans. Graph., 23(2):97–119, 2004.
[19] A.J. Lee. Islamic star patterns. Muqarnas, 4:182–197, 1987.
[20] Victor Ostromoukhov. Mathematical tools for computer-generated ornamental patterns. In Electronic Publishing, Artistic Imaging and Digital Typography, number 1375 in Lecture Notes in Computer Science, pages 193–223. Springer-Verlag, 1998.
[21] Craig S. Kaplan, Islamic Star Patterns from Polygons in Contact
青山不改,绿水长流,在下告退。
转发随意,转载请联系张大少本尊。