切比雪夫多項式是與棣美弗定理有關,以遞歸方式定義的一系列正交多項式序列。 通常,第一類切比雪夫多項式以符号Tn表示, 第二類切比雪夫多項式用Un表示。切比雪夫多項式 Tn 或 Un 代表 n 階多項式。
切比雪夫多項式在逼近理論中有重要的應用。這是因為第一類切比雪夫多項式的根(被稱為切比雪夫節點)可以用于多項式插值。相應的插值多項式能最大限度地降低龍格現象,并且提供多項式在連續函數的最佳一緻逼近。
對每個非負整數n, Tn(x) 和 Un(x) 都為 n次多項式。 并且當n為偶(奇)數時,它們是關于x 的偶(奇)函數, 在寫成關于x的多項式時隻有偶(奇)次項。
按切比雪夫多項式的展開式:
一個N 次多項式按切比雪夫多項式的展開式為如下,多項式按切比雪夫多項式的展開可以用 Clenshaw 遞推公式計算。第一類切比雪夫多項式由以下遞推關系确定。
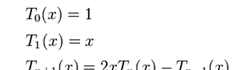
也可以用母函數表示。
第二類切比雪夫多項式 由以下遞推關系給出。
此時母函數為
在數值分析中,Clenshaw遞推公式 (由Charles William Clenshaw發現)是一個求切比雪夫多項式的值的遞歸方法。
N次切比雪夫多項式,是下面形式的多項式p(x)
其中Tn是n階切比雪夫多項式
Clenshaw遞推公式可以用來計算切比雪夫多項式的值。給定
我們定義
于是
(注)上面的公式在 N=0,1的情況下無意義。此時我們可以用下面的公式:
(downward, omit if N=0)
這裡
或者
其中
是第二類切比雪夫多項式
設兩個複數(用三角形式表示)Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),則:
Z1Z2=r1r2[cos(θ1+θ2)+isin(θ1+θ2)].
證:先講一下複數的三角形式的概念。在複平面C上,用向量Z(a,b)來表示Z=a+bi.于是,該向量可以分成兩個在實軸,虛軸上的分向量.如果向量Z與實軸的夾角為θ,這兩個分向量的模分别等于rcosθ,risinθ(r=√a^2+b^2).是以,複數Z可以表示為Z=r(cosθ+isinθ).這裡θ稱為複數Z的輻角.
因為Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),是以
Z1Z2=r1r2(cosθ1+isinθ1)(cosθ2+isinθ2)
=r1r2(cosθ1cosθ2+icosθ1sinθ2+isinθ1cosθ2-sinθ1sinθ2)
=r1r2[(cosθ1cosθ2-sinθ1sinθ2)+i(cosθ1sinθ2+sinθ1cosθ2)]
=r1r2[cos(θ1+θ2)+isin(θ1+θ2)].
其實該定理可以推廣為一般形式:
設n個複數Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),……,Zn=rn(cosθn+isinθn),則:
Z1Z2……Zn=r1r2……rn[cos(θ1+θ2+……+θn)+isin(θ1+θ2+……+θn)].
證:用數學歸納法即可,歸納基礎就是兩個複數相乘的棣莫弗定理。
如果把棣莫弗定理和歐拉(Euler)公式“e^iθ=cosθ+isinθ”(參見《泰勒公式》,嚴格的證明需要複分析)放在一起看,則可以用來了解歐拉公式的意義。
利用棣莫弗定理有:
Z1Z2……Zn=r1r2……rn [cos(θ1+θ2+……+θn)+isin(θ1+θ2+……+θn)]
如果可以把所有的複數改寫成指數的形式,即:Z1=r1e^iθ1,Z2=r2e^iθ2,……,Zn=rne^iθn,
Z1Z2……Zn=r1r2……rn e^i(θ1+θ2+……+θn)
這和指數的可加性一緻.
在一般形式中如果令Z1=Z2=……=Zn=Z,則能導出複數開方的公式.有興趣可自己推推看.
下面這題可作為切比雪夫多項式的模版:
TimeLimit: 2000/1000 MS (Java/Others) Memory Limit:32768/32768 K (Java/Others)
Total Submission(s): 714 Accepted Submission(s): 206
Problem Description
f(cos(x))=cos(n∗x) holds for all x.
Given two integersn and m , you need to calculate the coefficient of x^m in f(x), modulo 998244353
Input
Multiple testcases (no more than 100).
Each test casecontains one line consisting of two integers n and m.
1≤n≤109,0≤m≤104
Output
Output the answerin a single line for each test case.
Sample Input
2 0
2 1
2 2
Sample Output
998244352
2
【題意】
給出一個函數,代入n,m後求出xm的系數,并取模輸出。
【思路】
我們先嘗試把cos(nx)化為cos(x)的形式,然後把cos(x)用x代換,就可以得到f(x)=...的形式,然後就能得到所求的系數了。
那麼我們如何把cos(nx)化為cos(x)的形式呢。
其實可以嘗試着暴力寫出前幾項的形式。如下圖:
由寫出的式子,我們可以發現以下幾點:
當m大于n時,答案顯然為0。
當n為奇數且m為偶數或n為偶數且m為奇數時答案顯然為0。
當n為奇數,且m為1時,答案的絕對值為n。
當n為偶數,且m為0時,答案的絕對值為1。
其餘情況答案的絕對值均為【 n * (n-m+2) * (n-m+4) * ... * (n+m-4) * (n+m-2) 】/(m!)。(注意逆元的運用)
上面出現絕對值的情況,3和4 當(n/2)%2 == 0 時符号為正,否則為負;5 當((n-m)/2)%2 == 0時,符号為正,否則符号為負。
依照這個規律分類讨論一下即可。
于是我們可以得到以下一般解析式
注意"!!"不是階乘的階乘,而是不超過n且與n具有相同奇偶性的所有正整數連乘積。
n分類讨論下,當n為偶數時m=2*k, n為奇數時m=2*k-1
還有注意下"!!"的約分,可能下面的比上面的大
于是我們就得到了以下代碼: