本节书摘来自异步社区出版社《matlab智能算法超级学习手册》一书中的第2章,第2.2节,作者:matlab技术联盟 , 高飞 , 许玢更多章节内容可以访问云栖社区“异步社区”公众号查看。
matlab智能算法超级学习手册
蓝鲸和长须鲸是两个生活在同一海域的相似的种群,因此认为它们之间存在竞争。估计蓝鲸的固有增长率每年为5%,长须鲸为每年8%。估计蓝鲸环境承载力(环境能够支持的鲸鱼的最大数量)为150 000条,长须鲸为400 000条。鲸鱼竞争的程度是未知的。过去约100年剧烈的捕捞已经使鲸鱼数量减少,蓝鲸大约5 000条,长须鲸大约70 000条。蓝鲸是否会灭绝?
解:该问题是对2.1节第(1)、(2)、(3)问的具体化。根据实际统计数据,进行蓝鲸和长须鲸的种群竞争模型模拟计算。假设蓝鲸和长须鲸的增长情况仅与两者之间的竞争有关,与其他动物无关;不考虑环境改变带来的影响,环境承载力是稳定的;人类停止对鲸鱼的捕杀,鲸鱼按自然条件繁衍。
建立相应的数学模型:
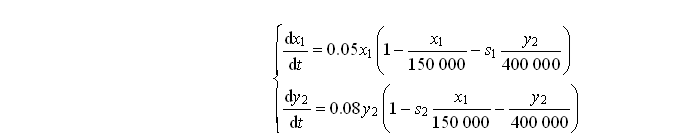
由于蓝鲸和长须鲸的竞争是未知的,根据实际情况,当s 1、s 2取2时,种群间的相互影响已经非常大,所以估计s 1、s 2的区间均为(0,2)时,就可以很好地模拟实际情况。以0.1为步长,采用穷列举法,代入不同的s 1、s 2,求出最后蓝鲸与长须鲸的稳定状态数值。求解的图形如图2-8、图2-9所示。
不同情况下s 1、s 2的具体数值列表如下。
由以上三表所示结果可知,由于蓝鲸的固有增长率每年为5%,长须鲸为每年8%,蓝鲸环境承载力为150 000条,长须鲸为400 000条,所以长须鲸在相同的竞争程度条件下明显具有一定的优势。因而,当蓝鲸具有优势,最后稳态值为x=150000,y=0时的要s 1、s 2必定是s 2较大、s 1较小,而表2-2中s 1基本小于1、s 2基本大于1,正好体现了在蓝鲸对长须鲸影响小、蓝鲸对长须鲸影响大的条件下,蓝鲸具有优势的实际情况。
同样,当长须鲸具有优势,最后稳态值为x=0,y=400000时,根据实际,必然是s1较大(s 1>1),而s2较小(s2<1);同时,由于长须鲸本身对环境的适应力较强(体现在增长率和环境承载力较大),所以即使在相互抑制作用均较大(s1,s 2>1)时,仍然是长须鲸处于优势地位。综合所述,s 1>1时,无论s 2取何值,长须鲸都具有优势。表2-3中,s 1在1.1以上时,x=0,说明理论计算结果很好地符合实际情况。
通过以上分析可知,蓝鲸不一定毁灭,s 1、s 2的取值不同时,最后的稳定状态不同。
种群函数:
主程序:
当s 1、s 2改变时,蓝鲸与长须鲸的量数: