题目描述:
题目背景: NOIP2011 DAY2 试题 2 。
小T是一名质量监督员,最近负责检验一批矿产的质量。这批矿产共有 n 个矿石,从 1 到 n 逐一编号,每个矿石都有自己的重量 wi 以及价值 vi。检验矿产的流程是:
1、给定 m 个区间[Li,Ri];
2、选出一个参数 W ;
3、对于一个区间[Li,Ri],计算矿石在这个区间上的检验值 Yi:
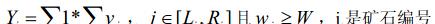
这批矿产的检验结果Y 为各个区间的检验值之和。即:
若这批矿产的检验结果与所给标准值 S 相差太多,就需要再去检验另一批矿产。小 T 不想费时间去检验另一批矿产,所以他想通过调整参数 W 的值,让检验结果尽可能的靠近标准值 S ,即使得 S-Y 的绝对值最小。请你帮忙求出这个最小值。
输入格式:
第一行包含三个整数 n,m,S,分别表示矿石的个数、区间的个数和标准值。
接下来的 n 行,每行 2 个整数,中间用空格隔开,第 i+1 行表示 i 号矿石的重量 wi 和价值 vi 。
接下来的 m 行,表示区间,每行 2 个整数,中间用空格隔开,第 i+n+1 行表示区间 [Li,Ri] 的两个端点 Li 和 Ri。注意:不同区间可能重合或相互重叠。
输出格式:
输出只有一行,包含一个整数,表示所求的最小值。
样例输入:
5 3 15
1 5
2 5
3 5
4 5
5 5
1 5
2 4
3 3
样例输出:
10
备注:
样例说明:当 W 选 4 的时候,三个区间上检验值分别为 20、5、0,这批矿产的检验结果为 25,此时与标准值 S 相差最小为 10 。
数据范围:
对于 10% 的数据,有 1≤n,m≤10;
对于 30% 的数据,有 1≤n,m≤500;
对于 50% 的数据,有 1≤n,m≤5,000;
对于 70% 的数据,有 1≤n,m≤10,000;
对于 100% 的数据,有 1≤n,m≤200,000;0<wi,vi≤106;0<S≤1012;1≤Li≤Ri≤n。
题目分析:
二分法。表示看不懂第一个求和,后来问了别人才知道是满足要求的个数。就直接二分w,显然w越大,计算出来的y越小。如果计算出来的y大于了s,就把w变大,反之,把w变小。
附代码:
#include<iostream>
#include<cstring>
#include<string>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<ctime>
#include<set>
#include<queue>
#include<map>
#include<map>
#include<iomanip>
#include<algorithm>
using namespace std;
const int maxn=+;
int n,m,num[maxn],w[maxn],v[maxn],l[maxn],r[maxn];
long long sum[maxn],ans,s;
int readint()
{
char ch;int i=,f=;
for(ch=getchar();(ch<'0'||ch>'9')&&ch!='-';ch=getchar());
if(ch=='-') {ch=getchar();f=-;}
for(;ch>='0'&&ch<='9';ch=getchar()) i=(i<<)+(i<<)+ch-'0';
return i*f;
}
long long check(int x)
{
memset(num,,sizeof(num));
memset(sum,,sizeof(sum));
ans=;
for(int i=;i<=n;i++)
{
num[i]=num[i-];
if(w[i]>=x) num[i]++;
sum[i]=sum[i-];
if(w[i]>=x) sum[i]+=v[i];
}
for(int i=;i<=m;i++)
ans+=((num[r[i]]-num[l[i]-])*(sum[r[i]]-sum[l[i]-]));
return ans;
}
long long half()
{
int l=,r=,mid;
long long ret,ret1,ret2,ret3;
while(l<=r)
{
mid=(l+r)>>;
ret=check(mid);
if(ret==s) break;
if(ret>s)
l=mid+;
else
r=mid-;
}
if(ret==s) return ret;
ret1=check(l);ret2=check(r);
if(abs(ret1-s)<=abs(ret2-s)) return ret1;//因为最后l,r会是一大一小,但谁离s近并不确定,需要判断。
if(abs(ret2-s)<=abs(ret1-s)) return ret2;
}
int main()
{
//freopen("lx.in","r",stdin);
n=readint();m=readint();scanf("%I64d",&s);
for(int i=;i<=n;i++)
{
w[i]=readint();
v[i]=readint();
}
for(int i=;i<=m;i++)
{
l[i]=readint();
r[i]=readint();
}
printf("%I64d",abs(half()-s));
return ;
}