例题一览（可看着这些题目想出来代码才算过关）

（全程注意封装，养成良好的面向对象思维）

害死人不偿命的（3n+1）猜想（卡拉兹幻想）
挖掘机技术哪家强
A+B和C
A+B and C（64Bit）
部分A+B
程序运行时间
划拳
数组元素循环右移问题
数字分类
锤子剪子布
Shuffling Machine
Shortest Distance
一元多项式求导
A+B for Polynomials
Product of Polynomials

害死人不偿命的（3n+1）猜想（卡拉兹幻想）

输入一个数，偶数时则砍掉一半；奇数时，则（3n+1）砍掉一半，最后直到得到1.

问，进行了多少次？

挖掘机技术哪家强

题目描述

为了用事实说明挖据机技术到底哪家强,PAT组织了一场挖据机技能大赛。请根据比赛结果统计出技术最强的那个学校。

输入格式

在第1行给出不超过10的正整数N,即参赛人数。随后N行,每行给出一位参赛者的信息和成绩,包括其所代表的学校的编号(从1开始连续编号)及其比赛成绩(百分制),中间以空格分隔。

输出格式

在一行中给出总得分最高的学校的编号及其总分,中间以空格分隔。题目保证答案唯一,没有并列。

输入样例

3 65

2 80

1 100

2 70

3 40

3 0

输出样例

2 150

A+B和C

题目描述

给定区间 [−2^31,2^31] 内的 3 个整数 A、B 和 C，请判断 A+B 是否大于 C。

输入格式：

输入第 1 行给出正整数 T (≤10)，是测试用例的个数。随后给出 T 组测试用例，每组占一行，顺序给出 A、B和 C。整数间以空格分隔。

输出格式：

对每组测试用例，在一行中输出 Case #X: true 如果 A+B>C，否则输出 Case #X: false，其中 X 是测试用例的编号（从 1 开始）。

1 2 3

2 3 4

2147483647 0 2147483646

0 -2147483648 -2147483647

A+B and C（64Bit）

给定 [− 2^63,2^63]中的三个整数A，B和C，您应该确定是否A + B> C。

输入规格：

输入的第一行给出测试用例的正数T（≤10）。然后是T个测试用例，每个用例包含一行，其中包含三个整数A，B和C，以单个空格分隔。

输出规格：

对于每个测试用例，在一行中输出情况#X：如果A + B> C，则为true

A + B> C或KaTeX解析错误：预期为'EOF'，在位置6获得'＃'：案例＃̲X：否则为false，其中X为案例编号（从1开始）。

Sample Input:

3

1 2 3

2 3 4

9223372036854775807 -9223372036854775808 0

复制

Sample Output:

Case #1: false

    Case #2: true

    Case #3: false

复制

部分A+B

正整数A的“DA（为1位整数）部分”定义为由A中所有DA组成的新整数PA。例如：给定A = 3862767，DA = 6，则A的“6部分”PA是66，因为A中有2个6。

现给定A、DA、B、DB，请编写程序计算PA + PB。

输入格式：

输入在一行中依次给出A、DA、B、DB，中间以空格分隔，其中0 < A, B < 10^10。

输出格式：

在一行中输出PA + PB的值。

输入样例1：

3862767 6 13530293 3

输出样例1：

399

程序运行时间

要获得一个C语言程序的运行时间，常用的方法是调用头文件time.h，其中提供了clock()函数，可以捕捉从程序开始运行到clock()被调用时所耗费的时间。这个时间单位是clock tick，即“时钟打点”。同时还有一个常数CLK_TCK，给出了机器时钟每秒所走的时钟打点数。于是为了获得一个函数f的运行时间，我们只要在调用f之前先调用clock()，获得一个时钟打点数C1；在f执行完成后再调用clock()，获得另一个时钟打点数C2；两次获得的时钟打点数之差(C2-C1)就是f运行所消耗的时钟打点数，再除以常数CLK_TCK，就得到了以秒为单位的运行时间。这里不妨简单假设常数CLK_TCK为100。现给定被测函数前后两次获得的时钟打点数，请你给出被测函数运行的时间。

输入格式：

输入在一行中顺序给出2个整数C1和C1。注意两次获得的时钟打点数肯定不相同，即C1 < C2，并且取值在[0, 10^7]。

输出格式：

在一行中输出被测函数运行的时间。运行时间必须按照“hh:mm:ss”（即2位的“时:分:秒”）

格式输出；不足1秒的时间四舍五入到秒。

输入样例：

123 4577973

输出样例：

12:42:59

划拳

划拳是古老中国酒文化的一个有趣的组成部分。酒桌上两人划拳的方法为：每人口中喊出一个数字，同时用手比划出一个数字。如果谁比划出的数字正好等于两人喊出的数字之和，谁就赢了，输家罚一杯酒。两人同赢或两人同输则继续下一轮，直到唯一的赢家出现。

下面给出甲、乙两人的划拳记录，请你统计他们最后分别喝了多少杯酒。

输入格式：

输入第一行先给出一个正整数N（<=100），随后N行，每行给出一轮划拳的记录，格式为：

甲喊甲划乙喊乙划

其中“喊”是喊出的数字，“划”是划出的数字，均为不超过100的正整数（两只手一起划）。

输出格式：

在一行中先后输出甲、乙两人喝酒的杯数，其间以一个空格分隔。

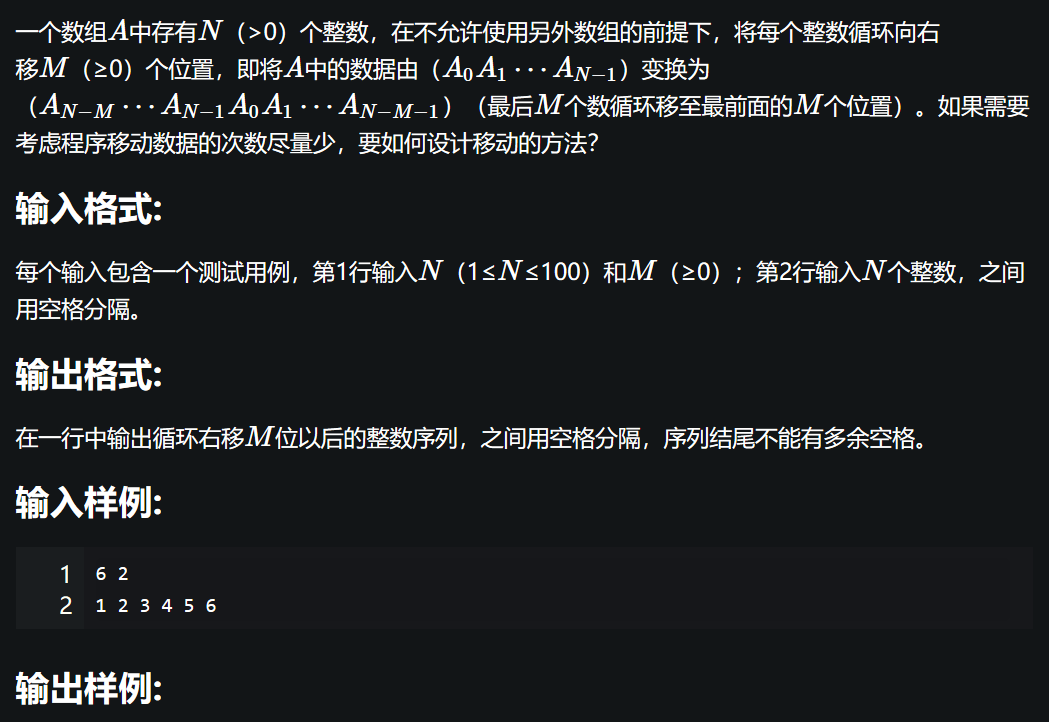
数组元素循环右移问题

数字分类

给定一系列正整数，请按要求对数字进行分类，并输出以下5个数字：

A1 = 能被5整除的数字中所有偶数的和；

A2 = 将被5除后余1的数字按给出顺序进行交错求和，即计算n1-n2+n3-n4...；

A3 = 被5除后余2的数字的个数；

A4 = 被5除后余3的数字的平均数，精确到小数点后1位；

A5 = 被5除后余4的数字中最大数字。

输入格式：

每个输入包含1个测试用例。每个测试用例先给出一个不超过1000的正整数N，随后给出N个不超过1000的待分类的正整数。数字间以空格分隔。

输出格式：

对给定的N个正整数，按题目要求计算A1~A5并在一行中顺序输出。数字间以空格分隔，但行末不得有多余空格。

若其中某一类数字不存在，则在相应位置输出“N”。

输入样例1：

13 1 2 3 4 5 6 7 8 9 10 20 16 18

输出样例1：

30 11 2 9.7 9

输入样例2：

8 1 2 4 5 6 7 9 16

输出样例2：

N 11 2 N 9

锤子剪子布

大家应该都会玩“锤子剪刀布”的游戏：两人同时给出手势，胜负规则如图所示：现给出两人的交锋记录，请统计双方的胜、平、负次数，并且给出双方分别出什么手势的胜算最大。

输入格式：

输入第1行给出正整数N（<=105），即双方交锋的次数。随后N行，每行给出一次交锋的信息，即甲、乙双方同时给出的的手势。C代表“锤子”、J代表“剪刀”、B代表“布”，第1个字母代表甲方，第2个代表乙方，中间有1个空格。

输出格式：

输出第1、2行分别给出甲、乙的胜、平、负次数，数字间以1个空格分隔。第3行给出两个字母，分别代表甲、乙获胜次数最多的手势，中间有1个空格。如果解不唯一，则输出按字母序最小的解。

输入样例：

C J

J B

C B

B B

B C

C C

C B

J B

B C

J J

输出样例：

5 3 2

2 3 5

B B

Shuffling Machine

Shortest Distance

(挖坑，待解决)

题目的意思是，有一些环形站点，给你这几个站点和邻居之间的距离，然后给你两个站点编号，求它们的最近距离。

很多种方法

第一种是顺着思路，正着搜一遍，反着搜一遍。遇到列表尾巴了就移到0,相当于环形了。优点是直观方便。

第二种是，直接把原来的距离数组复制一遍，然后就搜两次，一次从原来的begin和end搜，一次搜end到distance + begin 的距离。优点是代码少。缺点是空间复杂度高且算法没什么本质上的卵用。

还有一种是动态规划法。

既然题目已经提示有多次查询，那么把以前的计算记录存储起来就很自然。

方法是，开一个二维数组dp，对于dp[i][j]的含义就是，从i车站沿车站号增大的方向到车站j所需要的路程。比如dp[2][3]表示从车站2开到车站3的路程，而dp[3][2]就是从车站3开到最后一个车站绕回第0车站再开到车站2的路程。

我们初始化dp数组都是0

然后读入数据

遍历车站号，从0到总车站

这个车站到下一个车站的距离就是读入的数据。下一个车站用(i+1)% len(stations) 这样的取余的方式，可以规避最后加一要回到原点的问题。

接下来按照距离遍历，因为自己和自己的距离是0,自己和下一个车站的距离已经给出，所以距离从2遍历到车站数量-1

每次车站i到车站j的距离就相当于车站i到车站j-1加上车站j-1到车站j的距离。这是状态转移公式。因为是按照距离从小到大计算的，所以等号右边的一定是已经计算过的。同时用老方法规避回到起点的问题。写成代码就是

dp[j][(j + i) % len(dis)] = dp[j][(j + i - 1) % len(dis)] + dp[(j + i - 1) % len(dis)][(j + i) % len(dis)]

其中，i是遍历的距离

输出的时候取dp[i][j]与dp[j][i]的较小值即可。

以上三种方法都没有利用到一个信息。

就是整个环的长度都是固定的，假设为S，那么正着走距离是A，反着走距离一定是S-A

所以算完正的就没必要再算反着的了，直接用总和减即可

这一点和前面三种方法都可以组合，形成六种方法。

然而我最推荐的是这第七种方法，求和列表法，也要结合上面的那一个信息。

我们设一个列表，[d0,d1,d2,d3,d4,…,]每一个dx代表从起始站到第x号车站的距离。那么第一项就是d0 = 0,最后一项是绕成一个环以后又回到起点的距离。

那么我们求x到y的距离，实际上就是求0到y的距离减去0到x的距离，与总环长度减去（0到y的距离减去0到x的距离），即min(_sum[b] - _sum[a], _sum[-1] - _sum[b] + _sum[a])

这种方法是复杂度最低的。

参考

https://qsctech-sange.github.io/1046-Shortest-Distance

一元多项式求导

设计函数求一元多项式的导数。（注：xn（n为整数）的一阶导数为n*xn-1。）

输入格式：

以指数递降方式输入多项式非零项系数和指数（绝对值均为不超过1000的整数）。数字间以空格分隔。

输出格式：

以与输入相同的格式输出导数多项式非零项的系数和指数。数字间以空格分隔，但结尾不能有多余空格。注意“零多项式”的指数和系数都是0，但是表示为“0 0”。

输入样例：

3 4 -5 2 6 1 -2 0

输出样例：

12 3 -10 1 6 0

A+B for Polynomials

题目：计算多项式A+B的和～

Sample Input

2 1 2.4 0 3.2

2 2 1.5 1 0.5

Sample Output

3 2 1.5 1 2.9 0 3.2

分析：设立c数组，长度为指数的最大值，c[i] = j表示指数i的系数为j，接收a和b输入的同时将对应指数的系数加入到c中，累计c中所有非零系数的个数，然后从后往前输出所有系数不为0的指数和系数～

Product of Polynomials

题目：给出两个多项式A和B，求A*B的结果～

Sample Input

2 1 2.4 0 3.2

2 2 1.5 1 0.5

Sample Output

3 3 3.6 2 6.0 1 1.6

分析：double类型的arr数组保存第一组数据，ans数组保存结果。当输入第二组数据的时候，一边进行运算一边保存结果。最后按照指数递减的顺序输出所有不为0的项～

注意：因为相乘后指数可能最大为2000，所以ans数组最大要开到2001

本文标题：《简单模拟》

本文链接：https://wnag.com.cn/933.html

特别声明：除特别标注，本站文章均为原创，本站文章原则上禁止转载，如确实要转载，请电联：[email protected]，尊重他人劳动成果，谢过~