簡單模拟

例題一覽（可看着這些題目想出來代碼才算過關）

（全程注意封裝，養成良好的面向對象思維）

• 害死人不償命的（3n+1）猜想（卡拉茲幻想）
• 挖掘機技術哪家強
• A+B和C
• A+B and C（64Bit）
• 部分A+B
• 程式運作時間
• 劃拳
• 數組元素循環右移問題
• 數字分類
• 錘子剪子布
• Shuffling Machine
• Shortest Distance
• 一進制多項式求導
• A+B for Polynomials
• Product of Polynomials

害死人不償命的（3n+1）猜想（卡拉茲幻想）

輸入一個數，偶數時則砍掉一半；奇數時，則（3n+1）砍掉一半，最後直到得到1.

問，進行了多少次？

挖掘機技術哪家強

題目描述

為了用事實說明挖據機技術到底哪家強,PAT組織了一場挖據機技能大賽。請根據比賽結果統計出技術最強的那個學校。

輸入格式

在第1行給出不超過10的正整數N,即參賽人數。随後N行,每行給出一位參賽者的資訊和成績,包括其所代表的學校的編号(從1開始連續編号)及其比賽成績(百分制),中間以空格分隔。

輸出格式

在一行中給出總得分最高的學校的編号及其總分,中間以空格分隔。題目保證答案唯一,沒有并列。

輸入樣例

6

3 65

2 80

1 100

2 70

3 40

3 0

輸出樣例

2 150

A+B和C

題目描述

給定區間 [−2^31,2^31] 内的 3 個整數 A、B 和 C，請判斷 A+B 是否大于 C。

輸入格式：

輸入第 1 行給出正整數 T (≤10)，是測試用例的個數。随後給出 T 組測試用例，每組占一行，順序給出 A、B和 C。整數間以空格分隔。

輸出格式：

對每組測試用例，在一行中輸出 Case #X: true 如果 A+B>C，否則輸出 Case #X: false，其中 X 是測試用例的編号（從 1 開始）。

4

1 2 3

2 3 4

2147483647 0 2147483646

0 -2147483648 -2147483647

A+B and C（64Bit）

給定 [− 2^63,2^63]中的三個整數A，B和C，您應該确定是否A + B> C。

輸入規格：

輸入的第一行給出測試用例的正數T（≤10）。然後是T個測試用例，每個用例包含一行，其中包含三個整數A，B和C，以單個空格分隔。

輸出規格：

對于每個測試用例，在一行中輸出情況#X：如果A + B> C，則為true

A + B> C或KaTeX解析錯誤：預期為'EOF'，在位置6獲得'＃'：案例＃̲X：否則為false，其中X為案例編号（從1開始）。

Sample Input:

3

1 2 3

2 3 4

9223372036854775807 -9223372036854775808 0           

複制

Sample Output:

Case #1: false

    Case #2: true

    Case #3: false           

複制

部分A+B

正整數A的“DA（為1位整數）部分”定義為由A中所有DA組成的新整數PA。例如：給定A = 3862767，DA = 6，則A的“6部分”PA是66，因為A中有2個6。

現給定A、DA、B、DB，請編寫程式計算PA + PB。

輸入格式：

輸入在一行中依次給出A、DA、B、DB，中間以空格分隔，其中0 < A, B < 10^10。

輸出格式：

在一行中輸出PA + PB的值。

輸入樣例1：

3862767 6 13530293 3

輸出樣例1：

399

程式運作時間

要獲得一個C語言程式的運作時間，常用的方法是調用頭檔案time.h，其中提供了clock()函數，可以捕捉從程式開始運作到clock()被調用時所耗費的時間。這個時間機關是clock tick，即“時鐘打點”。同時還有一個常數CLK_TCK，給出了機器時鐘每秒所走的時鐘打點數。于是為了獲得一個函數f的運作時間，我們隻要在調用f之前先調用clock()，獲得一個時鐘打點數C1；在f執行完成後再調用clock()，獲得另一個時鐘打點數C2；兩次獲得的時鐘打點數之差(C2-C1)就是f運作所消耗的時鐘打點數，再除以常數CLK_TCK，就得到了以秒為機關的運作時間。這裡不妨簡單假設常數CLK_TCK為100。現給定被測函數前後兩次獲得的時鐘打點數，請你給出被測函數運作的時間。

輸入格式：

輸入在一行中順序給出2個整數C1和C1。注意兩次獲得的時鐘打點數肯定不相同，即C1 < C2，并且取值在[0, 10^7]。

輸出格式：

在一行中輸出被測函數運作的時間。運作時間必須按照“hh:mm:ss”（即2位的“時:分:秒”）

格式輸出；不足1秒的時間四舍五入到秒。

輸入樣例：

123 4577973

輸出樣例：

12:42:59

劃拳

劃拳是古老中國酒文化的一個有趣的組成部分。酒桌上兩人劃拳的方法為：每人口中喊出一個數字，同時用手比劃出一個數字。如果誰比劃出的數字正好等于兩人喊出的數字之和，誰就赢了，輸家罰一杯酒。兩人同赢或兩人同輸則繼續下一輪，直到唯一的赢家出現。

下面給出甲、乙兩人的劃拳記錄，請你統計他們最後分别喝了多少杯酒。

輸入格式：

輸入第一行先給出一個正整數N（<=100），随後N行，每行給出一輪劃拳的記錄，格式為：

甲喊 甲劃 乙喊 乙劃

其中“喊”是喊出的數字，“劃”是劃出的數字，均為不超過100的正整數（兩隻手一起劃）。

輸出格式：

在一行中先後輸出甲、乙兩人喝酒的杯數，其間以一個空格分隔。

數組元素循環右移問題

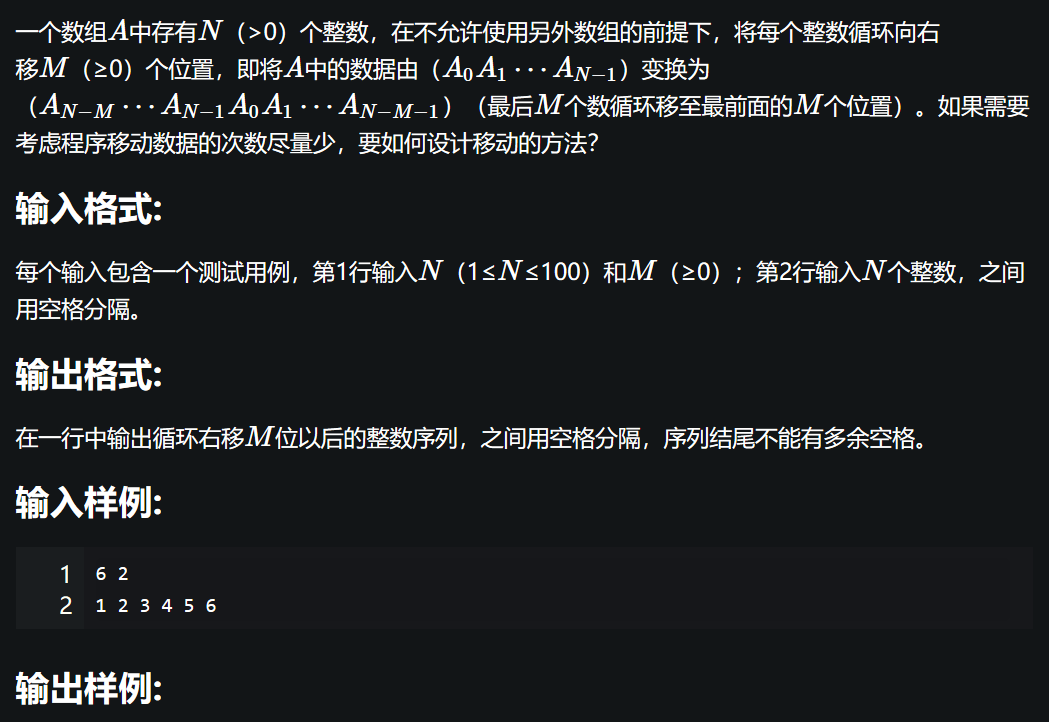
數字分類

給定一系列正整數，請按要求對數字進行分類，并輸出以下5個數字：

A1 = 能被5整除的數字中所有偶數的和；

A2 = 将被5除後餘1的數字按給出順序進行交錯求和，即計算n1-n2+n3-n4...；

A3 = 被5除後餘2的數字的個數；

A4 = 被5除後餘3的數字的平均數，精确到小數點後1位；

A5 = 被5除後餘4的數字中最大數字。

輸入格式：

每個輸入包含1個測試用例。每個測試用例先給出一個不超過1000的正整數N，随後給出N個不超過1000的待分類的正整數。數字間以空格分隔。

輸出格式：

對給定的N個正整數，按題目要求計算A1~A5并在一行中順序輸出。數字間以空格分隔，但行末不得有多餘空格。

若其中某一類數字不存在，則在相應位置輸出“N”。

輸入樣例1：

13 1 2 3 4 5 6 7 8 9 10 20 16 18

輸出樣例1：

30 11 2 9.7 9

輸入樣例2：

8 1 2 4 5 6 7 9 16

輸出樣例2：

N 11 2 N 9

錘子剪子布

大家應該都會玩“錘子剪刀布”的遊戲：兩人同時給出手勢，勝負規則如圖所示：現給出兩人的交鋒記錄，請統計雙方的勝、平、負次數，并且給出雙方分别出什麼手勢的勝算最大。

輸入格式：

輸入第1行給出正整數N（<=105），即雙方交鋒的次數。随後N行，每行給出一次交鋒的資訊，即甲、乙雙方同時給出的的手勢。C代表“錘子”、J代表“剪刀”、B代表“布”，第1個字母代表甲方，第2個代表乙方，中間有1個空格。

輸出格式：

輸出第1、2行分别給出甲、乙的勝、平、負次數，數字間以1個空格分隔。第3行給出兩個字母，分别代表甲、乙獲勝次數最多的手勢，中間有1個空格。如果解不唯一，則輸出按字母序最小的解。

輸入樣例：

10

C J

J B

C B

B B

B C

C C

C B

J B

B C

J J

輸出樣例：

5 3 2

2 3 5

B B

Shuffling Machine

Shortest Distance

(挖坑，待解決)

題目的意思是，有一些環形站點，給你這幾個站點和鄰居之間的距離，然後給你兩個站點編号，求它們的最近距離。

很多種方法

第一種是順着思路，正着搜一遍，反着搜一遍。遇到清單尾巴了就移到0,相當于環形了。優點是直覺友善。

第二種是，直接把原來的距離數組複制一遍，然後就搜兩次，一次從原來的begin和end搜，一次搜end到distance + begin 的距離。優點是代碼少。缺點是空間複雜度高且算法沒什麼本質上的卵用。

還有一種是動态規劃法。

既然題目已經提示有多次查詢，那麼把以前的計算記錄存儲起來就很自然。

方法是，開一個二維數組dp，對于dp[i][j]的含義就是，從i車站沿車站号增大的方向到車站j所需要的路程。比如dp[2][3]表示從車站2開到車站3的路程，而dp[3][2]就是從車站3開到最後一個車站繞回第0車站再開到車站2的路程。

我們初始化dp數組都是0

然後讀入資料

周遊車站号，從0到總車站

這個車站到下一個車站的距離就是讀入的資料。下一個車站用(i+1)% len(stations) 這樣的取餘的方式，可以規避最後加一要回到原點的問題。

接下來按照距離周遊，因為自己和自己的距離是0,自己和下一個車站的距離已經給出，是以距離從2周遊到車站數量-1

每次車站i到車站j的距離就相當于車站i到車站j-1加上車站j-1到車站j的距離。這是狀态轉移公式。因為是按照距離從小到大計算的，是以等号右邊的一定是已經計算過的。同時用老方法規避回到起點的問題。寫成代碼就是

dp[j][(j + i) % len(dis)] = dp[j][(j + i - 1) % len(dis)] + dp[(j + i - 1) % len(dis)][(j + i) % len(dis)]

其中，i是周遊的距離

輸出的時候取dp[i][j]與dp[j][i]的較小值即可。

以上三種方法都沒有利用到一個資訊。

就是整個環的長度都是固定的，假設為S，那麼正着走距離是A，反着走距離一定是S-A

是以算完正的就沒必要再算反着的了，直接用總和減即可

這一點和前面三種方法都可以組合，形成六種方法。

然而我最推薦的是這第七種方法，求和清單法，也要結合上面的那一個資訊。

我們設一個清單，[d0,d1,d2,d3,d4,…,]每一個dx代表從起始站到第x号車站的距離。那麼第一項就是d0 = 0,最後一項是繞成一個環以後又回到起點的距離。

那麼我們求x到y的距離，實際上就是求0到y的距離減去0到x的距離，與總環長度減去（0到y的距離減去0到x的距離），即min(_sum[b] - _sum[a], _sum[-1] - _sum[b] + _sum[a])

這種方法是複雜度最低的。

參考

https://qsctech-sange.github.io/1046-Shortest-Distance

一進制多項式求導

設計函數求一進制多項式的導數。（注：xn（n為整數）的一階導數為n*xn-1。）

輸入格式：

以指數遞降方式輸入多項式非零項系數和指數（絕對值均為不超過1000的整數）。數字間以空格分隔。

輸出格式：

以與輸入相同的格式輸出導數多項式非零項的系數和指數。數字間以空格分隔，但結尾不能有多餘空格。注意“零多項式”的指數和系數都是0，但是表示為“0 0”。

輸入樣例：

3 4 -5 2 6 1 -2 0

輸出樣例：

12 3 -10 1 6 0

A+B for Polynomials

題目：計算多項式A+B的和～

Sample Input

2 1 2.4 0 3.2

2 2 1.5 1 0.5

Sample Output

3 2 1.5 1 2.9 0 3.2

分析：設立c數組，長度為指數的最大值，c[i] = j表示指數i的系數為j，接收a和b輸入的同時将對應指數的系數加入到c中，累計c中所有非零系數的個數，然後從後往前輸出所有系數不為0的指數和系數～

Product of Polynomials

題目：給出兩個多項式A和B，求A*B的結果～

Sample Input

2 1 2.4 0 3.2

2 2 1.5 1 0.5

Sample Output

3 3 3.6 2 6.0 1 1.6

分析：double類型的arr數組儲存第一組資料，ans數組儲存結果。當輸入第二組資料的時候，一邊進行運算一邊儲存結果。最後按照指數遞減的順序輸出所有不為0的項～

注意：因為相乘後指數可能最大為2000，是以ans數組最大要開到2001

版權所有：可定部落格 © WNAG.COM.CN

本文标題：《簡單模拟》

本文連結：https://wnag.com.cn/933.html

特别聲明：除特别标注，本站文章均為原創，本站文章原則上禁止轉載，如确實要轉載，請電聯：[email protected]，尊重他人勞動成果，謝過~