luogu1983[NOIP2013pjT4] 车站分级(拓扑排序)

题目描述

一条单向的铁路线上，依次有编号为 1, 2, …, n 的 n 个火车站。每个火车站都有一个级别，最低为 1 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 x，则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

例如，下表是 5 趟车次的运行情况。其中，前 4 趟车次均满足要求，而第 5 趟车次由于停靠了 3 号火车站（2 级）却未停靠途经的 6 号火车站（亦为 2 级）而不满足要求。

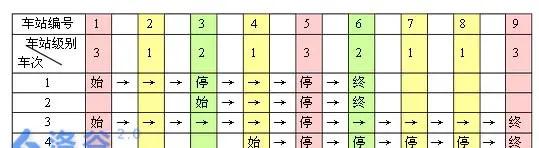
现有 m 趟车次的运行情况（全部满足要求），试推算这 n 个火车站至少分为几个不同的级别。

输入输出格式

输入格式：

输入文件为 level.in。

第一行包含 2 个正整数 n, m，用一个空格隔开。

第 i + 1 行（1 ≤ i ≤ m）中，首先是一个正整数 si（2 ≤ si ≤ n），表示第 i 趟车次有 si 个停靠站；接下来有 si个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式：

输出文件为 level.out。

输出只有一行，包含一个正整数，即 n 个火车站最少划分的级别数。

输入输出样例

输入样例#1： 复制

9 2 
4 1 3 5 6 
3 3 5 6      

输出样例#1： 复制

2      

输入样例#2： 复制

9 3 
4 1 3 5 6 
3 3 5 6 
3 1 5 9      

输出样例#2： 复制

3      

说明

对于 20%的数据，1 ≤ n, m ≤ 10；

对于 50%的数据，1 ≤ n, m ≤ 100；

对于 100%的数据，1 ≤ n, m ≤ 1000。

1 #include "bits/stdc++.h"
 2 using namespace std;
 3 typedef long long LL;
 4 const int MAX1=1005,MAX2=MAX1*MAX1;
 5 int n,m,ans,du[MAX1],a[MAX1],deep[MAX1],f[MAX1][MAX1];
 6 int tot,head[MAX1],adj[MAX2<<1],next[MAX2<<1];
 7 inline int read(){
 8     int an=0,x=1;char c=getchar();
 9     while (c<'0' || c>'9') {if (c=='-') x=-1;c=getchar();}
10     while (c>='0' && c<='9') {an=(an<<3)+(an<<1)+c-'0';c=getchar();}
11     return an*x;
12 }
13 void addedge(int u,int v){
14     tot++,du[v]++;f[u][v]=1,adj[tot]=v,next[tot]=head[u],head[u]=tot;
15 }
16 void topsort(){
17     int i,j;
18     queue <int> q;
19     for (i=1;i<=n;i++) if (!du[i]) deep[i]=1,q.push(i);
20     while (!q.empty()){
21         int u=q.front();q.pop();
22         for (i=head[u];i;i=next[i]){
23             deep[adj[i]]=max(deep[adj[i]],deep[u]+1);
24             du[adj[i]]--;
25             if (!du[adj[i]]) q.push(adj[i]);
26         }
27     }
28 }
29 int main(){
30     freopen ("level.in","r",stdin);freopen ("level.out","w",stdout);
31     int i,j,k;bool vis[MAX1];
32     n=read(),m=read();
33     for (i=1;i<=m;i++){
34         a[0]=read();
35         memset(vis,false,sizeof(vis));
36         for (j=1;j<=a[0];j++) a[j]=read(),vis[a[j]]=true;
37         for (j=1;j<=a[0];j++)
38             for (k=a[1]+1;k<a[a[0]];k++)
39                 if (!vis[k] && !f[a[j]][k])
40                     addedge(a[j],k);
41     }
42     topsort();
43     for (i=1;i<=n;i++) ans=max(ans,deep[i]);
44     printf("%d",ans);
45     return 0;
46