《编程之美: 求二叉树中节点的最大距离》的另一个解法

http://www.cnblogs.com/miloyip/archive/2010/02/25/1673114.html

问题定义

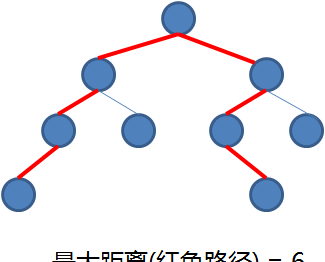
如果我们把二叉树看成一个图，父子节点之间的连线看成是双向的，我们姑且定义"距离"为两节点之间边的个数。写一个程序求一棵二叉树中相距最远的两个节点之间的距离。

书上的解法

书中对这个问题的分析是很清楚的，我尝试用自己的方式简短覆述。

计算一个二叉树的最大距离有两个情况:

• 情况A: 路径经过左子树的最深节点，通过根节点，再到右子树的最深节点。
• 情况B: 路径不穿过根节点，而是左子树或右子树的最大距离路径，取其大者。

只需要计算这两个情况的路径距离，并取其大者，就是该二叉树的最大距离。

我也想不到更好的分析方法。

但接着，原文的实现就不如上面的清楚 (源码可从这里下载):

01

// 数据结构定义

02	struct NODE

03

{

04	NODE* pLeft;         // 左子树

05	NODE* pRight;        // 右子树

06	int nMaxLeft;        // 左子树中的最长距离

07	int nMaxRight;       // 右子树中的最长距离

08	char chValue;        // 该节点的值

09

};

10

11	int nMaxLen = 0;

12

13	// 寻找树中最长的两段距离

14	void FindMaxLen(NODE* pRoot)

15

{

16	// 遍历到叶子节点，返回

17	if (pRoot == NULL)

18

{

19

return ;

20

}

21

22	// 如果左子树为空，那么该节点的左边最长距离为0

23	if (pRoot -> pLeft == NULL)

24

{

25	pRoot -> nMaxLeft = 0;

26

}

27

28	// 如果右子树为空，那么该节点的右边最长距离为0

29	if (pRoot -> pRight == NULL)

30

{

31	pRoot -> nMaxRight = 0;

32

}

33

34	// 如果左子树不为空，递归寻找左子树最长距离

35	if (pRoot -> pLeft != NULL)

36

{

37	FindMaxLen(pRoot -> pLeft);

38

}

39

40	// 如果右子树不为空，递归寻找右子树最长距离

41	if (pRoot -> pRight != NULL)

42

{

43	FindMaxLen(pRoot -> pRight);

44

}

45

46	// 计算左子树最长节点距离

47	if (pRoot -> pLeft != NULL)

48

{

49	int nTempMax = 0;

50	if (pRoot -> pLeft -> nMaxLeft > pRoot -> pLeft -> nMaxRight)

51

{

52	nTempMax = pRoot -> pLeft -> nMaxLeft;

53

}

54

else

55

{

56	nTempMax = pRoot -> pLeft -> nMaxRight;

57

}

58	pRoot -> nMaxLeft = nTempMax + 1;

59

}

60

61	// 计算右子树最长节点距离

62	if (pRoot -> pRight != NULL)

63

{

64	int nTempMax = 0;

65	if (pRoot -> pRight -> nMaxLeft > pRoot -> pRight -> nMaxRight)

66

{

67	nTempMax = pRoot -> pRight -> nMaxLeft;

68

}

69

else

70

{

71	nTempMax = pRoot -> pRight -> nMaxRight;

72

}

73	pRoot -> nMaxRight = nTempMax + 1;

74

}

75

76

// 更新最长距离

77	if (pRoot -> nMaxLeft + pRoot -> nMaxRight > nMaxLen)

78

{

79	nMaxLen = pRoot -> nMaxLeft + pRoot -> nMaxRight;

80

}

81

}

这段代码有几个缺点:

1. 算法加入了侵入式(intrusive)的资料nMaxLeft, nMaxRight
2. 使用了全局变量 nMaxLen。每次使用要额外初始化。而且就算是不同的独立资料，也不能在多个线程使用这个函数
3. 逻辑比较复杂，也有许多 NULL 相关的条件测试。

我的尝试

我认为这个问题的核心是，情况A 及 B 需要不同的信息: A 需要子树的最大深度，B 需要子树的最大距离。只要函数能在一个节点同时计算及传回这两个信息，代码就可以很简单:

01	#include <iostream>

02

03	using namespace std;

04

05	struct NODE

06

{

07	NODE *pLeft;

08	NODE *pRight;

09

};

10

11	struct RESULT

12

{

13	int nMaxDistance;

14	int nMaxDepth;

15

};

16

17	RESULT GetMaximumDistance(NODE* root)

18

{

19	if (!root)

20

{

21	RESULT empty = { 0, -1 };    // trick: nMaxDepth is -1 and then caller will plus 1 to balance it as zero.

22	return empty;

23

}

24

25	RESULT lhs = GetMaximumDistance(root->pLeft);

26	RESULT rhs = GetMaximumDistance(root->pRight);

27

28	RESULT result;

29	result.nMaxDepth = max(lhs.nMaxDepth + 1, rhs.nMaxDepth + 1);

30	result.nMaxDistance = max(max(lhs.nMaxDistance, rhs.nMaxDistance), lhs.nMaxDepth + rhs.nMaxDepth + 2);

31	return result;

32

}

计算 result 的代码很清楚；nMaxDepth 就是左子树和右子树的深度加1；nMaxDistance 则取 A 和 B 情况的最大值。

为了减少 NULL 的条件测试，进入函数时，如果节点为 NULL，会传回一个 empty 变量。比较奇怪的是 empty.nMaxDepth = -1，目的是让调用方 +1 后，把当前的不存在的 (NULL) 子树当成最大深度为 0。

除了提高了可读性，这个解法的另一个优点是减少了 O(节点数目) 大小的侵入式资料，而改为使用 O(树的最大深度) 大小的栈空间。这个设计使函数完全没有副作用(side effect)。

测试代码

以下也提供测试代码给读者参考 (页数是根据第7次印刷，节点是由上至下、左至右编号):

view source print ?

01	void Link(NODE* nodes,  int parent,  int left,  int right)

02

{

03	if (left != -1)

04	nodes[parent].pLeft = &nodes[left];

05

06	if (right != -1)

07	nodes[parent].pRight = &nodes[right];

08

}

09

10	void main()

11

{

12	// P. 241 Graph 3-12

13	NODE test1[9] = { 0 };

14	Link(test1, 0, 1, 2);

15	Link(test1, 1, 3, 4);

16	Link(test1, 2, 5, 6);

17	Link(test1, 3, 7, -1);

18	Link(test1, 5, -1, 8);

19	cout <<  "test1: " << GetMaximumDistance(&test1[0]).nMaxDistance << endl;

20

21	// P. 242 Graph 3-13 left

22	NODE test2[4] = { 0 };

23	Link(test2, 0, 1, 2);

24	Link(test2, 1, 3, -1);

25	cout <<  "test2: " << GetMaximumDistance(&test2[0]).nMaxDistance << endl;

26

27	// P. 242 Graph 3-13 right

28	NODE test3[9] = { 0 };

29	Link(test3, 0, -1, 1);

30	Link(test3, 1, 2, 3);

31	Link(test3, 2, 4, -1);

32	Link(test3, 3, 5, 6);

33	Link(test3, 4, 7, -1);

34	Link(test3, 5, -1, 8);

35	cout <<  "test3: " << GetMaximumDistance(&test3[0]).nMaxDistance << endl;

36

37	// P. 242 Graph 3-14

38	// Same as Graph 3-2, not test

39

40	// P. 243 Graph 3-15

41	NODE test4[9] = { 0 };

42	Link(test4, 0, 1, 2);

43	Link(test4, 1, 3, 4);

44	Link(test4, 3, 5, 6);

45	Link(test4, 5, 7, -1);

46	Link(test4, 6, -1, 8);

47	cout <<  "test4: " << GetMaximumDistance(&test4[0]).nMaxDistance << endl;

48

}

你想到更好的解法吗?