1. 数据结构三要素
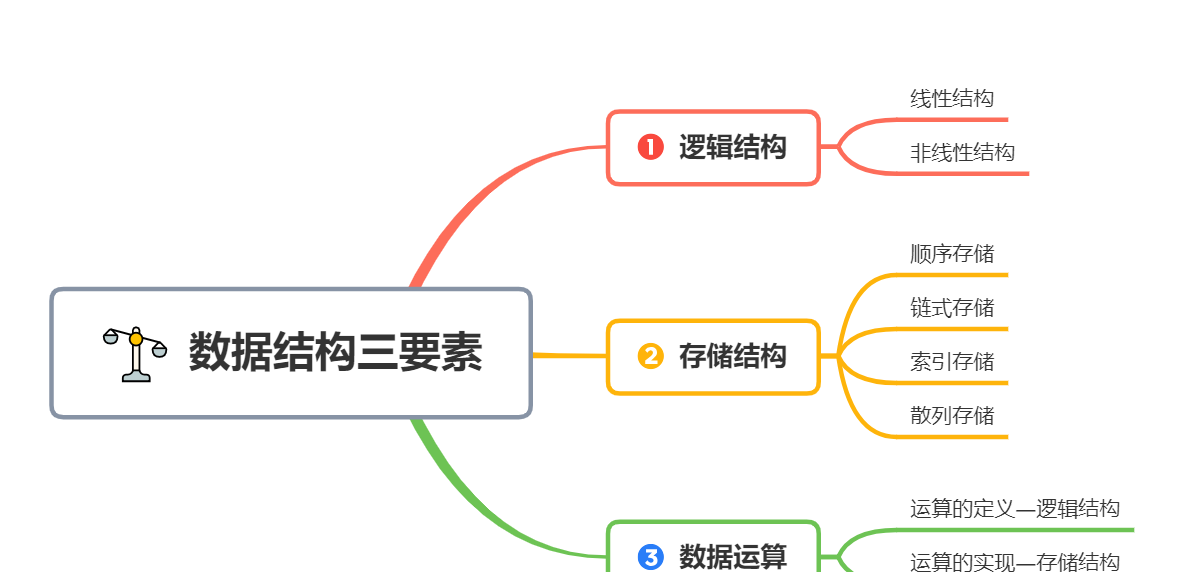
1)逻辑结构 指的是数据间的逻辑关系,与数据的存储无关,独立于计算机之外。它又分为线性结构和非线性结构
- 线性结构:线性表,栈,队列,串,数组和广义表
- 非线性结构:树,图,集合
2)存储结构 是逻辑结构的存储映像,就是数据间的关系在计算机中的表现形式。也成为物理结构。它又分为 4 类:顺序存储 ,链式存储,索引存储和散列存储
- 顺序存储:把逻辑上相邻的元素存储在物理位置也相邻的存储单元里
- 链式存储:不要求物理位置的相邻,借助指示元素存储地址的指针表示元素之间的逻辑关系
- 索引存储:在存储元素信息的同时,添加附加的索引表,通过索引对节点进行操作
- 散列存储:也称 Hash 存储,根据结点的关键字通过散列函数计算出结点的存储地址
相同的逻辑结构在计算机里可以用不同的存储结构实现。比如逻辑结构中的线性结构,可以用数组(顺序存储)或单向链表(链接存储)来实现。
3)数据运算: 施加在数据上的运算(包括定义与实现)。运算的定义是针对逻辑结构,运算的实现是针对物理结构
2. 线性表的定义
线性表定义:
- 具有相同数据类型的 n 个数据元素的有限序列
- 线性表是一种逻辑结构,表示元素之间一对一的逻辑关系
使用线性表存储数据的方式可以这样理解,把所有数据用一根线儿串起来,再存储到物理空间中
下图中,左侧是“串”起来的数据,右侧是空闲的物理空间。把这 “一串儿” 数据放置到物理空间,我们可以选择以下两种方式:
将具有“一对一”关系的数据“线性”地存储到物理空间中,这种存储结构就称为线性存储结构:
- ① 顺序表(如上图左边):将数据依次存储在连续的整块物理空间中
- ② 链表(如上图右边):数据分散的存储在物理空间中,通过一根线保存着它们之间的逻辑关系
- 单链表
- 双链表
- 循环单链表
- 循环双链表
下面详细讲解这两种存储结构 ????
3. 顺序表
① 顺序表定义
线性表的顺序存储。逻辑上相邻的两个元素在物理位置上也相邻
数组就是顺序表,下标一般从 0 开始:
顺序表的特点:
- 随机访问(通过首地址和元素序号可在时间 O(1) 内找到元素)
- 插入和删除需要移动大量元素
- 存储密度高,每个结点只存储数据元素
② 顺序表基本操作
Ⅰ 插入
在数组 a 的第 i 个位置 (下标 i-1) 插入元素 e
// 第i个元素及其之后的元素后移for (int j = a.length; j >= i; j--)
a[j] = a[j - 1];
a[i - 1] = e;
length++;复制代码 - 最好情况:在表尾插入,时间复杂度 O(1)
- 最坏情况:在表头插入,时间复杂度 O(n)
- 平均情况:时间复杂度 O(n)
Ⅱ 删除
删除数组 a 的第 i 个位置的元素
// 从第 i 个位置元素前移for(int j = i; j < a.length; j++)
a[j-1] = a[j];
length --;复制代码 - 最好情况:删除表尾元素,时间复杂度 O(1)
- 最坏情况:删除表头元素,时间复杂度 O(n)
Ⅲ 按值查找
查找数组 a 中值为 e 的元素的下标
for (int i = 0; i < a.length; i++)if (a[i] == e)return i;复制代码 - 最好情况:查找元素在表头,时间复杂度 O(1)
- 最坏情况:查找元素在表尾,时间复杂度 O(n)
4. 链表
① 链表的定义与结构
线性表的链式存储。逻辑上相邻的两个元素在物理位置不一定也相邻
例如,使用链表存储 {1,2,3},数据的物理存储状态如下图所示:
可以看到,上图根本无法体现出各数据之间的逻辑关系。对此,链表的解决方案是,每个数据元素在存储时都配备一个指针,用于指向自己的直接后继元素。如下图所示:
当然,指针可以指向自己的直接后继元素,也可以指向自己的直接前驱元素。为此,链表可分为:
- 单链表(指针指向自己的直接后继元素)
- 双链表(指针指向自己的直接后继元素和直接前驱元素)
- 循环单链表(指针指向自己的直接后继元素,表尾节点的指针指向头节点)
- 循环双链表(指针指向自己的直接后继元素和直接前驱元素,表尾节点的指针指向头节点)
通过以上大家应该也知道了,链表中每个数据的存储都由以下两部分组成:
- 数据域:数据元素本身
- 指针域:指向该元素直接后继/前驱/...元素的指针
上图所示的结构在链表中称为节点。也就是说,链表实际存储的是一个一个的节点,真正的数据元素包含在这些节点中,举个单链表的例子:
???? 当然,上所示的链表结构并不完整。一个完整的链表需要由以下几部分构成:
- 头指针:一个普通的指针,它的特点是永远指向链表第一个节点的位置。很明显,头指针用于指明链表的位置,便于后期找到链表并使用表中的数据
- 节点:链表中的节点又分为头节点、首元节点和其他节点
- 头节点:其实就是一个不存任何数据的空节点,通常作为链表的第一个节点。对于链表来说,头节点不是必须的,它的作用只是为了方便解决某些实际问题
- 首元节点:由于头节点(也就是空节点)的缘故,链表中称第一个存有数据的节点为首元节点。首元节点只是对链表中第一个存有数据节点的一个称谓,用于和头节点进行区分,没有实际意义
- 其他节点:链表中其他的节点
因此,一个存储 {1,2,3} 的完整单链表结构如图所示:
???? 引入头节点的优点:
- 链表的首元节点的操作与其他位置的元素操作一样,无须进行特殊处理
- 无论链表是否为空,其头指针都是指向头节点的非空指针,空表和非空表的处理得到了统一
② 单链表
Ⅰ 定义
单链表就是指针指向自己的直接后继元素的链表
以 Java 为例,我们自定义一个单链表结构:
public class Node{private T t;private Node next;
......
}复制代码 单链表可以解决顺序表需要大量连续存储空间的缺点,但单链表附加指针域,也存在浪费存储空间的缺点
单链表是非随机存储的存储结构:即不能直接找到表中某个特点的结点。需要从头开始遍历。
单链表访问前驱的时间复杂度为 O(n),访问后继 O(1)
Ⅱ 基本操作
头插法
在头节点 L 的后面插入节点 s,即 s 节点成为当前链表的首元节点
头插法的读入顺序和生成顺序相反
s.next = L.next;
L.next = s;复制代码 尾插法
在链表最后一个节点 r 的后面插入节点 s,即 s 节点成为当前链表的最后一个节点
尾插法的读入顺序和生成顺序相同
r.next = s;
r = s; // s 节点成为链表的最后一个节点复制代码 插入节点
p 节点之后插入 s 节点
s.next = p.next;
p.next = s;复制代码 删除节点
p 节点之后删除 q 节点
// 删除 p 之后的 q q = p.next;
p.next = q.next;复制代码 ③ 双链表
双链表就是同时具有前驱指针和后继指针的链表
双链表访问前驱和后继结点时间复杂度都是 O(1)
以 Java 为例,我们自定义一个双链表结构:
public class Node{private T t;private Node next;private Node prior;
......
}复制代码 上图中 2、3 顺序可调换
s.next = p.next;
p.next.prior = s;
p.next = s;
s.prior = p;复制代码 删除 p 节点之后的 s 节点
p.next = s.next;
s.next.prior = p;复制代码 ③ 循环单链表
循环单链表就是表尾节点的指针指向头节点的单链表
判空条件:表尾结点的 next 是否是等于头指针
④ 循环双链表
循环双链表就是表尾节点的指针指向头节点的双链表
5. 顺序表和链表的比较
1)存取方式
- 顺序表可以顺序存取,也可以随机存取
- 链表只能从表头顺序存取元素
2)逻辑结构与物理结构
- 顺序存储时,逻辑上相邻的元素,对应的物理存储位置也相邻
- 链式存储时,逻辑上相邻的元素,物理存储位置不一定相邻,其逻辑关系是通过指针链接来表示的
3)查找、插入和删除操作
-
对于按值查找,顺序表无序时,两者的时间复杂度均为 O(n);顺序表有序时,可采用折半查找,此时的时间复杂度为 O(log2n)
对于按序号查找,顺序表支持随机访问,时间复杂度仅为 O(1),而链表的平均时间复杂度为 O(n)。
-
顺序表的插入、删除操作,平均需要移动半个表长的元素
链表的插入、删除操作,只需要修改相关结点的指针域既可。由于链表的每个结点都有指针域,所以在存储空间上要比顺序表付出的代价大,存储密度不够大。
4)空间分配
-
顺序存储在静态存储分配情况下,一旦存储空间装满就不能扩充,若再加入新元素,则会出现溢出,所以需要预先分配足够大的存储空间。预先分配过大,可能会导致顺序表候补大量闲置;预先分配过小,又会造成溢出。
动态存储分配虽然存储空间可以扩充,但需要移动大量元素,导致操作效率降低,而且若内存中没有更大的连续存储空间,则会导致分配失败