1. 資料結構三要素
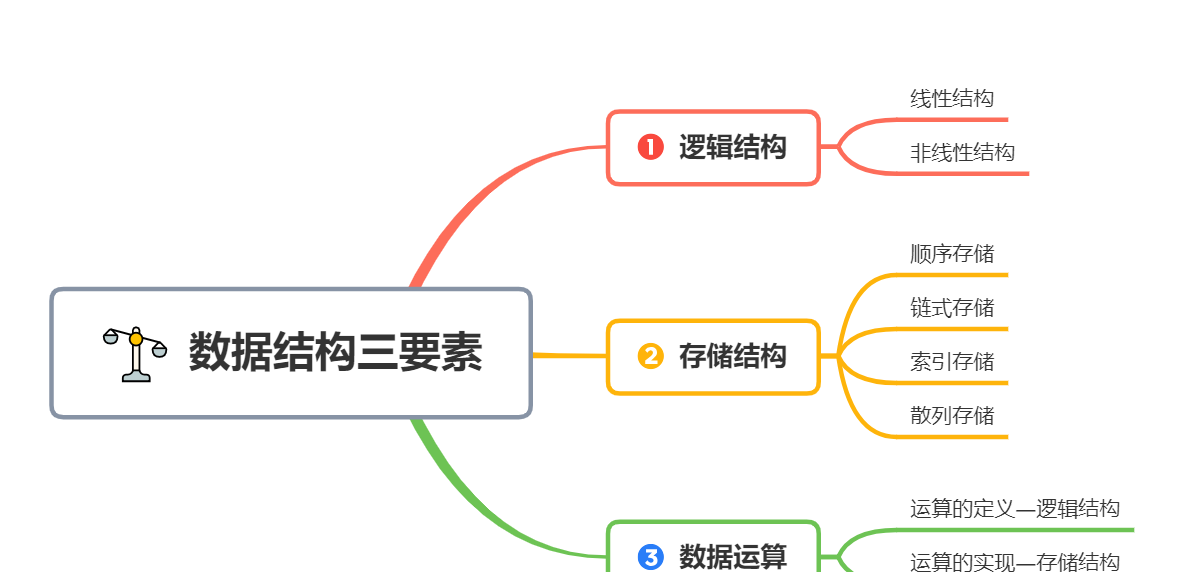
1)邏輯結構 指的是資料間的邏輯關系,與資料的存儲無關,獨立于計算機之外。它又分為線性結構和非線性結構
- 線性結構:線性表,棧,隊列,串,數組和廣義表
- 非線性結構:樹,圖,集合
2)存儲結構 是邏輯結構的存儲映像,就是資料間的關系在計算機中的表現形式。也成為實體結構。它又分為 4 類:順序存儲 ,鍊式存儲,索引存儲和散列存儲
- 順序存儲:把邏輯上相鄰的元素存儲在實體位置也相鄰的存儲單元裡
- 鍊式存儲:不要求實體位置的相鄰,借助訓示元素存儲位址的指針表示元素之間的邏輯關系
- 索引存儲:在存儲元素資訊的同時,添加附加的索引表,通過索引對節點進行操作
- 散列存儲:也稱 Hash 存儲,根據結點的關鍵字通過散列函數計算出結點的存儲位址
相同的邏輯結構在計算機裡可以用不同的存儲結構實作。比如邏輯結構中的線性結構,可以用數組(順序存儲)或單向連結清單(連結存儲)來實作。
3)資料運算: 施加在資料上的運算(包括定義與實作)。運算的定義是針對邏輯結構,運算的實作是針對實體結構
2. 線性表的定義
線性表定義:
- 具有相同資料類型的 n 個資料元素的有限序列
- 線性表是一種邏輯結構,表示元素之間一對一的邏輯關系
使用線性表存儲資料的方式可以這樣了解,把所有資料用一根線兒串起來,再存儲到實體空間中
下圖中,左側是“串”起來的資料,右側是空閑的實體空間。把這 “一串兒” 資料放置到實體空間,我們可以選擇以下兩種方式:
将具有“一對一”關系的資料“線性”地存儲到實體空間中,這種存儲結構就稱為線性存儲結構:
- ① 順序表(如上圖左邊):将資料依次存儲在連續的整塊實體空間中
- ② 連結清單(如上圖右邊):資料分散的存儲在實體空間中,通過一根線儲存着它們之間的邏輯關系
- 單連結清單
- 雙連結清單
- 循環單連結清單
- 循環雙連結清單
下面詳細講解這兩種存儲結構 ????
3. 順序表
① 順序表定義
線性表的順序存儲。邏輯上相鄰的兩個元素在實體位置上也相鄰
數組就是順序表,下标一般從 0 開始:
順序表的特點:
- 随機通路(通過首位址和元素序号可在時間 O(1) 内找到元素)
- 插入和删除需要移動大量元素
- 存儲密度高,每個結點隻存儲資料元素
② 順序表基本操作
Ⅰ 插入
在數組 a 的第 i 個位置 (下标 i-1) 插入元素 e
// 第i個元素及其之後的元素後移for (int j = a.length; j >= i; j--)
a[j] = a[j - 1];
a[i - 1] = e;
length++;複制代碼 - 最好情況:在表尾插入,時間複雜度 O(1)
- 最壞情況:在表頭插入,時間複雜度 O(n)
- 平均情況:時間複雜度 O(n)
Ⅱ 删除
删除數組 a 的第 i 個位置的元素
// 從第 i 個位置元素前移for(int j = i; j < a.length; j++)
a[j-1] = a[j];
length --;複制代碼 - 最好情況:删除表尾元素,時間複雜度 O(1)
- 最壞情況:删除表頭元素,時間複雜度 O(n)
Ⅲ 按值查找
查找數組 a 中值為 e 的元素的下标
for (int i = 0; i < a.length; i++)if (a[i] == e)return i;複制代碼 - 最好情況:查找元素在表頭,時間複雜度 O(1)
- 最壞情況:查找元素在表尾,時間複雜度 O(n)
4. 連結清單
① 連結清單的定義與結構
線性表的鍊式存儲。邏輯上相鄰的兩個元素在實體位置不一定也相鄰
例如,使用連結清單存儲 {1,2,3},資料的實體存儲狀态如下圖所示:
可以看到,上圖根本無法展現出各資料之間的邏輯關系。對此,連結清單的解決方案是,每個資料元素在存儲時都配備一個指針,用于指向自己的直接後繼元素。如下圖所示:
當然,指針可以指向自己的直接後繼元素,也可以指向自己的直接前驅元素。為此,連結清單可分為:
- 單連結清單(指針指向自己的直接後繼元素)
- 雙連結清單(指針指向自己的直接後繼元素和直接前驅元素)
- 循環單連結清單(指針指向自己的直接後繼元素,表尾節點的指針指向頭節點)
- 循環雙連結清單(指針指向自己的直接後繼元素和直接前驅元素,表尾節點的指針指向頭節點)
通過以上大家應該也知道了,連結清單中每個資料的存儲都由以下兩部分組成:
- 資料域:資料元素本身
- 指針域:指向該元素直接後繼/前驅/...元素的指針
上圖所示的結構在連結清單中稱為節點。也就是說,連結清單實際存儲的是一個一個的節點,真正的資料元素包含在這些節點中,舉個單連結清單的例子:
???? 當然,上所示的連結清單結構并不完整。一個完整的連結清單需要由以下幾部分構成:
- 頭指針:一個普通的指針,它的特點是永遠指向連結清單第一個節點的位置。很明顯,頭指針用于指明連結清單的位置,便于後期找到連結清單并使用表中的資料
- 節點:連結清單中的節點又分為頭節點、首元節點和其他節點
- 頭節點:其實就是一個不存任何資料的空節點,通常作為連結清單的第一個節點。對于連結清單來說,頭節點不是必須的,它的作用隻是為了友善解決某些實際問題
- 首元節點:由于頭節點(也就是空節點)的緣故,連結清單中稱第一個存有資料的節點為首元節點。首元節點隻是對連結清單中第一個存有資料節點的一個稱謂,用于和頭節點進行區分,沒有實際意義
- 其他節點:連結清單中其他的節點
是以,一個存儲 {1,2,3} 的完整單連結清單結構如圖所示:
???? 引入頭節點的優點:
- 連結清單的首元節點的操作與其他位置的元素操作一樣,無須進行特殊處理
- 無論連結清單是否為空,其頭指針都是指向頭節點的非空指針,空表和非空表的處理得到了統一
② 單連結清單
Ⅰ 定義
單連結清單就是指針指向自己的直接後繼元素的連結清單
以 Java 為例,我們自定義一個單連結清單結構:
public class Node{private T t;private Node next;
......
}複制代碼 單連結清單可以解決順序表需要大量連續存儲空間的缺點,但單連結清單附加指針域,也存在浪費存儲空間的缺點
單連結清單是非随機存儲的存儲結構:即不能直接找到表中某個特點的結點。需要從頭開始周遊。
單連結清單通路前驅的時間複雜度為 O(n),通路後繼 O(1)
Ⅱ 基本操作
頭插法
在頭節點 L 的後面插入節點 s,即 s 節點成為目前連結清單的首元節點
頭插法的讀入順序和生成順序相反
s.next = L.next;
L.next = s;複制代碼 尾插法
在連結清單最後一個節點 r 的後面插入節點 s,即 s 節點成為目前連結清單的最後一個節點
尾插法的讀入順序和生成順序相同
r.next = s;
r = s; // s 節點成為連結清單的最後一個節點複制代碼 插入節點
p 節點之後插入 s 節點
s.next = p.next;
p.next = s;複制代碼 删除節點
p 節點之後删除 q 節點
// 删除 p 之後的 q q = p.next;
p.next = q.next;複制代碼 ③ 雙連結清單
雙連結清單就是同時具有前驅指針和後繼指針的連結清單
雙連結清單通路前驅和後繼結點時間複雜度都是 O(1)
以 Java 為例,我們自定義一個雙連結清單結構:
public class Node{private T t;private Node next;private Node prior;
......
}複制代碼 上圖中 2、3 順序可調換
s.next = p.next;
p.next.prior = s;
p.next = s;
s.prior = p;複制代碼 删除 p 節點之後的 s 節點
p.next = s.next;
s.next.prior = p;複制代碼 ③ 循環單連結清單
循環單連結清單就是表尾節點的指針指向頭節點的單連結清單
判空條件:表尾結點的 next 是否是等于頭指針
④ 循環雙連結清單
循環雙連結清單就是表尾節點的指針指向頭節點的雙連結清單
5. 順序表和連結清單的比較
1)存取方式
- 順序表可以順序存取,也可以随機存取
- 連結清單隻能從表頭順序存取元素
2)邏輯結構與實體結構
- 順序存儲時,邏輯上相鄰的元素,對應的實體存儲位置也相鄰
- 鍊式存儲時,邏輯上相鄰的元素,實體存儲位置不一定相鄰,其邏輯關系是通過指針連結來表示的
3)查找、插入和删除操作
-
對于按值查找,順序表無序時,兩者的時間複雜度均為 O(n);順序表有序時,可采用折半查找,此時的時間複雜度為 O(log2n)
對于按序号查找,順序表支援随機通路,時間複雜度僅為 O(1),而連結清單的平均時間複雜度為 O(n)。
-
順序表的插入、删除操作,平均需要移動半個表長的元素
連結清單的插入、删除操作,隻需要修改相關結點的指針域既可。由于連結清單的每個結點都有指針域,是以在存儲空間上要比順序表付出的代價大,存儲密度不夠大。
4)空間配置設定
-
順序存儲在靜态存儲配置設定情況下,一旦存儲空間裝滿就不能擴充,若再加入新元素,則會出現溢出,是以需要預先配置設定足夠大的存儲空間。預先配置設定過大,可能會導緻順序表候補大量閑置;預先配置設定過小,又會造成溢出。
動态存儲配置設定雖然存儲空間可以擴充,但需要移動大量元素,導緻操作效率降低,而且若記憶體中沒有更大的連續存儲空間,則會導緻配置設定失敗