深入浅出DFS(回溯),动态规划
1.基础
1.1问题抛出
数据结构老师曾经问过这样的问题:
是人脑聪明还是计算机聪明?
这是一个简单且引人深思的问题。要回答这个问题,我觉得我们首先应该思考计算机与人的大脑各自的特点。
计算机:
- 内存容量大。
- cpu计算频率快。
计算机擅长做的事情是计算,即做重复的事。
所以,能用编程的方法解决的问题通常 结构相同,问题规模不同。因此,我们解决一个问题的时候,通常需要将问题一步一步进行拆解,把一个大问题拆解为结构相同的若干个小问题。
而人脑,就是利用计算机的特点与数学模型,运用数据结构与算法,操作计算机去解决人不能解决的问题。
1.2解决重复问题的思路(回溯适用)###
- 1.状态与状态空间
为了解释状态的内涵,我拿递归举个例子。
我们在编程中常用的,最简单,易读,易维护的解决重复问题的方法便是使用递归。比如,在求斐波那契数列,写一个快速排序,归并排序,遍历二叉树。我们总能在递归调用里找到分治的影子。
大家一定知道,每一次递归调用,递归函数的参数一定有所变化,不然如何判断函数结束?不然意义何在?在算法的世界里,我们把每一次调用递归函数那个变化的参数叫做状态变量。
状态,代表着问题的规模,问题所处的阶段,是我们解决一个问题的程度。
人们说:递归分两步,第一步:结束条件;第二步:操作。当函数参数,或者某一个变量达到了一定规模,递归就会自动结束。这其实就是说,前面的递归操作,状态不断向着结束逼近,在这一步的递归执行,状态达到了结束条件。
解决重复性问题,脑海里一定要建立一个状态空间,状态空间就是状态的全集。这是对一个问题解决的宏观把控。
- 2.抽象树
虽然不同的状态是离散的,但是他们之间具有联系。我们可以把某种规模的问题描述想象成一个结点。由于规模相近的问题之间存在联系,我们把有联系的结点之间使用一条边连接,因此形成的状态空间就是一张图。
树结构有唯一的起始结点(根结点),从树的根节点开始,我们把一整个问题拆分成多个子问题,并且继续拆分的子问题没有相同的部分,回溯绝大多数问题的状态空间是一棵树。
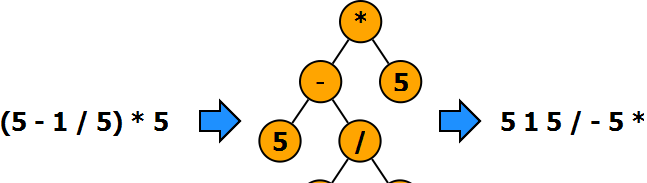
就比如我们在做四则运算的时候,可不可以将算式抽象成一棵树呢?
1.3递推(动态规划适用)
一个序列的递归定义指定了一个或多个初始的项以及一个由前项确定后项的规则,从前项求后项的规则就叫做递推关系。
————《离散数学及其应用(第8版)》
学习递推关系作用很大,解决了前后项的递推关系,编写递归程序的思路会十分清晰。事实上,动态规划问题就是在确立递推关系模型的基础上(最优子结构),建立起状态转移方程,从而求解。
下面我摘抄一道例题:
对于两个不含2个连续0的n位比特串个数,找出递推关系与初始条件。有多少个这样的5位比特串?
2.DFS(回溯)问题
DFS(回溯)问题的特点
DFS: deep first search。
正如其名,dfs本质上是一搜索,遍历是其手段,搜索是其目的。遍历是得到问题全解的手段。因此,dfs问题往往会让我们得到一个全集。让我们得到一个全解。
在遍历树时,会面临不同的道路与选择,我们的目的是走遍所有的路,那么当一条路走到尽头就要回到上一个路口,选择一条截然不同的路。
而回溯就是 深度优先遍历 状态空间的过程中发现的特有的现象,程序会回到以前访问过的结点。而程序在回到以前访问过的结点的时候,就需要将状态变量恢复成为第一次来到该结点的值。
回溯问题代码框架:
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表
DFS回溯经典问题——全排列
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/permutations
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
要解决这道题,我们的思维要进行如下几步:
- 1.抽象树
- 2.分析其状态空间。
- 3.确定我们要如何选择。
我们先把问题抽象成一颗树。我们在抽象问题成树的时候,要符合计算机的思维。抽象树的过程是把一个问题分解成重复子问题的过程。
请观察这个抽象树。在这道题中,每个节点的深度代表了完成问题的不同阶段。深度为0的节点是我们选择第一位数字的情况,深度为1的节点是我们选择第二的数字的情况。
于是,只需要按照数学中惯用的排列组合思维,就可以将这颗树轻松的画出。而且,这种不断取下一位作为节点去讨论的方法在解题中十分常见,符合计算机处理问题的习惯。
下面着重讲一讲什么叫,为什么,怎么样去“回溯”。
从 [1, 2, 3] 到 [1, 3, 2] ,深度优先遍历是这样做的,从 [1, 2, 3] 回到 [1, 2] 的时候,需要撤销刚刚已经选择的数 3,因为在这一层只有一个数 3 我们已经尝试过了,因此程序回到上一层,需要撤销对 2 的选择,好让后面的程序知道,选择 3 了以后还能够选择 2。这种令程序回到上一步,并把当前状态变量修改为上一步的状态变量的操作就叫做回溯。
那我们为什么要回溯呢?大家可以想想,如果不进行回溯,会发生什么?其实,我们在编写这道题的程序时,与其说在“遍历”抽象树,倒不如说在实现与生成自己心中抽象来的树。只不过我们生成树的方式比较特别,是按照递归,从底向上去生成的。那既然这样,当我们回到上一步节点时,如果我们不把状态变量恢复到上一步,那么这颗树就会被改变,因此生成树的操作就会失败。所以必须回溯。
现在我们就来具体的看下代码,这道题是如何回溯的。
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> ans;
backTrace(nums,ans,0,nums.size());
return ans;
}
void backTrace(vector<int> &nums,vector<vector<int>>& ans,int first,int size){//first为状态变量。
if(first==size){//判断状态变量是否达到结束条件。
ans.emplace_back(nums);
return;
}
for(int i=first;i<size;i++){//使用for循环遍历子节点
swap(nums[first],nums[i]);//使当前位置的数字改变。
backTrace(nums,ans,first+1,size);
swap(nums[i],nums[first]);//回溯
}
}
};
更聪明的回溯-剪枝
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/permutations-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。5
这道题与上一道题有什么不同呢? 全排列 的基础上增加了 序列中的元素可重复 这一条件,但要求:返回的结果又不能有重复元素。
那么我们的思路是:在遍历的过程中,一边遍历一遍检测,在一定会产生重复结果集的地方剪枝。
所以解题思路就很好确定,那就是去重。
class Solution {
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<vector<int>> vec;
int size=nums.size();
backTrack(vec,nums,size,0);
return vec;
}
void backTrack(vector<vector<int>> &vec,vector<int>& nums,int size,int first)
{
unordered_map<int,bool> map;
for(int i=0;i<size;i++)
{
map.emplace(nums[i],false);
}
if(first==size){
vec.push_back(nums);
return;
}
for(int i=first;i<size;i++){
if(!map.at(nums[i])){
swap(nums[i],nums[first]);
backTrack(vec,nums,size,first+1);
swap(nums[i],nums[first]);
map.erase(nums[i]);
map.emplace(nums[i],true);
}
}
}
};
但是大家千万不要像我这样写,每次递归都要建一个map,虽然思路正确但是效率极低。这样写只是为了可以更好的理解(懒+笨)。具体怎样去重其实有很多巧妙的办法,如果有时间可以仔细想想。
更多关于dfs(回溯)的练习
力扣:37,22,17,784,51,
DP问题
在动态规划问题中,我们将继续贯彻将原问题分解成为重复子问题的解题策略,但是不同的是,这次我们讨论的是子问题与原问题的关系。
DP问题特点
- 1.问法大多是求最优解。既是需要解决子问题,并通过子问题的组合得到原问题的最优解。
- 2.可通过递推求子问题以解决整个问题。在DP问题中,递推关系的表达形式为状态转移方程。
- 3.子问题具有无后效性。意为后续子问题不影响当前子问题的最优性。
解决DP问题的方法
解决DP问题,最重要的是解决子问题与原问题的关系。来看一道例题。
DP经典问题——300.最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-increasing-subsequence
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/dong-tai-gui-hua-er-fen-cha-zhao-tan-xin-suan-fa-p/
这篇是比较推荐的题解。看完题解后:请思考如下问题:
- 1.这个题目的状态定义是什么?
- 2.不同状态之间的关系是什么?
- 3.本题的子问题是否具有后效性?
- 4.本题的求解最优解过程是否用到了整个状态空间?
另一种DP问题
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/house-robber
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
https://leetcode-cn.com/problems/house-robber/solution/da-jia-jie-she-by-leetcode-solution/
请看完题解后,思考本题与上一道题的区别。
本题的求解最优解的过程与上一题有何不同?
总结
dfs问题与dp问题本质上都是将原问题分解以求解子问题的过程。
- 共同点