深入淺出DFS(回溯),動态規劃
1.基礎
1.1問題抛出
資料結構老師曾經問過這樣的問題:
是人腦聰明還是計算機聰明?
這是一個簡單且引人深思的問題。要回答這個問題,我覺得我們首先應該思考計算機與人的大腦各自的特點。
計算機:
- 記憶體容量大。
- cpu計算頻率快。
計算機擅長做的事情是計算,即做重複的事。
是以,能用程式設計的方法解決的問題通常 結構相同,問題規模不同。是以,我們解決一個問題的時候,通常需要将問題一步一步進行拆解,把一個大問題拆解為結構相同的若幹個小問題。
而人腦,就是利用計算機的特點與數學模型,運用資料結構與算法,操作計算機去解決人不能解決的問題。
1.2解決重複問題的思路(回溯适用)###
- 1.狀态與狀态空間
為了解釋狀态的内涵,我拿遞歸舉個例子。
我們在程式設計中常用的,最簡單,易讀,易維護的解決重複問題的方法便是使用遞歸。比如,在求斐波那契數列,寫一個快速排序,歸并排序,周遊二叉樹。我們總能在遞歸調用裡找到分治的影子。
大家一定知道,每一次遞歸調用,遞歸函數的參數一定有所變化,不然如何判斷函數結束?不然意義何在?在算法的世界裡,我們把每一次調用遞歸函數那個變化的參數叫做狀态變量。
狀态,代表着問題的規模,問題所處的階段,是我們解決一個問題的程度。
人們說:遞歸分兩步,第一步:結束條件;第二步:操作。當函數參數,或者某一個變量達到了一定規模,遞歸就會自動結束。這其實就是說,前面的遞歸操作,狀态不斷向着結束逼近,在這一步的遞歸執行,狀态達到了結束條件。
解決重複性問題,腦海裡一定要建立一個狀态空間,狀态空間就是狀态的全集。這是對一個問題解決的宏觀把控。
- 2.抽象樹
雖然不同的狀态是離散的,但是他們之間具有聯系。我們可以把某種規模的問題描述想象成一個結點。由于規模相近的問題之間存在聯系,我們把有聯系的結點之間使用一條邊連接配接,是以形成的狀态空間就是一張圖。
樹結構有唯一的起始結點(根結點),從樹的根節點開始,我們把一整個問題拆分成多個子問題,并且繼續拆分的子問題沒有相同的部分,回溯絕大多數問題的狀态空間是一棵樹。
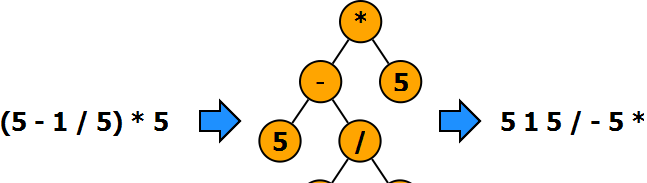
就比如我們在做四則運算的時候,可不可以将算式抽象成一棵樹呢?
1.3遞推(動态規劃适用)
一個序列的遞歸定義指定了一個或多個初始的項以及一個由前項确定後項的規則,從前項求後項的規則就叫做遞推關系。
————《離散數學及其應用(第8版)》
學習遞推關系作用很大,解決了前後項的遞推關系,編寫遞歸程式的思路會十厘清晰。事實上,動态規劃問題就是在确立遞推關系模型的基礎上(最優子結構),建立起狀态轉移方程,進而求解。
下面我摘抄一道例題:
對于兩個不含2個連續0的n位比特串個數,找出遞推關系與初始條件。有多少個這樣的5位比特串?
2.DFS(回溯)問題
DFS(回溯)問題的特點
DFS: deep first search。
正如其名,dfs本質上是一搜尋,周遊是其手段,搜尋是其目的。周遊是得到問題全解的手段。是以,dfs問題往往會讓我們得到一個全集。讓我們得到一個全解。
在周遊樹時,會面臨不同的道路與選擇,我們的目的是走遍所有的路,那麼當一條路走到盡頭就要回到上一個路口,選擇一條截然不同的路。
而回溯就是 深度優先周遊 狀态空間的過程中發現的特有的現象,程式會回到以前通路過的結點。而程式在回到以前通路過的結點的時候,就需要将狀态變量恢複成為第一次來到該結點的值。
回溯問題代碼架構:
for 選擇 in 選擇清單:
# 做選擇
将該選擇從選擇清單移除
路徑.add(選擇)
backtrack(路徑, 選擇清單)
# 撤銷選擇
路徑.remove(選擇)
将該選擇再加入選擇清單
DFS回溯經典問題——全排列
給定一個 沒有重複 數字的序列,傳回其所有可能的全排列。
示例:
輸入: [1,2,3]
輸出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
來源:力扣(LeetCode)
連結:https://leetcode-cn.com/problems/permutations
著作權歸領扣網絡所有。商業轉載請聯系官方授權,非商業轉載請注明出處。
要解決這道題,我們的思維要進行如下幾步:
- 1.抽象樹
- 2.分析其狀态空間。
- 3.确定我們要如何選擇。
我們先把問題抽象成一顆樹。我們在抽象問題成樹的時候,要符合計算機的思維。抽象樹的過程是把一個問題分解成重複子問題的過程。
請觀察這個抽象樹。在這道題中,每個節點的深度代表了完成問題的不同階段。深度為0的節點是我們選擇第一位數字的情況,深度為1的節點是我們選擇第二的數字的情況。
于是,隻需要按照數學中慣用的排列組合思維,就可以将這顆樹輕松的畫出。而且,這種不斷取下一位作為節點去讨論的方法在解題中十分常見,符合計算機處理問題的習慣。
下面着重講一講什麼叫,為什麼,怎麼樣去“回溯”。
從 [1, 2, 3] 到 [1, 3, 2] ,深度優先周遊是這樣做的,從 [1, 2, 3] 回到 [1, 2] 的時候,需要撤銷剛剛已經選擇的數 3,因為在這一層隻有一個數 3 我們已經嘗試過了,是以程式回到上一層,需要撤銷對 2 的選擇,好讓後面的程式知道,選擇 3 了以後還能夠選擇 2。這種令程式回到上一步,并把目前狀态變量修改為上一步的狀态變量的操作就叫做回溯。
那我們為什麼要回溯呢?大家可以想想,如果不進行回溯,會發生什麼?其實,我們在編寫這道題的程式時,與其說在“周遊”抽象樹,倒不如說在實作與生成自己心中抽象來的樹。隻不過我們生成樹的方式比較特别,是按照遞歸,從底向上去生成的。那既然這樣,當我們回到上一步節點時,如果我們不把狀态變量恢複到上一步,那麼這顆樹就會被改變,是以生成樹的操作就會失敗。是以必須回溯。
現在我們就來具體的看下代碼,這道題是如何回溯的。
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> ans;
backTrace(nums,ans,0,nums.size());
return ans;
}
void backTrace(vector<int> &nums,vector<vector<int>>& ans,int first,int size){//first為狀态變量。
if(first==size){//判斷狀态變量是否達到結束條件。
ans.emplace_back(nums);
return;
}
for(int i=first;i<size;i++){//使用for循環周遊子節點
swap(nums[first],nums[i]);//使目前位置的數字改變。
backTrace(nums,ans,first+1,size);
swap(nums[i],nums[first]);//回溯
}
}
};
更聰明的回溯-剪枝
給定一個可包含重複數字的序列 nums ,按任意順序 傳回所有不重複的全排列。
示例 1:
輸入:nums = [1,1,2]
輸出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
輸入:nums = [1,2,3]
輸出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
來源:力扣(LeetCode)
連結:https://leetcode-cn.com/problems/permutations-ii
著作權歸領扣網絡所有。商業轉載請聯系官方授權,非商業轉載請注明出處。5
這道題與上一道題有什麼不同呢? 全排列 的基礎上增加了 序列中的元素可重複 這一條件,但要求:傳回的結果又不能有重複元素。
那麼我們的思路是:在周遊的過程中,一邊周遊一遍檢測,在一定會産生重複結果集的地方剪枝。
是以解題思路就很好确定,那就是去重。
class Solution {
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<vector<int>> vec;
int size=nums.size();
backTrack(vec,nums,size,0);
return vec;
}
void backTrack(vector<vector<int>> &vec,vector<int>& nums,int size,int first)
{
unordered_map<int,bool> map;
for(int i=0;i<size;i++)
{
map.emplace(nums[i],false);
}
if(first==size){
vec.push_back(nums);
return;
}
for(int i=first;i<size;i++){
if(!map.at(nums[i])){
swap(nums[i],nums[first]);
backTrack(vec,nums,size,first+1);
swap(nums[i],nums[first]);
map.erase(nums[i]);
map.emplace(nums[i],true);
}
}
}
};
但是大家千萬不要像我這樣寫,每次遞歸都要建一個map,雖然思路正确但是效率極低。這樣寫隻是為了可以更好的了解(懶+笨)。具體怎樣去重其實有很多巧妙的辦法,如果有時間可以仔細想想。
更多關于dfs(回溯)的練習
力扣:37,22,17,784,51,
DP問題
在動态規劃問題中,我們将繼續貫徹将原問題分解成為重複子問題的解題政策,但是不同的是,這次我們讨論的是子問題與原問題的關系。
DP問題特點
- 1.問法大多是求最優解。既是需要解決子問題,并通過子問題的組合得到原問題的最優解。
- 2.可通過遞推求子問題以解決整個問題。在DP問題中,遞推關系的表達形式為狀态轉移方程。
- 3.子問題具有無後效性。意為後續子問題不影響目前子問題的最優性。
解決DP問題的方法
解決DP問題,最重要的是解決子問題與原問題的關系。來看一道例題。
DP經典問題——300.最長遞增子序列
給你一個整數數組 nums ,找到其中最長嚴格遞增子序列的長度。
子序列是由數組派生而來的序列,删除(或不删除)數組中的元素而不改變其餘元素的順序。例如,[3,6,2,7] 是數組 [0,3,1,6,2,2,7] 的子序列。
示例 1:
輸入:nums = [10,9,2,5,3,7,101,18]
輸出:4
解釋:最長遞增子序列是 [2,3,7,101],是以長度為 4 。
示例 2:
輸入:nums = [0,1,0,3,2,3]
輸出:4
示例 3:
輸入:nums = [7,7,7,7,7,7,7]
輸出:1
來源:力扣(LeetCode)
連結:https://leetcode-cn.com/problems/longest-increasing-subsequence
著作權歸領扣網絡所有。商業轉載請聯系官方授權,非商業轉載請注明出處。
https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/dong-tai-gui-hua-er-fen-cha-zhao-tan-xin-suan-fa-p/
這篇是比較推薦的題解。看完題解後:請思考如下問題:
- 1.這個題目的狀态定義是什麼?
- 2.不同狀态之間的關系是什麼?
- 3.本題的子問題是否具有後效性?
- 4.本題的求解最優解過程是否用到了整個狀态空間?
另一種DP問題
你是一個專業的小偷,計劃偷竊沿街的房屋。每間房内都藏有一定的現金,影響你偷竊的唯一制約因素就是相鄰的房屋裝有互相連通的防盜系統,如果兩間相鄰的房屋在同一晚上被小偷闖入,系統會自動報警。
給定一個代表每個房屋存放金額的非負整數數組,計算你 不觸動警報裝置的情況下 ,一夜之内能夠偷竊到的最高金額。
示例 1:
輸入:[1,2,3,1]
輸出:4
解釋:偷竊 1 号房屋 (金額 = 1) ,然後偷竊 3 号房屋 (金額 = 3)。
偷竊到的最高金額 = 1 + 3 = 4 。
示例 2:
輸入:[2,7,9,3,1]
輸出:12
解釋:偷竊 1 号房屋 (金額 = 2), 偷竊 3 号房屋 (金額 = 9),接着偷竊 5 号房屋 (金額 = 1)。
偷竊到的最高金額 = 2 + 9 + 1 = 12 。
來源:力扣(LeetCode)
連結:https://leetcode-cn.com/problems/house-robber
著作權歸領扣網絡所有。商業轉載請聯系官方授權,非商業轉載請注明出處。
https://leetcode-cn.com/problems/house-robber/solution/da-jia-jie-she-by-leetcode-solution/
請看完題解後,思考本題與上一道題的差別。
本題的求解最優解的過程與上一題有何不同?
總結
dfs問題與dp問題本質上都是将原問題分解以求解子問題的過程。
- 共同點