义乌集训 2021.07.08 C
题目描述
输入一个 \(01\) 串 \(S1\)。你需要输出一个最短的 \(01\) 串 \(S2\),使得 \(S2\) 在 \(S1\) 中从未出现过。
如果有多个可行的解,你需要输出字典序最小的那一个。
数据范围
对于 \(10\%\) 的数据,满足输入数据为样例。
对于 \(30\%\) 的数据,满足 \(|S1|\le1000∣S1∣≤1000\)。
对于 \(50\%\) 的数据,满足 \(|S1|\le1000000∣S1∣≤1000000\)。
对于另外 \(20\%\) 的数据,时限为 \(2s\)。
对于 \(100\%\) 的数据,满足 \(1\le\left|S1\right|\le167772161≤∣S1∣≤16777216\)。
思路
注意到 \(S1\) 长度的范围有点诡异,用电脑自带的计算器算一下可以发现 \(2^{24}=16777216\)。再仔细一想。长度为 \(x\) 的字符串总共有 \(2^x\) 个,而长度为 \(n\) 原串能提供的长度为 \(x\) 的字符串最多只有 \(n-x+1\) 个,那么存在没有出现的长度为 \(x\) 的字串的充分条件就是 \(2^x>n-x+1\)。在 \(n=16777216\) 时,不等式显然也成立。那么就说明 \(S2\) 的长度不会超过 \(24\)。
也就可以二分 \(S2\) 的长度。
将 \(S1\) 中所有长度为 \(x\) 的子串记录到所有长度为 \(x\) 的字符串的集合中,遍历一遍集合,找到第一个没有出现过的字符串。如果存在,就继续二分判断是否存在长度更小的答案。反之则判断长度更大的字符串。
code:
#include<cstdio>
#include<cstring>
using namespace std;
const int N=16777220;
char s[N];
int m,ans,cnt[N],a[N];
bool check(int len)
{
int now=0;
int siz=(1<<len)-1;
for(int i=1;i<len;i++) now=(now<<1)+a[i];
// print(now,len);
for(int i=len;i<=m;i++) cnt[now=((now<<1)+a[i])&siz]=1;
for(int i=0;i<=siz;i++)
if(!cnt[i]) {return ans=i,true;}
for(int i=0;i<=siz;i++) cnt[i]=0;
return false;
}
int main()
{
scanf("%s",s+1);
m=strlen(s+1);
for(int i=1;i<=m;i++) a[i]=s[i]^48;
int l=1,r=24;
while(l<r)
{
int mid=l+r-1>>1;
if(check(mid)) r=mid;
else l=mid+1;
}
check(l);
for(int i=l-1;i>=0;i--) printf("%d",ans>>i&1);
return 0;
}
义乌集训 2021.07.08 D
题意
给定一个序列 \(A\),定义一个区间 \([l,r]\) 的最大子段和为 \([l,r]\) 的一段连续子区间的和,满足其为 \([l,r]\) 所有连续子区间和中最大的一个。
求出所有 $1≤l≤r≤n $的区间 \([l,r]\) 的最大子段和的和,答案对 \(2^{64}\) 取模。
对于 \(30\%\) 的数据,满足 \(1≤n≤1000\)。
对于另外 \(20\%\) 的数据,满足 \(0≤A_i\)
对于 \(100\%\) 的数据,满足 \(1 \leq n \leq 100000,-10^9 \leq A_i \leq 10^9\)。
朴素的做法为 \(O(n^3)\) ,因为最大子段和可以 \(O(n)\) 求。
而对于 \(A_i \leq 0\) 的部分分,任意一个数在所有包含他的区间中,对最大字段和都有贡献,即 \(i*(n-i+1)*A_i\)。
对于满分做法。需要用到的思想就是将最大子段和相同的区间一起求出来,而不是一个个枚举。那么就可以考虑分治。如下图所示,考虑如何在低于 \(O(n^3)\) 内求出所有区间对答案的贡献。
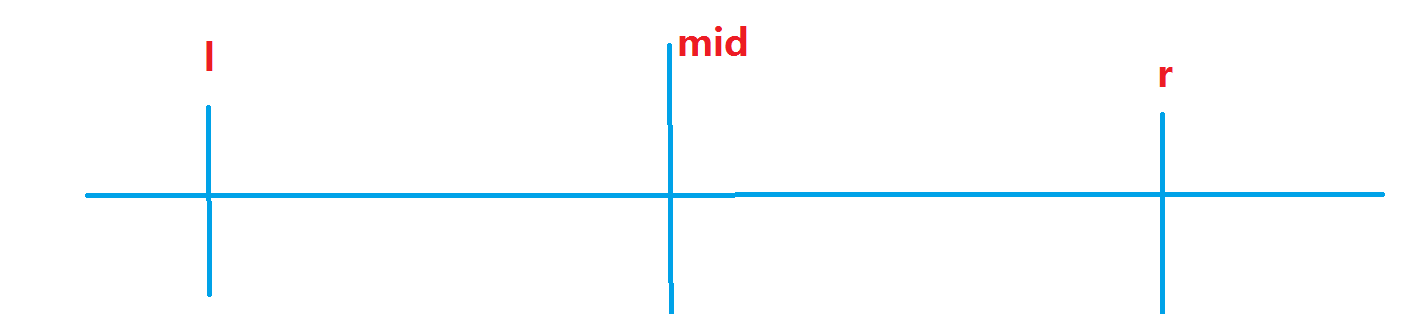
考虑对 \(mid\) 前面求最大后缀和 \(suf\) ,对 \(mid\) 后面求最大前缀和 \(pre\),这两个数组显然具有单调性。同时分别求出 \([i,mid](l\leq i \leq mid)\) 内的最大字段和 \(maxn_i\),以及\([mid+1,j](mid+1 \leq j \leq r)\) 内的最大字段和 \(maxn_j\)。
显然,\(maxn_i \geq suf_i\),那么区间最大值的取值就可以分为三类。
1.\(suf_i +pre_j\)
2.\(maxn_i\)
3.\(maxn_j\)
同时注意到,在左端点 \(i\) 固定时,\(suf_i\) 和 \(maxn_i\) 也是固定不变的,而 \(pre_j\) 则是非严格单调递增的。于是就可以枚举 \(i\),计算第 \(1\) 和第 \(2\) 种情况对答案的贡献,再枚举 \(j\),计算第 \(2\) 和第 \(3\) 种情况对答案的贡献。
以枚举 \(i\) 为例,首先将右端点右移到第一个满足 \(maxn_j' > maxn_i\),对于 \(j< j'\),那么显然 \(maxn_j\) 就不会是答案。此时再二分找到最后一个满足 \(suf_i+pre_j''\leq maxn_i\),那么 \(maxn_i\) 对于答案的贡献就是 \((j''-mid)*maxn_i\),而 \(suf_i+pre_j\) 对答案的贡献就是 \(\sum_{k=j''+1}^{j'-1}(suf_i+pre_k)\)。于是可以预处理出 \(pre_j\) 的前缀和。
最终的时间复杂度就是 \(O(n \log n)\)。
#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e5+10;
int n,a[N];
long long now,sum[N],maxn[N];
unsigned long long Q[N],ans;
void solve(int l,int r)
{
if(l==r)
{
ans+=a[l];
return ;
}
int m=(l+r)>>1,rs,lf,rf;
solve(l,m),solve(m+1,r);
sum[m]=maxn[m]=a[m],now=max(0,a[m]);
for(int i=m-1;i>=l;i--)
{
sum[i]=sum[i+1]+a[i];
now+=a[i];
maxn[i]=max(maxn[i+1],now);
now=max(now,0ll);
}
Q[m]=sum[m];
for(int i=m-1;i>=l;i--)
{
sum[i]=max(sum[i+1],sum[i]);
Q[i]=Q[i+1]+sum[i];
}
sum[m+1]=maxn[m+1]=a[m+1],now=max(0,a[m+1]);
for(int i=m+2;i<=r;i++)
{
sum[i]=sum[i-1]+a[i];
now+=a[i];
maxn[i]=max(maxn[i-1],now);
now=max(now,0ll);
}
Q[m+1]=sum[m+1];
for(int i=m+2;i<=r;i++)
{
sum[i]=max(sum[i],sum[i-1]);
Q[i]=Q[i-1]+sum[i];
}
Q[m]=0;
rs=m+1;
for(int i=m;i>=l;i--)
{
while(rs<=r&&maxn[rs]<=maxn[i]) rs++;
lf=m,rf=rs;
while(lf+1<rf)
{
int mid=(lf+rf)>>1;
if(sum[mid]<maxn[i]-sum[i]) lf=mid;
else rf=mid;
}
ans+=Q[rs-1]-Q[lf]+(rs-lf-1)*sum[i]+maxn[i]*(lf-m);
}
Q[m]=sum[m],Q[m+1]=0;
rs=m;
for(int i=m+1;i<=r;i++)
{
while(rs>=l&&maxn[rs]<maxn[i]) rs--;
lf=rs,rf=m+1;
while(lf+1<rf)
{
int mid=(lf+rf)>>1;
if(sum[mid]>maxn[i]-sum[i]) lf=mid;
else rf=mid;
}
ans+=Q[rs+1]-Q[rf]+(rf-rs-1)*sum[i]+maxn[i]*(m-lf);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
solve(1,n);
printf("%llu\n",ans);
return 0;
}
义乌集训 2021.07.09 D
你有一棵 \(n\) 节点的树 \(T\),回答 \(m\) 个询问,每次询问给你两个整数 \(l,r\) ,问存在多少个整数 \(k\) 使得从树上编号为 \(l\) 的点沿着 \(l\rightarrow r\) 的简单路径走 \(k\) 步恰好到达 \(k\) 。
首先转化一下题意,对于 \(l\) 到 \(r\) 的路径可以拆分成 \(l\rightarrow LCA(l,r)\) 和 \(LCA(l,r) \rightarrow r\)。同时需要注意不要将 \(LCA(l,r)\) 同时放在两边。
对于第一部分,就是求有多少个 \(k\) 满足 \(depth[l]-depth[k]=k\)。移项,也就是 \(depth[l]=k+depth[k]\)。
同理,对于第二部分,就是求有多少个 \(k\) 满足 \(depth[x]+depth[k]-2*depth[LCA(l,r)]=k\)。移项,也就是 \(depth[x]-2*depth[LCA(l,r)]=k-depth[k]\)。
然后就变成了和天天爱跑步类似的题目。代码实现也是类似的。
具体来说,记 \([x,y]\) 表示 \(x \rightarrow y\) 这条链上满足题意的 \(k\) 的数量。那么就可以将 \([LCA(l,r),r]\) 拆分成 \([1,r]-[1,fa[(LCA(l,r)]]\)。那么就可以将询问离线。再开一个桶记录当前链上所有满足题意的点,再在 \(fa[LCA(l,r)]\) 打上一个标记。对于第二部分同理。但是要注意 \(k-depth[k]\) 有可能小于 \(0\),所以需要加上一个 \(n\)。
#include<cstdio>
#include<vector>
#include<iostream>
using namespace std;
const int N=3e5+10;
const int M=3e5+10;
int h[N],idx,din[N],n,m,fa[N][25],depth[N],lg[N];
int x[N],y[N],z[N],f[N<<1],ans[N];
struct edge{
int v,nex;
}e[M<<1];
void add(int u,int v)
{
e[++idx].v=v;
e[idx].nex=h[u];
h[u]=idx;
}
struct query{
int id,x,flag;
};
vector<query> Q[N];
void dfs(int u,int father)
{
depth[u]=depth[father]+1,fa[u][0]=father;
for(int i=1;i<=lg[depth[u]];i++) fa[u][i]=fa[fa[u][i-1]][i-1];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v==father) continue;
dfs(v,u);
}
}
int LCA(int x,int y)
{
if(depth[x]<depth[y]) swap(x,y);
while(depth[x]>depth[y]) x=fa[x][lg[depth[x]-depth[y]]-1];
if(x==y) return x;
for(int i=lg[depth[x]];i>=0;i--)
if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
void get_ans1(int u,int father)
{
f[depth[u]+u]++;
for(int i=0;i<Q[u].size();i++)
{
query now=Q[u][i];
ans[now.id]+=f[now.x]*now.flag;
}
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v!=father) get_ans1(v,u);
}
f[depth[u]+u]--;
}
void get_ans2(int u,int father)
{
f[u-depth[u]+n]++;
for(int i=0;i<Q[u].size();i++)
{
query now=Q[u][i];
ans[now.id]+=f[now.x+n]*now.flag;
}
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v!=father) get_ans2(v,u);
}
f[u-depth[u]+n]--;
}
int main()
{
scanf("%d%d",&n,&m);
for(int u,v,i=1;i<n;i++)
{
scanf("%d%d",&u,&v);
add(u,v),add(v,u);
}
for(int i=1;i<N;i++) lg[i]=lg[i-1]+((1<<lg[i-1])==i);
dfs(1,0);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&x[i],&y[i]);
z[i]=LCA(x[i],y[i]);
Q[x[i]].push_back(query{i,depth[x[i]],1});
Q[fa[z[i]][0]].push_back(query{i,depth[x[i]],-1});
}
get_ans1(1,0);
for(int i=1;i<=n;i++) Q[i].clear();
for(int i=1;i<=m;i++)
{
Q[y[i]].push_back(query{i,depth[x[i]]-2*depth[z[i]],1});
Q[z[i]].push_back(query{i,depth[x[i]]-2*depth[z[i]],-1});
}
get_ans2(1,0);
for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
return 0;
}
义乌集训 2021.7.10 C
给你一个长为 \(n\) 的序列 \(a\) 和一个常数 \(k\)。 有 \(m\) 次询问,每次查询一个区间 \([l,r]\) 内所有数最少分成多少个连续段,使得每段的和都 \(\le k\)。 如果这一次查询无解,输出 "Chtholly",输出的字符串不包含引号。
首先有一个贪心性质,对于以每个点为起点的段,显然要把所有能放下的数都放进来。在满足上面贪心的前提下,对于每一个区间 \([x,y]\),可以从 \(x\) 向 \(y+1\) 连一条边,那么除了最后一个点,每个点都会向后连一条边。于是问题就转化为了 \(l\) 在树上跳多少步可以跳到比 \(r+1\) 深度更低的地方。显然可以用倍增求解。复杂度为 \(O(n \log n)\),复杂度瓶颈在连边上。
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e6+10;
#define LL long long
int idx,n,m,k,fa[N][30],h[N],b[N];
LL a[N],sum[N];
int main()
{
scanf("%d%d%lld",&n,&m,&k);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]),sum[i]=sum[i-1]+a[i];
for(int i=1;i<=n;i++)
{
b[i]=b[i-1]+(a[i]>k);
int l=i+1,r=n+1;
while(l<r)
{
int mid=l+r>>1;
if(sum[mid]-sum[i-1]>k) r=mid;
else l=mid+1;
}
// r=upper_bound(sum+1,sum+n+1,sum[i-1]+k)-sum;
fa[i][0]=r;
}
for(int i=0;i<=20;i++) fa[n+1][i]=n+1;
for(int u=n;u>=1;u--)
for(int i=1;i<=20;i++)
fa[u][i]=fa[fa[u][i-1]][i-1];
while(m--)
{
int l,r;
scanf("%d%d",&l,&r);
if(b[r]-b[l-1]>0)
{
puts("Chtholly");
continue;
}
int ans=0;
while(l<=r)
{
int k=20;
for(k=20;k>=0;k--)
{
if(fa[l][k]<=r)
{
l=fa[l][k],ans+=1<<k;
break;
}
}
if(fa[l][0]>r)
{
l=fa[l][0];
ans++;
}
}
printf("%d\n",ans);
}
return 0;
}
义乌集训 2021.07.10 D
给定一棵 \(n\) 个节点的树,第 \(i\) 个点的编号为 \(i\),第 \(j\) 条边的编号为 \(j\)。 有 \(m\) 次查询,每次给出 \(l,r\),查询如果只保留树上点编号在 \([l,r]\) 内的点,边编号在 \([l,r]\) 内的边,有多少点连通块, 此时点 \(a\) 与 \(b\) 连通等价于\(l≤a,b≤r\) 且 \(a,b\) 在树上的简单路径中所有点与边编号都在 \([l,r]\) 之间。
对于其中 \(30\%\) 的数据,\(n,m \leq 1000\)
对于其中 \(50\%\) 的数据,\(n \leq 1000\)
对于另外 \(20\%\) 的数据,\(n,m \leq 100000\)
对于全部数据,$1 \leq n,m \leq 1000000 $
首先,本题有一个结论:连通块数 \(=\) 点数 \(-\) 边数。因为对于本题来说,每连一条边就会合并两个连通块。
那么对于 \([l,r]\) ,点数是确定的。那么现在就是要求边数,而一条连接 \(u\) 和 \(v\) 的边 \(i \in [l,r]\),当且仅当 \(l \leq \min(u,v,i) \leq \max(u,v,i) \leq r\)。于是就可以将询问离线。再将边按照 \(\max(u,v,i)\) 排序,再将 \(\min(u,v,i)\) 存入树状数组中,在询问时输出 \(query(r)-query(l-1)\) 即可。
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1e6+10;
const int M=1e6+10;
int lowbit(int x){return x&(-x);}
struct edge{
int minv,maxv;
bool operator <(const edge &t)const{
return maxv<t.maxv;
}
}e[M];
struct NLC{
int l,r,id,ans;
bool operator <(const NLC &t)const{
return r<t.r;
}
}q[M];
bool cmp(NLC a,NLC b){return a.id<b.id;}
int n,m,c[N];
void add(int x,int k)
{
while(x<=n)
{
c[x]+=k;
x=x+lowbit(x);
}
}
int query(int x)
{
int res=0;
while(x)
{
res+=c[x];
x-=lowbit(x);
}
return res;
}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
int main()
{
scanf("%d%d",&n,&m);
for(int u,v,i=1;i<n;i++)
{
scanf("%d%d",&u,&v);
e[i].minv=min(min(u,v),i);
e[i].maxv=max(max(u,v),i);
}
sort(e+1,e+n);
for(int i=1;i<=m;i++) scanf("%d%d",&q[i].l,&q[i].r),q[i].id=i;
sort(q+1,q+m+1);
int now=1;
for(int i=1;i<=m;i++)
{
while(e[now].maxv<=q[i].r&&now<n) add(e[now++].minv,1);
q[i].ans=(q[i].r-q[i].l+1)-(query(q[i].r)-query(q[i].l-1));
}
sort(q+1,q+m+1,cmp);
for(int i=1;i<=m;i++) printf("%d\n",q[i].ans);
return 0;
}
义乌集训 2021.07.11 C
给定一张图,保证每个点最多属于一个简单环,每个点度数最多为 \(3\) ,求这个图有多少“眼镜图形”。 其中“眼镜图形”,定义为三元组 \((x,y,S)\),其中 \(x\) 和 \(y\) 表示图上的两个点,\(S\) 表示一条 \(x\) 到 \(y\) 的简单路径,而且必须满足:
1.\(x\) 和 \(y\) 分别在两个不同的简单环上
2.\(x\) 所在的简单环与路径 \(S\) 的所有交点仅有 \(x\)。\(y\) 所在的简单环与路径 \(S\) 的所有交点仅有 \(y\)。
\((x,y,S)\) 与 \((y,x,S)\) 算同一个眼镜。
下图标明了所有的“眼镜图形”。
保证图联通。
对于图中出现的简单环,显然首先需要缩点,而本图中是无向图,和有向图中的缩点有一些细节上的差异。
而缩点之后的图就不存在简单环了,那么也就必然是一棵树。于是可以考虑树形 dp,对眼镜进行分类讨论。
设 \(f[i]\) 表示 \(i\) 所在的子树能够提供给除了该子树外的其他部分的路径数。
显然,当 \(i\) 是普通的点时,\(f[i]=\sum_{j \in son(i)} f[j]\)。
而当 \(i\) 是缩点后的环时,\(f[i]=(2*\sum_{j \in son(j)}f[j])+1\)。因为子树内可以通过 \(i\) 的两边走出去。同时自己也能提供一条路径。
对于答案统计,每个点可以只统计在他子树内的路径。而如果它是环,那么也能作为另一个端点。即,如果 \(i\) 是环,那么 \(ans+=\sum_{j \in son(i)}\)。
而如果 \(i\) 作为路径的中间部分,也就是 \(i\) 子树内的两条路径在 \(i\) 处连接上。如下图所示:
对于这种情况,\(ans+=\sum_{j \in son(i)}\sum_{k \in son(i) \cap k \ne i}f[j]*f[k]\)。
如果用 \(a,b,c,d...\) 来表示 \(f[j]\),那么 \(ans+=ab+bc+cd+ad\)。而 \((a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2bc+2cd+2ad\)。那么就可以预处理出 \(f[j]\) 的和 \(s\),以及 \(f[j]\) 和的平方 t。那么 \(ans+=(s^2-t)/2\)。
因为答案要对 \(19260817\) 取模,所以这里需要乘以 \(2\) 在模 \(19260817\) 意义下的乘法逆元。
同时需要注意,如果当前点是环,那么两个子树内部的路径同样可以在 \(i\) 中通过两个方向连接。即 \(ans+=(s^2-t)\)。
#include<cstdio>
#include<stack>
#include<map>
using namespace std;
const int N=1e6+10;
const int M=4e6+10;
#define int long long
const int mod=19260817;
int n,m,rh[N],h[N],idx;
struct edge{
int v,nex;
}e[M<<1];
int id[N],ans,f[N],num,scc_cnt,siz[N],dfn[N],low[N],din[N];
bool st[N];
stack<int> s;
int min(int a,int b){return a<b?a:b;}
int max(int a,int b){return a>b?a:b;}
void add(int h[],int u,int v)
{
e[++idx].v=v;
e[idx].nex=h[u];
h[u]=idx;
}
int qmul(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=(a*a)%mod;
b>>=1;
}
return res;
}
void tarjan(int u,int fa)
{
dfn[u]=low[u]=++num;
s.push(u),st[u]=true;
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa) continue;
if(!dfn[v])
{
tarjan(v,u);
low[u]=min(low[u],low[v]);
}
else if(st[v]) low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u])
{
int y;
scc_cnt++;
do{
y=s.top();s.pop();
st[y]=false;
siz[scc_cnt]++;
id[y]=scc_cnt;
} while(y!=u);
}
}
void dfs(int u,int fa)
{
int res=0ll,son=0ll;
int mul=0ll;
for(int i=rh[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa) continue;
dfs(v,u);
son++;
f[u]=(f[u]+f[v])%mod;
res=(res+f[v])%mod;
mul=(mul+f[v]*f[v]%mod)%mod;
}
res=res*res%mod;
res=((res-mul)*qmul(2,mod-2)%mod+mod)%mod;
ans=(ans%mod+res*(siz[u]>1ll?2ll:1ll)%mod)%mod;
if(siz[u]>1ll)
{
ans=(ans+f[u])%mod;
f[u]=f[u]*2ll%mod+1ll;
}
f[u]%=mod;
}
signed main()
{
scanf("%lld%lld",&n,&m);
for(int u,v,i=1ll;i<=m;i++)
{
scanf("%lld%lld",&u,&v);
add(h,u,v),add(h,v,u);
}
tarjan(1ll,-1ll);
for(int u=1ll;u<=n;u++)
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
int a=id[u],b=id[v];
if(a==b) continue;
add(rh,a,b);
}
dfs(1ll,-1ll);
printf("%lld\n",(ans%mod+mod)%mod);
return 0;
}
义乌集训 2021.07.12 A
给定序列 \(a_1,a_2,a_3 \dots a_n\),算出 \(t_1,t_2,\dots t_n\) 满足
1.\(\forall t_i >0\);
2.\(\forall i \in[1,n),a_i*a_{i+1}*t_i*t_{i+1}\) 是完全平方数;
3.\(\prod t_i\) 最小。
求出\(\prod t_i\) ,答案对 \(1e9+7\) 取模。
看到完全平方数,首先想到就是分解质因数,分解后就可以对不同数值的质因子单独考虑。对于出现偶数次的质因子,本身就是一个完全平方数,在此处就可以当它没有出现过。而对于出现了奇数次的质因子,可以用 \(01\) 序列表示这个质因子是否在这个数中出现过奇数次。
如 \(2\) 在 \(10,12,8,7,6\) 这个序列中的 \(01\) 串即为 \(10001\)。而现在想要把相邻的两个数相乘变成一个完全平方数,显然有两种方案:
1.把所有的 \(1\) 变成 \(0\),即让该质因子在每一个 \(a_i*t_i\) 中都出现过偶数次,那么相邻的两个数就一定也出现过偶数次,也就是必然是一个完全平方数。
2.把所有的 \(1\) 变成 \(0\),那么虽然 \(a_i*t_i\) 不能完全开方,但该质因子在 \(a_i*t_i*a_{i+1}*t_{i+1}\) 中也就一定出现了偶数次,那么也满足题意。
而现在要求 \(\prod t_i\) 最小,也就是新添加的质因子之积最小。设 \(p_i\) 的 \(01\) 序列有 \(cnt\) 个 \(1\),那么 \(ans*=p_i^{\min(cnt,n-cnt)}\)。
应该都会用快速幂吧。
#include<cstdio>
using namespace std;
const int N=1e6+10;
#define int long long
const int mod=1e9+7;
int num[N],n,ans=1;
int min(int a,int b){return a<b?a:b;}
int mul(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
signed main()
{
scanf("%lld",&n);
for(int x,i=1;i<=n;i++)
{
scanf("%lld",&x);
for(int k=2;k*k<=x;k++)
{
int cnt=0;
if(x%k==0)
{
while(x%k==0) cnt++,x/=k;
num[k]+=cnt&1;
}
}
if(x>1) num[x]++;
}
for(int i=2;i<=1e6;i++) ans=ans*mul(i,min(num[i],n-num[i]))%mod;
printf("%lld\n",ans%mod);
return 0;
}
义乌集训 2021.07.12 B
有一个 \(n×m\) 的棋盘。初始每个格子都是好的,之后每一秒会坏一个之前没坏的格子。\(nm\) 秒过后所有格子都会坏完。
我们想知道,每一秒过后,有多少子矩形满足其中的所有格子都是好的。
对于所有数据,\(1\leq n,m \leq 500\)。
每一次破坏都会减少一些格子,但是这样子不太好计算。可以利用一种非常巧妙的方法,将题目转化为初始时所有格子都是坏的,再将格子一个一个变好。这样就可以方便计算了,在输出时直接逆序输出即可。
如下图所示
红色的格子表示现在是坏的格子,蓝色的格子表示是当前变好的格子,绿色的格子表示当蓝色的格子变好时,不会对答案产生贡献的好的格子。黄色箭头表示向四个方向最远能到达的格子。
对于快速求出四个方向能到达的点,可以用一种类似于并查集的思想,用 \(f[i][j][0]\) 表示 \((i,j)\) 这个点向上(其他方向同理)遇到的第一个坏的格子。显然这个格子也在第 \(j\) 列,所以只需要记录行的信息。初始时,\(f[i][j][0]=i\)(别忘了边界上向外一圈的点,它们可以用来当哨兵)。
当第 \((i,j)\) 个格子变好时,\(f[i][j][0]=i-1\),而如果 \((i-1,j)\) 此时也是好的,那么就继续往上,这里就类似于并查集寻找代表节点的方法,同时也可以加一个类似于路径压缩的优化。这样就可以在接近 \(O(1)\) 的时间里求出四个方向最远能到的点。
而对于新添加的好的子矩阵,显然需要包含新变好的格子。由上图中也可以发现,设 \(u[i]\) 表示第 \(i\) 列向上能到达对答案有贡献的格子数(向下同理),那么显然 \(i\) 在当前格子的左侧非严格单调递增,右侧非严格单调递减。
接下来就可以枚举新矩阵的左右边界,如下图所示
设当前矩阵的左右边界分别枚举到 \(i\) 和 \(j\)。那么当前矩阵的宽是固定的,也就不用考虑。而对于长,当前矩阵向上最远能到达的格子数即为 \(\min (ul_i,ur_j)\);同理,向下最远能到达的格子数即为 \(\min (dl_i,dr_j)\)。对答案的贡献也就是 \(\min (ul_i,ur_j)*\min (dl_i,dr_j)\),因为一定要经过当前新好的格子所在的列。
#include<cstdio>
using namespace std;
const int N=510;
#define int long long
int n,m,ans[N*N],f[N][N][4],dl[N],dr[N],ul[N],ur[N],X[N*N],Y[N*N]; //0上 1下 2左 3右
int find(int x,int y,int NLC)
{
if(NLC<=1) return f[x][y][NLC]==x?x:f[x][y][NLC]=find(f[x][y][NLC],y,NLC);
return f[x][y][NLC]==y?y:f[x][y][NLC]=find(x,f[x][y][NLC],NLC);
}
int min(int a,int b){return a<b?a:b;}
int max(int a,int b){return a>b?a:b;}
signed main()
{
scanf("%lld%lld",&n,&m);
for(int i=0;i<=n+1;i++)
for(int j=0;j<=m+1;j++)
f[i][j][0]=f[i][j][1]=i,f[i][j][2]=f[i][j][3]=j;
for(int i=n*m;i>=1;i--) scanf("%lld%lld",&X[i],&Y[i]);
for(int t=1;t<n*m;t++)
{
int x=X[t],y=Y[t];
f[x][y][0]=x-1,f[x][y][1]=x+1;
f[x][y][2]=y-1,f[x][y][3]=y+1;
int left=find(x,y,2),right=find(x,y,3),down=find(x,y,1),up=find(x,y,0);
ul[y]=ur[y]=x-up,dl[y]=dr[y]=down-x;
for(int i=y-1;i>left;i--)
{
ul[i]=min(x-find(x,i,0),ul[i+1]);
dl[i]=min(find(x,i,1)-x,dl[i+1]);
}
for(int i=y+1;i<right;i++)
{
ur[i]=min(x-find(x,i,0),ur[i-1]);
dr[i]=min(find(x,i,1)-x,dr[i-1]);
}
int res=0;
for(int y1=y;y1>left;y1--)
for(int y2=y;y2<right;y2++)
{
res+=min(ul[y1],ur[y2])*min(dl[y1],dr[y2]);
}
ans[t]=ans[t-1]+res;
}
for(int i=n*m-1;i>=0;i--) printf("%lld\n",ans[i]);
return 0;
}
义乌集训 2021.07.13 B
给定一个只包含小写字母、大写字母、数字的字符串串 \(s\) ,问其中有多少长度恰好为 \(6\) 的 \(namomo\) 子序列。 定义一个子序列 \(t\) 是 \(namomo\) 子序列,当且仅当
1.\(t[3]=t[5]\)
2.\(t[4]=t[6]\)
3.\(t[1],t[2],t[3],t[4]\) 两两不相同。
答案对 \(998244353\) 取模。
$6 \leq∣s∣\leq 10 $
首先可以想到枚举 \(t[3]\) 和 \(t[4]\),那么在枚举时再去算 \(t[1],t[2]\) 的方案显然就不现实了。于是就可以想到预处理出这些方案数。
设 \(f[i][j]\) 表示在字符串的前 \(i\) 个位置中,\(t[1],t[2]\) 不包含 \(s[i+1]\) 和 \(j\) 这两个字符的所有方案数。
可以想到用容斥原理,求出所有的方案(两个不相同),再减去包含 \(s[i+1]\) 和 \(j\) 的方案。
设 \(sum[i]\) 表示前 \(i\) 个位置的所有方案,\(num[i][j]\) 表示前 \(i\) 个字符中 \(j\) 出现的次数,那么 \(sum[i]=sum[i-1]+i-num[i][s[i]]\),同时因为 \(i\) 是往后枚举的,\(num\) 的第一维也就可以省去。
而对于不合法的方案,设 \(k1[i][j]\) 表示前 \(i\) 个字母中 \(t[1]=j\) 的所有方案,有 \(k1[i][j]=k1[i-1][j]+num[j]\),因为前面的所有 \(j\) 都可以和当前字母组合。
\(k2[i][j]\) 表示前 \(i\) 个字母中 \(t[2]=j\) 的所有方案。那么当 \(s[i]==j\) 时,\(k2[i][j]=k2[i-1][j]+i-num[j]\),因为当前的 \(j\) 可以和之前所有不是 \(j\) 的字符组合。当 \(s[i] \ne j\) 时,\(k2[i][j]=k2[i-1][j]\)。
但是显然这样还不够,因为多减去了 \(t[1],t[2]\) 都是 \(s[i+1]\) 和 \(j\) 的方案。设\(kk[i][j][k]\) 表示前 \(i\) 个字符中,第一个字符为 \(j\),第二个字符为 \(k\) 的所有方案。就有 \(kk[i][j][s[i]]=kk[i-1][j][s[i]]+num[j]\) 。
显然,\(k1,k2,kk\) 的第一维都可以用优化掉。
于是 \(f[i][j]=s[i]-((k1[s[i+1]]+k2[s[i+1]]+k1[j]+k2[j]-kk[s[i+1]][j]-kk[j][a[i+1]]))\)。
再考虑 \(t[3-6]\) 的取值。设 \(cnt[j][k]\) (这里就直接省略第一维了)表示 \(t[3]=j,t[4]=k\) 的所有方案。设 \(rc[j][k]\) 表示 \(t[5]=j,t[6]=k\) 的所有方案。显然 \(rc[j][k]+=suf[k]\),其中 \(suf[k]\) 表示 \([i,n]\) 中字符 \(k\) 的数量。同时也有 \(cnt[a[i]][j]+=rc[j][a[i]]\),这样枚举就是为了防止 \(t[3]\) 和 \(t[5]\) 重复。那么对于答案的贡献也就是:
\(if(s[i]!=j),ans+=cnt[j][s[i]]*f[i-1][j]\)。
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e6+10;
#define LL long long
const int mod=998244353;
const int S=62;
string str;
LL n,a[N],s[N],ans,f[N][S],t1[S],t2[S],t[S][S],num[S],cnt[S][S],rc[S][S],suf[S];
int main()
{
cin>>str;
n=str.length();
for(int i=0;i<n;i++)
{
if(str[i]>='0'&&str[i]<='9') a[i+1]=str[i]-'0';
if(str[i]>='a'&&str[i]<='z') a[i+1]=str[i]-'a'+10;
if(str[i]>='A'&&str[i]<='Z') a[i+1]=str[i]-'A'+36;
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<=61;j++)
{
if(a[i]!=j)
{
t1[j]+=num[j];
t[j][a[i]]+=num[j];
}
else t2[j]+=i-1-num[j];
}
num[a[i]]++;
s[i]=s[i-1]+i-num[a[i]];
for(int j=0;j<=61;j++)
{
if(a[i+1]!=j) f[i][j]=(s[i]-(t1[a[i+1]]+t2[a[i+1]]+t1[j]+t2[j]-t[a[i+1]][j]-t[j][a[i+1]]))%mod;
// if(f[i][j]>0) printf("%lld ",f[i][j]);
}
// puts("");
}
for(int i=n;i>=1;i--)
{
for(int j=0;j<=61;j++)
if(a[i]!=j) ans+=cnt[j][a[i]]%mod*f[i-1][j]%mod;
for(int j=0;j<=61;j++)
if(a[i]!=j) cnt[a[i]][j]+=rc[j][a[i]];
for(int j=0;j<=61;j++)
if(a[i]!=j) rc[a[i]][j]+=suf[j];
suf[a[i]]++;
}
printf("%lld\n",ans%mod);
return 0;
}
义乌集训 2021.07.13 C
给定一棵大小为 \(n\) 的有根树。每个节点有个非负权值 \(w_i\),对于每个节点 \(x\),我们找到包含 \(x\) 的节点的平均值最大的连通块,定义 \(f(x)\) 为这个平均值。请求出 \(\min f_i (i \in(1,2,3 \dots n))\)。
\(1 \leq n \leq 1e5\),\(0 <w_i \leq 1e9\)。
显然,本题要求的是最小值的最大值,即当所有联通块的取值最优时,最小值最大。显然可以二分答案。
判断当前的 \(mid\) 是否合法,也就是判断 \(\min f_i\) 与 \(mid\) 的大小关系。也就是 \(\dfrac{\sum w_i}{\sum 1} \geq mid\) 是否成立,也就是判断 \(\sum w_i-mid \geq 0\) 是否成立。那么就可以令 \(w_i=w_i-mid\),再让每个点按照最优方案联通,判断是否存在 \(f_i < 0\),如果不存在则合法。
关于最优联通方案,就可以用到换根 dp,具体来说,第一次扫描时,\(f[i]\) 的含义是在 \(i\) 的子树内包含 \(i\) 这个节点的连通块的最大值,易得状态转移方程为:
\(f[i]+=\max(f_j,0)(j \in son(i))\)。\(f[i]\) 的初值为 \(w[i]\)。
而对于第二次扫描,\(f[i]\) 的含义就是包含 \(i\) 的平均值最大的连通块的值。相比于第一次扫描,第二次扫描主要就是将除了 \(i\) 所在子树外其他点考虑进去了。那么 \(f[j]=\max(f[j],f[i]-max(f[j],0)+f[j])(j \in son(i))\)。主要就是对 \(f[j]\) 本来是否在 \(i\) 的最优决策中讨论。
最后判断是否存在 \(f[i] < 0\) 即可。同时需要注意精度问题。
#include<cstdio>
#include<iostream>
using namespace std;
const double eps=1e-7;
const int N=1e5+10;
int n,w[N],h[N],idx;
struct edge{
int v,nex;
}e[N];
double v[N],f[N];
void add(int u,int v)
{
e[++idx].v=v;
e[idx].nex=h[u];
h[u]=idx;
}
void dp1(int u)
{
f[u]=v[u];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
dp1(v);
f[u]+=max(f[v],0.0);
}
}
void dp2(int u)
{
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
f[v]=max(f[v],f[u]-max(0.0,f[v])+f[v]);
dp2(v);
}
}
bool check(double mid)
{
for(int i=1;i<=n;i++) v[i]=w[i]*1.0-mid;
dp1(1);
dp2(1);
for(int i=1;i<=n;i++)
if(f[i]<=-eps) return false;
return true;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
for(int u,v=2;v<=n;v++) scanf("%d",&u),add(u,v);
double l=0.0,r=10000000000.0;
while(r-l>eps)
{
double mid=(l+r)/2.0;
if(check(mid)) l=mid;
else r=mid;
}
printf("%lf\n",r);
return 0;
}
义乌集训 2021.07.14 C
对于 \([1,n]\) 的子集 \(A\),它的分数 \(s\) 为
1.初始分数为 \(0\);
2.对于所有的 \(i \in A,s+=a_i\);
3.对于所有满足 \(i,j \in{A \cap \geq 2}\),存在大于 \(2\) 的整数 \(k\) 使得,\(i^k=j\),\(s-=b_j\)。
求分数最高的子集的分数。
对于 \(20 \%\) 的数据,\(1 \leq n \leq20\)。
对于 \(100 \%\) 的数据,\(1 \leq n \leq 10^5,1 \leq a_i,b_i \leq 10^9\)。
考虑枚举每一个不能表示为 \(p^k\) 的数 \(x\),那么显然 \(x,x^2,x^3,\dots x^n\) 相互影响,但是它们的 \(b_i\) 不会影响其他的任何数。而即使 \(x=2\),最多也只有不超过 \(20\) 个数,也就可以直接 \(O(2^k)\) 枚举所有的选择方法,取最大值,最后再直接相加即可。因为越往后枚举,总的数的个数越来越少。
而对于 \(x \geq \sqrt{n}\),选择它们不会出现 \(-b_j\) 的情况。于是直接加进去即可。
#include<cstdio>
#include<cmath>
#include<vector>
using namespace std;
const int N=1e5+10;
#define int long long
const int INF=1e18;
int sum,ans,n,a[N],b[N],t[N],cnt;
bool vis[N],NLC[N];
vector<int> v[N];
int max(int a,int b){return a>b?a:b;}
void dfs(int now)
{
if(now>cnt)
{
int res=0;
for(int i=1;i<=cnt;i++)
{
if(!NLC[t[i]]) continue;
res+=a[t[i]];
for(int j=0;j<v[t[i]].size();j++)
{
if(NLC[v[t[i]][j]]) res-=b[t[i]];
}
}
sum=max(sum,res);
return ;
}
NLC[t[now]]=true;
dfs(now+1);
NLC[t[now]]=false;
dfs(now+1);
}
signed main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<=n;i++) scanf("%lld",&b[i]);
for(int i=2;i*i<=n;i++)
for(int j=i*i;j<=n;j*=i)
v[j].push_back(i);
for(int i=2;i*i<=n;i++)
{
if(vis[i]) continue;
cnt=0ll;
for(int j=i;j<=n;j*=i) vis[j]=true,t[++cnt]=j;
sum=-INF;
dfs(1);
ans+=sum;
}
for(int i=1;i<=n;i++)
{
if(!vis[i])
{
ans+=a[i];
}
}
printf("%lld\n",ans);
return 0;
}
义乌集训 2021.07.15 C
白云有一颗 \(n\) 个节点的树,每个点有一个点权
白兔需要找到两条点不相交的路径,要求最大化这两条路径覆盖点的点权和。
\(1 \leq n \leq 10^5\)
本题有一个显然的结论,这两条路径的选法只有两种:
1.是选一条直径,再在剩下的森林里选一条直径;
2.在直径上挂两条链,如下图所示。红色部分是直径,蓝色部分是选择的路径。
根据直径的最长性,这两条路径的端点显然至少有一个要在直径的两端上,也就有了上面的这两种情况。
情况 1 的做法和巡逻这道题一样,就不再赘述。
而第二种情况,设 \(i\) 表示直径上的第 \(i\) 个点,直径上一共有 \(s\) 个点,\(dis[i]\) 表示 \(i\) 到直径上第一个节点的路径长度,\(f[i]\) 表示该点向直径外走最远能到达的距离,那么答案就是 \(\max (dis[i]-w[i]+f[i]+dis[n]-dis[j]+f[j])(i \leq j)\)。
直接枚举的时间复杂度是 \(O(n^2)\) 的,但是可以发现,\(dis[i]-w[i]+f[i]+dis[n]\) 可以直接预处理出最大值,于是就可以 \(O(n)\) 求出第二种情况的最大值。
最后输出两种方案的最大值即可。
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int N=1e5+10;
const int M=2e5+10;
#define LL long long
vector<int> path;
const LL INF=1e18;
LL dis[N],w[N],ans,up[N],d1[N],d2[N],f[N],res,ans1,ans2;
int n,h[N],pre[N],idx=1,d,dr,son[N];
bool vis[N];
int max(int a,int b){return a>b?a:b;}
struct edge{
int v,nex;
bool broken;
}e[M];
void add(int u,int v)
{
e[++idx].v=v;
e[idx].nex=h[u];
h[u]=idx;
}
void dfs1(int u,int fa)
{
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa||vis[v]) continue;
dis[v]=dis[u]+w[v];
dfs1(v,u);
}
}
void dfs2(int u,int fa)
{
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa||vis[v]) continue;
if(dis[v]<dis[u]+w[v])
{
dis[v]=dis[u]+w[v];
pre[v]=i;
}
dfs2(v,u);
}
}
void dfs_nlc(int u,int fa)
{
d1[u]=w[u],d2[u]=-INF;
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(vis[v]||v==fa) continue;
dfs_nlc(v,u);
if(d1[v]+w[u]>d1[u]) d2[u]=d1[u],d1[u]=d1[v]+w[u],son[u]=v;
else if(d1[v]+w[u]>d2[u]) d2[u]=d1[v]+w[u];
}
}
void dfs_yy(int u,int fa)
{
res=max(res,up[u]+d1[u]);
vis[u]=true;
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(vis[v]||v==fa) continue;
if(son[u]==v) up[v]=d2[u];
else up[v]=d1[u];
dfs_yy(v,u);
}
}
void dfs_max(int u,int fa)
{
f[u]=w[u];
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa||vis[v]) continue;
dfs_max(v,u);
f[u]=max(f[u],f[v]+w[u]);
}
}
int main()
{
// freopen("attack1.in","r",stdin);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lld",&w[i]);
for(int u,v,i=1;i<n;i++) scanf("%d%d",&u,&v),add(u,v),add(v,u);
memset(dis,0,sizeof(dis));
dis[1]=w[1];
dfs1(1,0);
for(int i=1;i<=n;i++)
if(dis[i]>dis[d]) d=i;
memset(dis,0,sizeof(dis));
dis[d]=w[d];
dfs2(d,0);
dr=d;
for(int i=1;i<=n;i++)
if(dis[i]>dis[dr]) dr=i,ans=dis[i];
int now=dr;
while(now!=d)
{
vis[now]=true;
now=e[pre[now]^1].v;
}
vis[d]=true;
for(int i=1;i<=n;i++)
if(!vis[i])
{
dfs_nlc(i,0);
dfs_yy(i,0);
}
ans1=ans+res;
memset(vis,0,sizeof(vis));
now=dr;
while(now!=d)
{
path.push_back(now);
vis[now]=true;
now=e[pre[now]^1].v;
}
path.push_back(d);
reverse(path.begin(),path.end());
vis[d]=true;
for(int i=0;i<path.size();i++)
{
dfs_max(path[i],-1);
}
LL t=0;
for(int i=0;i<path.size();i++)
{
int u=path[i];
ans2=max(ans2,f[u]-dis[u]+t);
t=max(t,f[u]-w[u]+ans+dis[u]);
}
/* for(int i=0;i<path.size();i++)
for(int j=i+1;j<path.size();j++)
{
int u=path[i],v=path[j];
ans2=max(ans2,f[u]-w[u]+f[v]-w[v]+ans-(dis[v]-dis[u]));
}*/
printf("%lld\n",max(ans1,ans2));
return 0;
}
义乌集训 2021.07.15 D
白云在白兔的城市,打算在这里住 \(n\) 天,这 \(n\) 天,白云计划找白兔订购水。
白云给出了接下来的 \(n\) 天,每天的需水量,第 \(i\) 天为 \(D_i\) 升。
白兔给出了接下来的 \(n\) 天,每天水的价格,第 \(i\) 天为 \(P_i\) 元每升。
白云的小区有一个共用水壶,最大容量为 \(V\) 升,初始为空。 接下来每天,白云可以进行如下操作:
1.把水壶中的水使用掉
2.向白兔购买若干水,并放入水壶中
3.向白兔购买若干水,并使用(不一定全部使用完)
任何时候水壶中的水不能超过 \(V\) 升,而且每升水每在水壶中存放一天,需要付出 \(m\) 元
白兔为了难为白云,决定在某些天进行破坏操作,即选择一个子序列 \(b_1,\dots,b_t\)
,在这序列中的每一天,它会在当天早上把前一天储存的水放掉。第 \(i\) 天有一个破坏难度 \(val_i\),白兔为了挑战自己,决定让自己进行破坏操作的 \(val\) 是严格单调递增。它会找一个破坏天数最多的方案,在保证破坏次数最多的前提下,使得破坏序列的字典序最小。
对于破坏操作,显然就是求一个记录方案的最长上升子序列。\(O(n \log n)\) 时间求最长上升子序列以及方案可以自行百度。在此处为了保证字典序最小,就可以倒过来求一个最长下降子序列。
对于第 \(i\) 天买水的方案,设 \(j < i\),那么如果 \(p_j+(i-j)*m \leq p_i\),那么肯定就选择在第 \(j\) 天买水储存到第 \(i\) 天用。上面的不等式可以移项,也就是 \(p_j-j*m \leq p_i-m*i\),于是就可以维护一个 \(p_j-j*m\) 单调递增的序列。
这里有一个小技巧,将第 \(i\) 天插入队列时,先将 \(p_i\) 减去 \(m*i\),那么就相当于第 \(j\) 天在第 \(i\) 天的水价就是 \(p_j+m*j\)。
同时还需要注意一下水壶的容量上限 \(V\),这里其实可以理解为在第 \(i\) 天时穿越回第 \(j\) 天买水,此时的 \(V\) 就是买水上限,那么如果第 \(j\) 天剩余的水不够,那么就在这里买到上限,再到第 \(j'\) 天继续买。如果前面都不够,那就在今天买,由于这些水今天就会用掉,所以不会对容量造成影响。
同时如果在第 \(j\) 天买了 \(k\) 的水,那么对于之后的天内的容量就全部都会减少 \(k\),此时就可以对整个队列打上一个整体标记。第 \(i\) 天的容量减去整体标记 \(tag\) 才是真正可以买水的量。于是在 \(i\) 入队时,就直接将第 \(i\) 天的容量记为 \(V+tag\)。
最后注意,如果当天的水壶是要被破坏的,直接清空队列,因为不能再从前面买水了。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e6+10;
#define int long long
inline int read()
{
int s=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=s*10+ch-'0';
ch=getchar();
}
return s*f;
}
int f[N],len,n,pos[N],m,V,val[N],d[N],p[N],q[N],ans,tag,w[N];
bool broken[N];
signed main()
{
// freopen("new2.in","r",stdin);
// freopen(".out","w",stdout);
n=read(),m=read(),V=read();
for(int i=1;i<=n;i++) val[i]=read();
for(int i=1;i<=n;i++) d[i]=read();
for(int i=1;i<=n;i++) p[i]=read();
for(int i=n;i>=1;i--)
{
int l=1,r=len+1;
while(l<r)
{
int mid=l+r>>1;
if(val[i]>=f[mid]) r=mid;
else l=mid+1;
}
if(r==len+1) len++;
pos[i]=r;
f[l]=val[i];
}
int NLC=-999999999;
for(int i=1;i<=n&&len;i++)
{
if(pos[i]==len&&val[i]>NLC)
{
broken[i]=true;
len--;
NLC=val[i];
}
}
int hh=0,tt=-1;
int dt=0,dn=0;
for(int i=1;i<=n;i++)
{
if(broken[i]) hh=tt+1;
while(hh<=tt&&p[q[tt]]+dt>=p[i]) tt--;
int s=d[i];
while(hh<=tt)
{
if(s<w[q[hh]]-dn)
{
ans+=s*(p[q[hh]]+dt);
dn+=s;
s=0;
break;
}
else
{
ans+=(w[q[hh]]-dn)*(p[q[hh]]+dt);
s-=w[q[hh]]-dn;dn+=w[q[hh++]]-dn;
}
}
q[++tt]=i;
ans+=s*p[i];
w[i]=V+dn;p[i]-=dt;
dt+=m;
}
printf("%lld\n",ans);
return 0;
}
义乌集训 2021.07.16 C
白云有一个 \(1···n\) 的排列。白兔想从中选出一个大小为三的子序列。白云给了一个要求:这个子序列的第一个数必须是三个数中的最小值,第二个数必须是三个数中的最大值。白兔想知道它有多少种选子序列的方案。
对于 \(30\%\) 的数据,\(n \leq 100\);
对于 \(50\%\) 的数据,\(n \leq 1000\);
对于 \(80\%\) 的数据,\(n \leq 10^5\);
对于 \(100\%\) 的数据,\(n \leq 3×10^6\);
形式化来说,设 \(1\) 表示三个数中第一小,\(2\) 表示三个数中第二小的,\(3\) 表示三个数中最大的。题意就是需要求出所有的 \(1,3,2\) ,直接求比较困难。于是可以想到利用容斥原理,求出所有的 \(1,x,x\) ,再减去所有的 \(1,2,3\) 即可。
对于所有的 \(1,x,x\),设 \(k_i\) 表示在 \([i+1,n]\) 中有 \(k_i\) 个数比 \(p[i]\) 大,那么 \(tot=\sum_{i=1}^{n-2} C_{k_i}^{2}\)。
而对于所有的 \(1,2,3\) ,枚举 \(1\) 或 \(3\) 比较困难,于是可以直接枚举 \(2\),设 \(t_i\) 表示在 \([1,i-1]\) 中有 \(t_i\) 个数比 \(p[i]\) 小。那么 \(tot'=\sum_{i=2}^{n-1} t_i*p_i\)。
最终的 \(ans=tot-tot'\)。
而对于 \(k,t\) 数组,就可以开一个在值域上的树状数组。在 \(O(n \log n)\) 的时间内求出。
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<ctime>
using namespace std;
const int N=3e6+10;
unsigned long long seed;
unsigned long long rd()
{
seed ^= seed << 13;
seed ^= seed >> 7;
seed ^= seed << 17;
return seed;
}
#define int long long
int premin[N],nexmax[N],c[N],ans,n,p[N];
int lowbit(int x){return x&-x;}
void add(int x,int k){ while(x<=n) c[x]+=k,x+=lowbit(x);}
int query(int x){ int res=0;while(x) res+=c[x],x-=lowbit(x);return res;}
signed main()
{
// freopen("triple.in","r",stdin);
// freopen("triple.out","w",stdout);
cin>>n>>seed;
p[1]=1;
for(register int i=2;i<=n;i++)
{
p[i]=i;
swap(p[i],p[rd()%i+1]);
}
for(int i=1;i<=n;i++)
{
premin[i]=query(p[i]-1);
add(p[i],1);
}
memset(c,0,sizeof(c));
for(int i=n;i>=1;i--)
{
nexmax[i]=query(n)-query(p[i]);
add(p[i],1);
}
for(int i=1;i<=n;i++) ans+=nexmax[i]*(nexmax[i]-1)/2-premin[i]*nexmax[i];
printf("%lld\n",ans);
return 0;
}
义乌集训 2021.07.16 D
有一天 Mifafa 回到家,发现有 \(n\) 只老鼠在她公寓的走廊上,她大声呼叫,所以老鼠们都跑进了走廊的洞中。
这个走廊可以用一个数轴来表示,上面有 \(n\) 只老鼠和 \(m\) 个老鼠洞。第 \(i\) 只老鼠有一个坐标 \(x_i\),第 \(j\) 个洞有一个坐标 \(p_j\) 和容量 \(c_j\) 。容量表示最多能容纳的老鼠数量。
找到让老鼠们全部都进洞的方式,使得所有老鼠运动距离总和最小。
老鼠 \(i\) 进入洞 \(j\) 的运动距离为 \(|x_i-p_j|\) 。
无解输出 \(-1\)。
本题无解,当且仅当 $\sum_{i=1}^{m}c_i < m $。
首先可以想到按照 \(x_i\) 对老鼠进行排序,那么排序后的老鼠就一定会是一段老鼠进入同一个洞中,不存在两端进同一个洞,而中间去别的洞的情况。因为显然这样的运动距离更大。于是可以考虑反悔贪心。
首先将所有的老鼠和洞按照坐标排序。将所有有容量的洞存入一个小根堆中,比较关键字为 \(-p_j\),即第 \(i\) 只老鼠进入左边的洞的代价为 \(x_i-p_j\),此处只考虑老鼠左边的洞。
显然,第 \(i\) 只老鼠不只可能进入左边的第 \(j\) 个洞,也可能进入右边的第 \(k\) 个洞,即当 \(p_k-x_i <x_i-p_j\) 时,第 \(i\) 只老鼠进入它右边的洞更优。那么就可以将可能反悔的老鼠存入另一个小根堆中,比较关键字为 \(-(x_i+x_i-p_j)\),因为将老鼠放到第 \(k\) 个洞后减小的代价为 \(p_k-(x_i+x_i-p_j)\)。那么显然后面的越小越好。
当然,如果因为当前老鼠进入右边的洞,导致后面的老鼠 \(t\) 进不去了,那么此时显然要把这只老鼠赶回原来的洞,也就是洞也可以反悔。记老鼠进入右边的洞减小的代价为 \(w_i=p_k-(x_i+x_i-p_j)\),那么此时反悔减小的代价就是 \(p_t-x_k+w_i\),因为要把老鼠反悔减小的代价再重新加上,即将当前可能反悔的洞插入洞的小根堆中。
对于老鼠跑到右边的洞,其实不需要把原先左边的洞的容量加回来,因为按照上述的排序方式,在考虑后面的老鼠时,会优先考虑右边的洞,其次再考虑将这只老鼠反悔,最后再考虑左边的洞。所以在考虑当前洞的时候,实际上所有去右边洞的老鼠都已经回到当前洞了。
#include<queue>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=2e6+10;
#define int long long
const int INF=1e15;
struct node{
int w,id;
inline bool operator <(const node &b)const{
return w>b.w;
}
};
priority_queue<node>q1;//hole
priority_queue<int,vector<int>,greater<int> >q2;//mice
pair<int,int> q[N];
inline int read()
{
int s=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
s=s*10+ch-'0';
ch=getchar();
}
return s*f;
}
int n,m,ans;
signed main()
{
// while(1) puts("NLC AK IOI!!!!!!");
// freopen("data.in","r",stdin);
n=read(),m=read();
for(int i=1;i<=n;i++) q[i].first=read(),q[i].second=-1;
int NLC=0;
for(int i=1;i<=m;i++) n++,q[n].first=read(),q[n].second=read(),NLC+=q[n].second;
if(NLC<n-m)
{
puts("-1");
return 0;
}
sort(q+1,q+n+1);
for(int w,id,i=1;i<=n;i++)
{
if(q[i].second==-1)
{
w=INF;
if(q1.size())
{
id=q1.top().id;
w=q[i].first+q1.top().w;
q1.pop();
if(q[id].second) q[id].second--,q1.push(node{-q[id].first,id});
}
ans+=w;
q2.push(-w-q[i].first);
}
else
{
// printf("%lld\n",q2.top());
while(q[i].second&&q2.size()&&q2.top()+q[i].first<0)
{
w=q2.top()+q[i].first;
q2.pop();ans+=w;
q[i].second--;
q1.push(node{-w-q[i].first,0});
}
if(q[i].second) q1.push(node{-q[i].first,i}),q[i].second--;
}
}
printf("%lld\n",ans);
return 0;
}
义乌集训 2021.07.17 B
白云开着飞机带白兔来到了一座城市,这座城市有 \(n\) 个景点。
这座城市的道路非常有意思,每个景点都恰好存在一条通往其它某个节点的单向道路。
现在白云可以把飞机降落在任何一个景点,然后让白兔独自旅行。当白兔旅行结束时,白云会到白兔所在的景点来接它。而在旅行的中途,白兔只能靠城市的道路来移动。
现在白兔想制定一个旅游的顺序,按照这个顺序依次前往每一个景点。在每个景点游玩会消耗白兔一定的体力值。为了让白兔有充足的信心,我们的这个方案必须满足:每次游览景点所消耗的体力值必须 严格 比前一个景点消耗的体力值要小。
白兔想知道它最多能去几个景点游玩。
每个景点消耗的体力值在 \([0, 10^9 ]\) 范围内
对于 \(30\%\) 的数据,\(n \leq 1000\);
对于 \(50\%\) 的数据,\(n \leq 10000\);
对于 \(100\%\) 的数据,\(n \leq 100000\);
看到每个点有且仅有一条出边,那么显然本题就是一个内向基环树森林,对于这种特殊的图,显然最后会走到环上,但是由于起点不确定,就可以将原题意转化为从环上出发,求一个最长上升子序列的长度。
而题目中并没有说经过一个节点就一定要玩,也可以先经过这个节点去玩其他的节点再回过头来玩它。那么在环上的最优游览路径就是游览全部的(体力值一样的节点除外)节点,再往子树内走,往哪棵子树走其实都可以。那么就可以对于每一个子树以及环,求一次最长上升子序列(就是 \(O(n \log n)\) 做法在树上的推广)。最后再取最大值即可。
由于除了基环树上的点都会被求一次最长上升子序列,所以最终的时间复杂度还是 \(O(n \log n)\)。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2e5+10;
int rh[N],h[N],idx,cir[N],n,val[N],fa[N],cnt,en[N],ans,f[N],len,tlen,tot,din[N];
bool ins[N],nlc[N];
struct edge{
int v,nex;
}e[N<<1];
bool vis[N];
void add(int h[],int u,int v)
{
e[++idx].v=v;
e[idx].nex=h[u];
h[u]=idx;
}
void dfs_cir(int u)
{
nlc[u]=ins[u]=true;
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
fa[v]=u;
if(!nlc[v]) dfs_cir(v);
else if(ins[v])
{
int k=u;
cnt++;
en[cnt]=en[cnt-1];
while(k!=v)
{
vis[k]=true;
cir[++en[cnt]]=k;
k=fa[k];
}
vis[v]=true;
cir[++en[cnt]]=v;
}
}
ins[u]=false;
}
void dfs(int u)
{
if(len==0) printf("%d %d ",len,u);
for(int i=rh[u];i;i=e[i].nex)
{
int v=e[i].v;
if(vis[v]) continue;
if(val[v]>f[len])
{
f[++len]=val[v];
ans=max(ans,len);
dfs(v);
f[len--]=0;
}
else
{
int p=lower_bound(f+1,f+len+1,val[v])-f;
int t=f[p];
f[p]=val[v];
dfs(v);
f[p]=t;
}
}
}
int main()
{
// freopen("travel1.in","r",stdin);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&val[i]);
for(int v,u=1;u<=n;u++) scanf("%d",&v),add(h,u,v),add(rh,v,u);
for(int i=1;i<=n;i++) if(!nlc[i]) dfs_cir(i);
for(int i=1;i<=cnt;i++)
{
len=0;
for(int j=en[i-1]+1;j<=en[i];j++) f[++len]=val[cir[j]];
sort(f+1,f+len+1);
ans=max(ans,len);
for(int j=en[i-1]+1;j<=en[i];j++) dfs(cir[j]);
}
printf("%d\n",ans);
return 0;
}
义乌集训 2021.07.17 C
白兔有一棵 \(n\) 个结点带边权的树。定义 \(g(x, y)\) 为 \(x\) 和 \(y\) 两个点路径上所有边权最大值。特别地,\(g(x, x) = 0\)。
白云想构造一个序列 \(p_1 · · · p_n\),一个序列的价值为 \(min^{n} _{i=1} g(i, p_i)\) 。同时,白兔给了白云一个限制:任何一个数 \(x\) 在序列中不得超过 \(s_x\) 次。
白云想知道满足要求的所有序列的最大价值。
对于 \(30\%\) 的数据,\(n \leq 10\);
对于 \(60\%\) 的数据,\(n \leq 1000\);
对于 \(100\%\) 的数据,\(n \leq 10^5,w \leq 10^9,1 \leq s_i \leq n≤10^5\)
看到最小值的最大值,显然就可以二分答案。
首先将边按照边权大小排序,将所有边权小于 \(mid\) 所连接的边缩点,缩成一个节点后,显然这些节点的 \(p_i\) 是在外部。
那么对于缩点之后的树,只要判断是否存在 \(size_i >\sum_{j \ne i} s_j\)。其中 \(size_i\) 表示缩点后第 \(i\) 个点内点的数量,\(sum_i\) 表示该点内所有点的 \(s_i\) 之和。如果存在,就说明这些点注定有一部分点的 \(g\) 无法大于等于 \(mid\)。 那么就需要减小 \(mid\),反之则增大。
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10;
struct edge{
int u,v,w;
bool operator <(const edge &t)const{
return w<t.w;
}
}e[N];
int f[N],n,tot,s[N],sum[N];
int siz[N];
void swap(int &a,int &b){int t=a;a=b,b=t;}
int find(int x){return f[x]==x?x:f[x]=find(f[x]);}
bool check(int mid)
{
memset(siz,0,sizeof(siz));
memset(sum,0,sizeof(sum));
int now=1;
for(int i=1;i<=n;i++) f[i]=i,sum[i]=s[i],siz[i]=1;
while(e[now].w<mid&&now<n)
{
int fx=find(e[now].u),fy=find(e[now].v);
if(fx!=fy)
{
// if(siz[fx]<siz[fy]) swap(fx,fy);
f[fy]=fx;
siz[fx]+=siz[fy];
sum[fx]+=sum[fy];
}
now++;
}
for(int i=1;i<=n;i++)
{
int fx=find(i);
if(siz[fx]>tot-sum[fx]) return false;
}
return true;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<n;i++) scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
sort(e+1,e+n);
for(int i=1;i<=n;i++) scanf("%d",&s[i]),tot+=s[i];
int l=0,r=1e9;
while(l<r)
{
int mid=l+r+1>>1;
if(check(mid)) l=mid;
else r=mid-1;
}
printf("%d\n",r);
return 0;
}
义乌集训 2021.07.18 C
白云和白兔想占领一棵树。
白云列举了游戏玩法:
首先,白云任意选择一个结点 \(k\),把这个结点占领,其它结点都未被占领。
每一轮,白云可以选择若干个已经被占领的点,然后分别从每个点出发,找一条出边,把到达的结点占领。
当所有结点都被占领时游戏结束。
白兔想知道,选择一个最优的 \(k\),白云最少几轮可以完成游戏。
接下来白云和白兔想一起玩游戏,规则是这样:
一开始,白云选择了 \(a\) 号点,白兔选择了 \(b\) 号点,这两个结点都被占领,其它点都未被占领。
每一轮,白兔可以选择若干个已经被占领的点,然后分别从每个点出发,找任意一条出边,把到达的结点占领。
白兔还想知道,最小多少轮可以占领所有结点?注意,这个游戏的 \(a\) 和 \(b\) 是固定的。
对于 \(100\%\) 的数据,\(n \leq 10^5, a, b \in [1, n], a \ne b\)。
对于第一问,显然是一个换根 dp。
首先以 \(a\) 节点为根(做第二问时要用到),向下扫描一遍,得到 \(g_i\),表示以 \(i\) 为起点占领整棵子树所需要的最小轮数。设 \(j\) 表示 \(i\) 的第 \(j\) 个儿子,那么 \(g_i=\max(g_j+j)\)。
但是这样显然不是最优的,而优先占领 \(g_j\) 大的子树才是最优的。那么就可以将子树先排序一遍,再取最大值。
第二次扫描得到 \(f_i\),即以 \(i\) 的父亲为根,占领除了 \(i\) 所在的子树的其他所有部分所需要的时间。那么就将 \(i\) 的所有子树和 \(i\) 的父亲放入数组中按照 \(g_i\) 排序(父亲是 \(f_i\))。
对于求出 \(f[j]\),显然占领比 \(g_j\) 大的子树的时间显然不变,(除了子树 \(i\) 以外的其他部分也可能在这里) 而对于占领比 \(g_j\) 小的子树,因为不需要占领 \(j\)了,所以时间会在原来的基础上减少 \(1\)。
于是可以预处理出 \(pre\) 数组表示前面 \(g_i+i\) 的最大值,以及 \(suf\) 数组表示后面 \(g_i+i\) 的最大值。那么此时以 \(i\) 为根的答案就是 \(ans=min(ans,suf[0])\)(也可以是\(pre[k]\))。而 \(f[j]=max(pre[i-1],suf[i+1]-1)\)。
对于第二问,显然存在一条边,使得这条边的一侧全部被 \(a\) 占领,另一侧全部被 \(b\)占领。
而这条边显然就是在 \(a \to b\) 的链上(这里就解释为什么第一问要以 \(a\) 为根,因为此时 \(b\) 一直往父亲条就是 \(b \to a\) 的路径)。
于是就可以二分枚举这条边。将这条边删去,对于 \(a,b\) 做一次树形 dp。在此处显然 \(g[a]\) 和 \(g[b]\) 都具有单调性,且是相反的。而 \(ans=min(max(g[a],g[b]))\)。在两个函数的交点显然最优。这也是为什么本问可以用二分。
#include<cstdio>
#include<algorithm>
#include<vector>
#include<iostream>
using namespace std;
const int N=3e5+10;
const int INF=0x3f3f3f3f;
vector<int>e[N];
int ans,n,fa[N],a,b,g[N],f[N];
int pre[N],suf[N];
void add(int u,int v){e[u].push_back(v);e[v].push_back(u);}
void del(int u,int v){e[u].erase(find(e[u].begin(),e[u].end(),v)),e[v].erase(find(e[v].begin(),e[v].end(),u));}
void dfs_nlc(int u)
{
vector<int> val;
for(int i=0;i<e[u].size();i++)
{
int v=e[u][i];
if(v!=fa[u]) fa[v]=u,dfs_nlc(v),val.push_back(g[v]);
}
sort(val.begin(),val.end(),greater<int>());
if(val.size()) g[u]=0;
for(int i=0;i<val.size();i++)
{
// printf("NLC%d ",val[i]);
g[u]=max(g[u],val[i]+i+1);
}
// if(val.size()) puts("");
// printf("%d %d\n",e[u].size(),g[u]);
}
void dfs_yy(int u)
{
vector<pair<int,int> >val;
for(int i=0;i<e[u].size();i++) {int v=e[u][i];if(v!=fa[u]) val.push_back(make_pair(g[v],v));}
if(fa[u]) val.push_back(make_pair(f[u],u));
sort(val.begin(),val.end(),greater<pair<int,int> >());
pre[0]=val[0].first+1;suf[val.size()]=0;
for(int i=1;i<val.size();i++){pre[i]=max(pre[i-1],val[i].first+i+1);}
for(int i=val.size()-1;i>=0;i--){suf[i]=max(suf[i+1],val[i].first+i+1);}
// printf("%d\n",suf[0]);
ans=min(ans,suf[0]);
for(int i=0;i<val.size();i++)
{
int v=val[i].second;if(v==u) continue;
if(i>0) f[v]=max(pre[i-1],suf[i+1]-1);
else f[v]=suf[i+1]-1;
// printf("%d\n",f[v]);
}
for(int i=0;i<e[u].size();i++)
if(e[u][i]!=fa[u]) dfs_yy(e[u][i]);
}
void solve1()
{
ans=INF;
dfs_nlc(a);dfs_yy(a);//以x为根可以方便solve2
printf("%d\n",ans);
}
void solve2()
{
vector<int> v;
int y=b;
while(y) v.push_back(y),y=fa[y];
fa[b]=0;
int l=0,r=v.size()-2;ans=INF;
while(l<=r)
{
int mid=l+r>>1,ansx,ansy;
del(v[mid],v[mid+1]);
dfs_nlc(a),ansx=g[a];
dfs_nlc(b),ansy=g[b];
ans=min(ans,max(ansx,ansy));
add(v[mid],v[mid+1]);
if(ansx>ansy) l=mid+1;
else r=mid-1;
}
printf("%d\n",ans);
}
int main()
{
// freopen("game1.in","r",stdin);
scanf("%d%d%d",&n,&a,&b);
for(int u,v,i=1;i<n;i++) scanf("%d%d",&u,&v),add(u,v);
// printf("%d\n",n);
solve1();
solve2();
return 0;
}
义乌集训 2021.07.19 D
题意同[JSOI2018]潜入行动。
给定一棵 \(n\) 个点的树,要求在上面放置恰好 \(k\) 个装置,使得每个点的相邻节点(不包含自身)至少有一个装置,每个点只能安装至多一个装置,求方案数,对\(1000000007\) 取模。
对于 \(30\%\) 的数据,\(n \leq 100\)
对于另外 \(30\%\) 的数据,\(k \leq 20\)
对于另外 \(20\%\) 的数据,输入的树是一条链
对于 \(100\%\) 的数据,\(n \leq 100000,k \leq \min(n,200)\)
本题显然是一个树形dp。
设 \(f[i][j][k][t]\) 表示在子树 \(i\) 中放置了 \(j\) 个装置,且 \(i\) 是否放置了装置(\(k=1/0\)),且 \(i\) 是否被它的儿子看到\((t=1/0)\) 的方案数。
这里之所以 \(t=0\) 会存在,是因为它还有可能被父亲看到,在转移时注意一下即可。
初始时,\(f[u][0][0][0]=f[u][1][1][0]=1\)。
显然需要分四类讨论。
1.\(f[u][j+k][0][1]\),表示 \(u\) 没放装置,被儿子看到。
如果在考虑 \(v\) 这棵子树之前就已经被儿子看到,那么 \(v\) 就不一定要放装置,但一定要被它的儿子看到,因为 \(u\) 没放装置,看不了 \(v\)。而如果之前还没被看到,那么 \(v\) 就一定要放置装置,同时也要被它的儿子看到。即:
\(f[u][j+k][0][1]+=f[u][j][0][1]*(f[v][k][0][1],f[v][k][1][1])+f[u][j][0][0]*f[v][k][1][1]\)。
2.\(f[u][j+k][0][0]\),表示 \(u\) 没放装置,也没被儿子看到。
在考虑 \(v\) 之前也一定没有被看到,且此时 \(v\) 也没有放置装置,但一定要被看到。
\(f[u][j+k][0][0]+=f[u][j][0][0]+f[v][k][0][1]\)。
3.\(f[u][j+k][1][0]\),表示 \(u\) 放装置,但没被儿子看到。
在考虑 \(v\) 这棵子树前,\(u\) 显然已经被放了装置,但因为它没被看到,所以 \(v\) 不能放装置,是否被它的儿子看到无所谓,因为它都会被 \(u\) 看到。
\(f[u][j+k][1][0]+=f[u][j][1][0]*(f[v][k][0][0]+f[v][k][0][1])\)。
4.\(f[u][j+k][1][1]\),表示 \(u\) 放装置,也被儿子看到。
在考虑 \(v\) 这棵子树前,如果 \(u\) 已经被看到,那么此时无论 \(v\) 的状态是什么都满足题意。而如果 \(u\) 没被看到,那么此时 \(v\) 就要放置装置,但是不需要一定被儿子看到。
\(f[u][j+k][1][1]+=f[u][j][1][1]*(f[v][k][1][1]+f[v][k][1][0]+f[v][k][0][1]+f[v][k][0][0])+f[u][j][1][0]*(f[v][k][1][1]+f[v][k][1][0])\)。
最终的答案就是 \(f[1][k][0][1]+f[1][k][1][1]\)。
这样看上去复杂度是 \(O(n^3)\) 的,事实上,如果加了只枚举到 \(siz[u]\) 和 \(siz[v]\) 的优化,时间复杂度就会降到 \(O(n^2)\)。同时需要注意,本题中如果直接取模会极大降低运行效率,所以需要手动取模。
#include<cstdio>
using namespace std;
const int N=1e5+10;
const int M=210;
long long mod=1e9+7;
int f[N][M][2][2],n,K,idx,h[N],siz[N],tmp[M][2][2];
struct edge{
int v,nex;
}e[N<<1];
inline int min(int a,int b){return a<b?a:b;}
inline void add(int u,int v){e[++idx].v=v;e[idx].nex=h[u];h[u]=idx;}
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
inline int NLC(int a,long long b)
{
if(b>=mod) b%=mod;
a+=b;
while(a>=mod) a-=mod;
return a;
}
void dfs(int u,int fa)
{
// printf("%d\n",u);
siz[u]=f[u][0][0][0]=f[u][1][1][0]=1;
for(register int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(v==fa) continue;
dfs(v,u);
// printf("%d %d\n",u,v);
for(register int j=0;j<=min(siz[u],K);j++) tmp[j][0][0]=f[u][j][0][0],f[u][j][0][0]=0,tmp[j][1][0]=f[u][j][1][0],f[u][j][1][0]=0,tmp[j][0][1]=f[u][j][0][1],f[u][j][0][1]=0,tmp[j][1][1]=f[u][j][1][1],f[u][j][1][1]=0;
for(register int j=0;j<=min(siz[u],K);j++)
for(register int k=0;k<=min(siz[v],K-j);k++)
{
f[u][j+k][1][0]=NLC(f[u][j+k][1][0],1ll*tmp[j][1][0]*(f[v][k][0][1]+f[v][k][0][0]));//放了,但是没有被监听
f[u][j+k][0][1]=NLC(f[u][j+k][0][1],1ll*tmp[j][0][1]*(f[v][k][0][1]+f[v][k][1][1])+1ll*tmp[j][0][0]*f[v][k][1][1]);//没放,但是被监听了
f[u][j+k][1][1]=NLC(f[u][j+k][1][1],1ll*tmp[j][1][0]*(f[v][k][1][0]+f[v][k][1][1])+1ll*tmp[j][1][1]*(1ll*f[v][k][0][0]+1ll*f[v][k][0][1]+1ll*f[v][k][1][0]+1ll*f[v][k][1][1])%mod);
f[u][j+k][0][0]=NLC(f[u][j+k][0][0],1ll*tmp[j][0][0]*f[v][k][0][1]);
}
siz[u]+=siz[v];
}
}
int main()
{
scanf("%d%d",&n,&K);
for(register int u,v,i=1;i<n;i++) u=read(),v=read(),add(u,v),add(v,u);
dfs(1,0);
printf("%d\n",(f[1][K][0][1]+f[1][K][1][1])%mod);
return 0;
}
义乌集训 2020.07.20 A
小a有一个数列 \(a\),记 \(f(x)\) 表示斐波那契数列第 \(x\) 项,其中 \(f(1)=f(2)=1\)。
若干次操作,\(1\) 表示对数列 \(a\) 区间加,\(2\) 表示求 \(\sum f(a_i)\),其中 \(i\) 在\(l\) 到 \(r\) 之间。
由于 \(2\) 的答案可能非常大,所以对 \(10^9+7\) 取模。
对于 \(30\%\) 的数据,\(n \le 10^3\)。
对于 \(60\%\) 的数据,\(n \le 10^4\) 。
对于 \(100\%\) 的数据,\(n \le10^5\)。
对于这么大的斐波那契数列,显然直接递推是不行的,于是就要用到矩阵快速幂。由于每次的乘法都是乘以转移矩阵的 \(2^i\) ,于是可以先预处理出来这部分内容。
而对于区间加操作,这里可以直接将 \(tag\) 定义为转移矩阵的若干次幂。其他的地方就和一般的线段树没有较大差别了。
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e5+10;
const int mod=1e9+7;
struct node{
int a[2][2];
node operator +(const node &t)const{
node c;
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
c.a[i][j]=(a[i][j]+t.a[i][j])%mod;
return c;
}
node operator *(const node &t)const{
node c;
memset(c.a,0,sizeof(c.a));
for(int i=0;i<2;i++)
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
c.a[i][j]=(1ll*c.a[i][j]+1ll*a[i][k]*t.a[k][j])%mod;
return c;
}
}pow[40],tmp;
struct tree{
int l,r,mid;
bool flag;
node val,tag;
}tr[N<<2];
int n,m,a[N];
void init()
{
pow[0].a[1][1]=pow[0].a[0][1]=pow[0].a[1][0]=1;
pow[0].a[0][0]=0;
for(int i=1;i<=30;i++) pow[i]=pow[i-1]*pow[i-1];
}
node power(int k)
{
node res;
res.a[0][0]=res.a[1][1]=1;
res.a[0][1]=res.a[1][0]=0;
for(int i=0;k>0;i++,k>>=1)
if(k&1) res=res*pow[i];
return res;
}
void push_up(int p){tr[p].val=tr[p<<1].val+tr[p<<1|1].val;}
void push_down(int p)
{
if(tr[p].flag)
{
tr[p<<1].flag=tr[p<<1|1].flag=true;
tr[p<<1].tag=tr[p<<1].tag*tr[p].tag;
tr[p<<1|1].tag=tr[p<<1|1].tag*tr[p].tag;
tr[p<<1].val=tr[p<<1].val*tr[p].tag;
tr[p<<1|1].val=tr[p<<1|1].val*tr[p].tag;
tr[p].flag=false;
tr[p].tag=power(0);
}
}
void build_tree(int p,int l,int r)
{
tr[p].l=l,tr[p].r=r,tr[p].mid=(l+r)>>1,tr[p].flag=false,tr[p].tag=power(0);
if(l==r)
{
tr[p].val=power(a[l]);
return ;
}
build_tree(p<<1,tr[p].l,tr[p].mid);
build_tree(p<<1|1,tr[p].mid+1,tr[p].r);
push_up(p);
}
void updata(int p,int l,int r)
{
if(l<=tr[p].l&&tr[p].r<=r)
{
tr[p].flag=true;
tr[p].val=tr[p].val*tmp;
tr[p].tag=tr[p].tag*tmp;
return ;
}
push_down(p);
if(l<=tr[p].mid) updata(p<<1,l,r);
if(r>tr[p].mid) updata(p<<1|1,l,r);
push_up(p);
}
node query(int p,int l,int r)
{
if(l<=tr[p].l&&tr[p].r<=r) return tr[p].val;
push_down(p);
node res;
res.a[0][0]=res.a[1][0]=res.a[0][1]=res.a[1][1]=0;
if(l<=tr[p].mid) res=res+query(p<<1,l,r);
if(r>tr[p].mid) res=res+query(p<<1|1,l,r);
return res;
}
int main()
{
init();
// for(int i=1;i<=5;i++) printf("%d\n",power(i).a[0][0]);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
build_tree(1,1,n);
for(int i=1;i<=m;i++)
{
int opt,l,r,x;
scanf("%d%d%d",&opt,&l,&r);
if(opt==1)
{
scanf("%d",&x);
tmp=power(x);
updata(1,l,r);
} else printf("%d\n",query(1,l,r).a[0][1]);
}
return 0;
}
义乌集训 2021.07.20 B
小a有三种颜色的珠子,分别有 \(x,y,z\) 个,保证 \(x+y+z\) 一定是某个高度为 \(n\) 的金字塔,即第 \(i\) 行有恰好 \(i\) 个珠子,并且小 \(a\) 希望每一行的珠子颜色相同,现在小a想问你对于给定的 \(x,y,z\),是否存在这样一组解。
对于 \(30\%\) 的数据,\(x+y+z \le 300\)。
对于 \(60\%\) 的数据,\(x+y+z\le10^5\) 。
对于 \(100\%\) 的数据,\(x+y+z \le2\times10^9\)。
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
const int N=510;
const int M=4e5+10;
int T,x,y,z,f[N][M],s[N],n;
void swap(int &a,int &b){int t=a;a=b,b=t;}
int min(int a,int b){return a>b?a:b;}
bool ok;
void dfs(int now,int a,int b,int c)
{
if(a>x||b>y||c>z||ok==true) return ;
if(now<1)
{
ok=true;
return ;
}
dfs(now-1,a+now,b,c);
dfs(now-1,a,b+now,c);
dfs(now-1,a,b,c+now);
}
int main()
{
// freopen("b.in","r",stdin);
// freopen("b.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d%d%d",&x,&y,&z);
long long k=x+y+z;
n=(sqrt(1ll+8ll*(k))-1ll)/2ll;
if(x<y) swap(x,y);
if(y<z) swap(y,z);
if(x<y) swap(x,y);
if(x==x+y+z)
{
puts("1");
continue;
}
ok=false;
dfs(n,0,0,0);
printf("%d\n",ok);
}
return 0;
}