(同时也是HDU 2982,UVA的数据多)
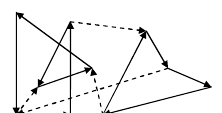
题意:平面上有m条有向线段连接了n个点。你从某个点出发顺着有向线段行走,给走过的每条线段涂一种不同的颜色,最后回到起点。你可以多次行走,给多个回路涂色(要么不涂色,要么就至少给一个回路上的边全部涂色)。可以重复经过一个点,但不能重复经过一条有向线段。如下图所示的是一种涂色方法(虚线表示未涂色,即每次都可以从任意点出发染色)。每涂一个单位长度将得到X分,但每使用一种颜色将扣掉Y分。假设你拥有无限多种的颜色,问如何涂色才能使得分最大?输入保证若存在有向线段u -> v,则不会出现有向线段v -> u。
n <= 100,m <= 500,1 <= X,Y <= 1000。
对于坐标(x,y)0 <= x,y <= 1000。
思路:看刘汝佳的书的第二种方法,再参考这篇博文才把代码长度降下来了。http://blog.csdn.net/u013368721/article/details/30553815
要求的就是最大费用循环流(即每找到一个环就可以进行增广)。找环可能并不复杂,但是要找一个最大的环就有点复杂了,所以用网络流解决。又因为找的是最大费用,按老套路的话会出现无限增大费用的情况,所以要先将每条边的费用取相反数(前面加个负),才可以有机会求最小费用流。而这些边的权有正有负,取完之后也可能出现负环了,所以主要问题就是解决负环。
用最小费用流求最大费用循环流时,解决负环的一种方法:
(1)先将所有边权取反。
(2)建边。正权值的边容量为1,费用为权值。负权值的边u->v拆成3条边,分别是S->v,v->u,u->T,容量都为1,v->u费用为负权的相反数,其他2条费用为0。这样会出现某个点有多条边连到S或T,可以互相抵消到一方为0为止,统计剩下多少条k,将其中1条的容量设为k,其他的全部删掉。如果全部抵消掉了,那就将连S和T的边全部删掉。(这个删边的方法有技巧)
(3)跑一次最小费用流得到的总费用,加上所有负权之和之后(注:此时答案已为负的),再取反即得到最大费用。
删边技巧是,在建这S->v,v->u,u->T 三条边时,先建中间那条,统计该点连到S几次,减去连到T点几次,结果若为正,则与S连一条边,容量就是几次,若负,同理。
至于why it works!得好好想想~
画几个点验证了一下发现,如果一个原图中的环(权值大于0)值得取,那么流会自动流向该环原图中的负权边。而如果不值得取,那么会流向原图中的正权边。因为我们是用sum(负值)加上那个费用(正值),所以当该环要取时,则自动减去那些负权,不取呢,会自动减去那些正权(而那些负权的完全没取到)。不懂就画个环出来验证吧。
1 #include <bits/stdc++.h>
2 #define LL long long
3 #define pii pair<int,int>
4 #define pdi pair<double,int>
5 #define INF 0x7f7f7f7f
6 using namespace std;
7 const int N=200;
8 int x[N], y[N], rudu[N];
9 int earn, lost, n;
10 vector<int> vect[N], vec[N];
11 double sum;
12
13 struct node
14 {
15 int from, to, cap, flow;
16 double val;
17 node(){};
18 node(int from,int to,double val,int cap,int flow):from(from),to(to),val(val),cap(cap),flow(flow){};
19 }edge[90000];
20 int edge_cnt;
21
22 void add_node(int from,int to,double val,int cap,int flow)
23 {
24 edge[edge_cnt]=node(from, to, val, cap, flow );
25 vec[from].push_back(edge_cnt++);
26 }
27
28 void build_graph()
29 {
30 for(int i=1; i<=n; i++)
31 {
32 for(int j=0; j<vect[i].size(); j++)
33 {
34 int t=vect[i][j];
35 double v= lost - sqrt( pow(x[i]-x[t],2)+pow(y[i]-y[t],2) )*earn;
36
37 if(v<0)
38 {
39 add_node(t, i, -v, 1, 0 ); //反边
40 add_node(i, t, v, 0, 0 );
41 sum+=v;
42 rudu[t]++,rudu[i]--;
43 }
44 else
45 {
46 add_node(i, t, v, 1, 0);
47 add_node(t, i, -v, 0, 0);
48 }
49 }
50 }
51 for(int i=1; i<=n; i++)
52 {
53 if(rudu[i]>0)
54 {
55 add_node(0, i, 0, rudu[i], 0);
56 add_node(i, 0, 0, 0, 0);
57 }
58 if(rudu[i]<0)
59 {
60 add_node(i, n+1, 0, -rudu[i], 0);
61 add_node(n+1, i, 0, 0, 0);
62 }
63 }
64 }
65
66 int flow[N], path[N], inq[N];
67 double cost[N];
68
69 double spfa(int s,int e)
70 {
71 deque<int> que(1,s);
72 cost[s]=0;
73 flow[s]=INF;
74 inq[s]=1;
75 while(!que.empty())
76 {
77 int x=que.front();
78 que.pop_front();
79 inq[x]=0;
80 for(int i=0; i<vec[x].size(); i++)
81 {
82 node e=edge[vec[x][i]];
83 if(e.cap>e.flow && cost[e.to]>cost[e.from]+e.val )
84 {
85 flow[e.to]=min(flow[e.from],e.cap-e.flow);
86 cost[e.to]=cost[e.from]+e.val;
87 path[e.to]=vec[x][i];
88 if(!inq[e.to])
89 {
90 inq[e.to]=1;
91 que.push_back(e.to);
92 }
93 }
94 }
95 }
96 return cost[e];
97 }
98
99 double mcmf(int s,int e)
100 {
101 double ans_cost=0.0;
102 while(true)
103 {
104 memset(flow,0,sizeof(flow));
105 memset(inq,0,sizeof(inq));
106 memset(path,0,sizeof(path));
107 for(int i=0; i<=e; i++) cost[i]=1e39;
108
109 double tmp=spfa(s,e); //返回费用
110 if(tmp>1e38) return ans_cost;
111 ans_cost+=tmp;
112
113 int ed=e;
114 while(ed!=s)
115 {
116 int t=path[ed];
117 edge[t].flow+=flow[n+1];
118 edge[t^1].flow-=flow[n+1];
119 ed=edge[t].from;
120 }
121 }
122 }
123
124 int main()
125 {
126 freopen("input.txt", "r", stdin);
127 int b, j=0;
128 while(scanf("%d", &n), n)
129 {
130 scanf("%d%d",&earn,&lost);
131 for(int i=0; i<=n+1; i++) vect[i].clear();
132 for(int i=0; i<=n+1; i++) vec[i].clear();
133 memset(edge,0,sizeof(edge));
134 memset(rudu,0,sizeof(rudu));
135 edge_cnt=0;
136 sum=0;
137
138 for(int i=1; i<=n; i++)
139 {
140 scanf("%d%d",&x[i],&y[i]);
141 while(scanf("%d",&b), b) vect[i].push_back(b); //原图邻接表
142 }
143 build_graph();
144 printf("Case %d: %.2f\n", ++j, -(mcmf(0,n+1)+sum)+0.0000001 );
145 }
146 return 0;
147 } AC代码