一些闲话:旅行传送门
题意:给你一个含有 \(k\) 个节点,编号从 \(0\) 至 \(k-1\) 的计算集群,以及一组已知到达时间与处理时间的请求(亦从 \(0\) 开始编号)。
当每个请求到达时,它会优先进入第 (\(i\) % \(k\)) 个节点,若当前节点正忙,则根据开放定址法去找下一个空闲节点(如果最终都没能找到空闲的节点,该请求将被忽略)。
现在问你在发送完这组请求后,哪些节点处理的请求数量最多?
题目分析:显然,请求的结束时间(即节点可以被重新启用的时间)= 到达时间 + 处理时间。
先考虑暴力的做法,新请求到来时扫一遍当前节点,如果有节点满足条件(节点内请求的结束时间 \(\leq\) 当前请求的到达时间)就进行更新,时间复杂度约为 \(O(nk)\) ,必 \(T\)。
这里采取线段树+二分查询优化,时间复杂度 \(O(nlogk)\) ,具体看图:
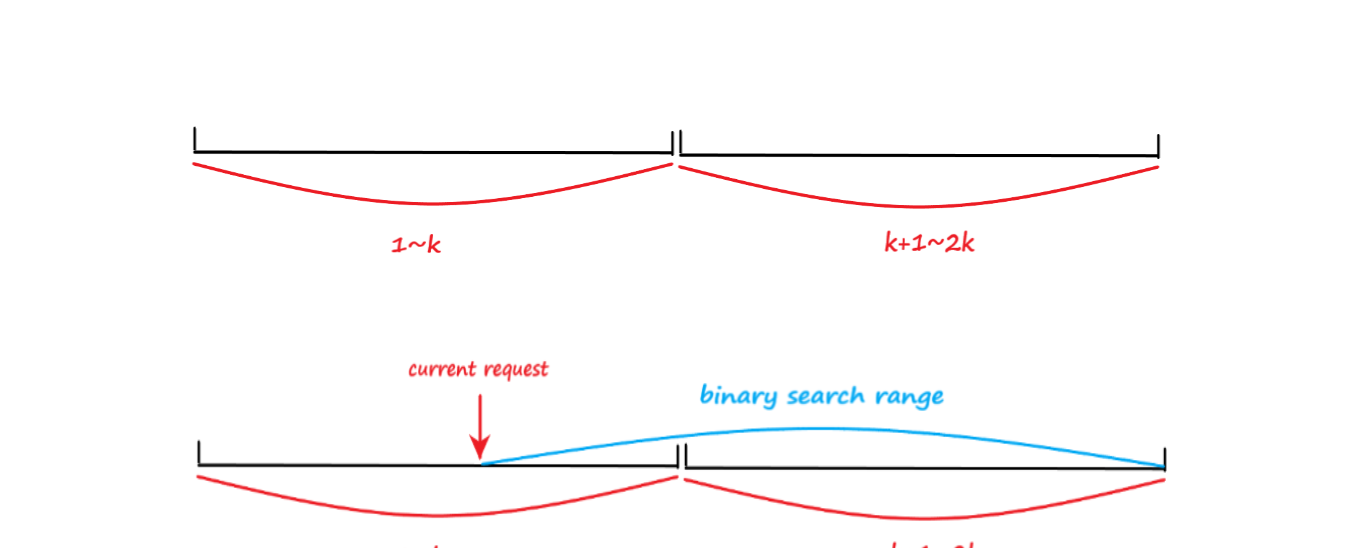
线段树维护区间最小值,单点修改,区间查询
根据最小值进行二分,为了方便查询我拷贝了一份节点(也可以先查 \(i\) ~ \(k-1\) ,再查 \(0\) ~ \(i-1\) ),更新时同时更新两个就好。
注意输出格式,行尾无空格(白 PE 六发,真的傻逼)
AC代码:
题意:给你 \(n\) 个点和 \(m\) 次操作,每次操作令区间 \([l, r]\) 中的点两两相连构成一张边权为 \(w\) 的完全图,求要得到最小生成树所需删除边的边权总和。
题目分析:将所有操作按边权降序排序,接下来按区间覆盖问题来做就好,最终得到的最小生成树一定是一条链,答案即为总边权减去最小生成树的权重,线段树与分块均可,分块要跑得快一些。
AC代码(线段树):
AC代码(分块):
题意:给你两个圆心分别为 \((a,b)\) 与 \((2a,0)\) 的圆 \(A\) 、 \(B\) ,半径均为 \(r\) 的圆,现从原点出发,问先经过圆 \(A\) 再经过圆 \(B\) 的最短路径是多少?
题目分析:分两种情况讨论,具体看图和代码:
题意:给你 \(n\) 个点的坐标,这些点构成了一些三角形和线段。每次询问一个点所有的邻点与所在图形的编号。
题目分析:最开始 \(cx\) 理解的意思就是对的,我也想过坐标是不是没用,但可惜没能猜透出题人的心思,往复杂的方面去想了,赛后交流的时候发现有几支队伍也想歪了,大家都在考虑怎么判断某个点包不包含在其它三角形内,一致认为这是个几何题,各种叉乘去搞。
结果笑死,哪有我们想的这么高大上,用 \(map\) 直接记录就完事了。md搁着猜谜呢,和出题人心意不相通还写不了题了。
题意:给你一个序列 \(S\) 和一个数 \(A\) ,找出序列中所有与 \(A\) 的差值 \(\leq r\) 的元素,降序输出。
题目分析:签到题,降序排列后 \(O(n)\) 扫一遍就好,难点主要在处理输入数据上。
题意:给你一张初始全为白点的空图,按照时间顺序建图,建图过程中会将白点染成红黑色,求相邻两次询问间新增的红黑路(红点到黑点)的路径长的异或和,红黑路的路径长指的是路径上每个点的编号乘以当前长度的总和。
题目分析:离线算法,记录每个操作当前的时间戳。先 \(dfs\) 标记所有能到达黑点的点,然后构造新图,只把有用的边连上,再对每个红点进行 \(dfs\) 计算其构成的每条红黑路的路径长,根据之前记录的时间戳来更新答案以保证正确性。最后维护个前缀异或和,对每个询问输出 \(ans_{q[i]} \bigoplus ans_{q[i-1]}\) 即可。
题意:模拟题,给你一张有向图,每次询问从节点 \(i\) 开始按指定方向走最终到达的点。
题目分析:阅读理解+模拟,跟着题意来就好,越界就判定丢包。