一些閑話:旅行傳送門
題意:給你一個含有 \(k\) 個節點,編号從 \(0\) 至 \(k-1\) 的計算叢集,以及一組已知到達時間與處理時間的請求(亦從 \(0\) 開始編号)。
當每個請求到達時,它會優先進入第 (\(i\) % \(k\)) 個節點,若目前節點正忙,則根據開放定址法去找下一個空閑節點(如果最終都沒能找到空閑的節點,該請求将被忽略)。
現在問你在發送完這組請求後,哪些節點處理的請求數量最多?
題目分析:顯然,請求的結束時間(即節點可以被重新啟用的時間)= 到達時間 + 處理時間。
先考慮暴力的做法,新請求到來時掃一遍目前節點,如果有節點滿足條件(節點内請求的結束時間 \(\leq\) 目前請求的到達時間)就進行更新,時間複雜度約為 \(O(nk)\) ,必 \(T\)。
這裡采取線段樹+二分查詢優化,時間複雜度 \(O(nlogk)\) ,具體看圖:
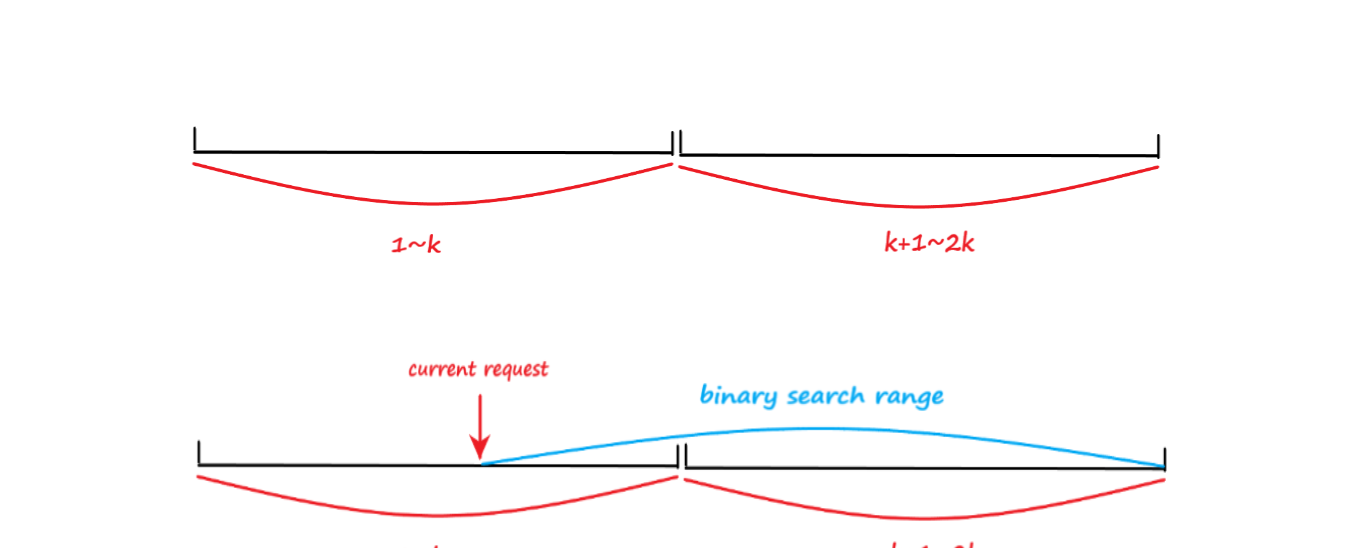
線段樹維護區間最小值,單點修改,區間查詢
根據最小值進行二分,為了友善查詢我拷貝了一份節點(也可以先查 \(i\) ~ \(k-1\) ,再查 \(0\) ~ \(i-1\) ),更新時同時更新兩個就好。
注意輸出格式,行尾無空格(白 PE 六發,真的傻逼)
AC代碼:
題意:給你 \(n\) 個點和 \(m\) 次操作,每次操作令區間 \([l, r]\) 中的點兩兩相連構成一張邊權為 \(w\) 的完全圖,求要得到最小生成樹所需删除邊的邊權總和。
題目分析:将所有操作按邊權降序排序,接下來按區間覆寫問題來做就好,最終得到的最小生成樹一定是一條鍊,答案即為總邊權減去最小生成樹的權重,線段樹與分塊均可,分塊要跑得快一些。
AC代碼(線段樹):
AC代碼(分塊):
題意:給你兩個圓心分别為 \((a,b)\) 與 \((2a,0)\) 的圓 \(A\) 、 \(B\) ,半徑均為 \(r\) 的圓,現從原點出發,問先經過圓 \(A\) 再經過圓 \(B\) 的最短路徑是多少?
題目分析:分兩種情況讨論,具體看圖和代碼:
題意:給你 \(n\) 個點的坐标,這些點構成了一些三角形和線段。每次詢問一個點所有的鄰點與所在圖形的編号。
題目分析:最開始 \(cx\) 了解的意思就是對的,我也想過坐标是不是沒用,但可惜沒能猜透出題人的心思,往複雜的方面去想了,賽後交流的時候發現有幾支隊伍也想歪了,大家都在考慮怎麼判斷某個點包不包含在其它三角形内,一緻認為這是個幾何題,各種叉乘去搞。
結果笑死,哪有我們想的這麼高大上,用 \(map\) 直接記錄就完事了。md擱着猜謎呢,和出題人心意不相通還寫不了題了。
題意:給你一個序列 \(S\) 和一個數 \(A\) ,找出序列中所有與 \(A\) 的內插補點 \(\leq r\) 的元素,降序輸出。
題目分析:簽到題,降序排列後 \(O(n)\) 掃一遍就好,難點主要在處理輸入資料上。
題意:給你一張初始全為白點的空圖,按照時間順序建圖,建圖過程中會将白點染成紅黑色,求相鄰兩次詢問間新增的紅黑路(紅點到黑點)的路徑長的異或和,紅黑路的路徑長指的是路徑上每個點的編号乘以目前長度的總和。
題目分析:離線算法,記錄每個操作目前的時間戳。先 \(dfs\) 标記所有能到達黑點的點,然後構造新圖,隻把有用的邊連上,再對每個紅點進行 \(dfs\) 計算其構成的每條紅黑路的路徑長,根據之前記錄的時間戳來更新答案以保證正确性。最後維護個字首異或和,對每個詢問輸出 \(ans_{q[i]} \bigoplus ans_{q[i-1]}\) 即可。
題意:模拟題,給你一張有向圖,每次詢問從節點 \(i\) 開始按指定方向走最終到達的點。
題目分析:閱讀了解+模拟,跟着題意來就好,越界就判定丢包。