题意:给你两个正整数 \(n\) 和 \(s\) 。求由 \(n\) 个非负整数组成的总和为 \(s\) 的序列的最大中位数。
题目分析:显然,令前 $ \frac{n+1}{2}-1$ 个数为 \(0\) 时序列有最大中位数。
AC代码:
题意:设二进制字符串的 \(MEX\) 为字符串中未出现的 \(0\) 、 \(1\) 或 \(2\) 中最小的数字。
现在给你一个字符串 \(s\) ,你可以将 \(s\) 切成任意几份(分成几个子串),求所有子串片段的最小 \(MEX\) 总和。
题目分析:要使得 \(MEX\) 总和最小,显然要将连续的 \(0\) 切分出来。另外要明确的是 \(ans \leq 2\) ,因此比较连续段 \(0\) 的段数和 \(2\) 的大小即可。
题意:给你一个 \(2 \times n\) 的 \(01\) 矩阵, 你可以将该矩阵切成任意几份(分成几个 \(2 \times m\) 的子矩阵),求所有子矩阵的最大 \(MEX\) 总和。
题目分析:我们不妨枚举下 \(2 \times 2\) 的 \(01\) 矩阵的所有情况,\({\begin{bmatrix}1&0\\0&1\end{bmatrix}}\) 、 \({\begin{bmatrix}1&0\\0&0\end{bmatrix}}\) 、 \({\begin{bmatrix}1&1\\0&1\end{bmatrix}}\) 、 \({\begin{bmatrix}0&0\\1&0\end{bmatrix}}\) 、 \({\begin{bmatrix}0&1\\1&1\end{bmatrix}}\) 、 \({\begin{bmatrix}0&1\\0&1\end{bmatrix}}\) ,不难发现,\({\begin{bmatrix}1\\1\end{bmatrix}}\) 本身对答案是没有贡献的,但它与 \({\begin{bmatrix}0\\0\end{bmatrix}}\) 组合时,却能使 \({\begin{bmatrix}0\\0\end{bmatrix}}\) 的贡献 \(+1\) ,而 \({\begin{bmatrix}1\\0\end{bmatrix}}\) (\({\begin{bmatrix}0\\1\end{bmatrix}}\))的贡献本身已经是 \(2\) 了,与其它的 \(1 \times 2\) 矩阵组合时也不会产生多的贡献。那么我们的思路已经很明确了,先找出主矩阵中的所有 \({\begin{bmatrix}1\\1\end{bmatrix}}\) 子矩阵,与它旁边空闲的 \({\begin{bmatrix}0\\0\end{bmatrix}}\) 组合,最后再扫一遍将未组合的 \(1 \times 2\) 矩阵切分出来加上贡献即是最终答案。
题意:有 \(n \times m\) 个人和 \(n \times m\) 个座位,座位编号如题面所示。每个人的视力对应一个值 \(a_i\) ,\(a_i\)越小的人座位越靠前。从第 \(1\) 个人至 第 \(n \times m\) 个人依次就座,每个人就座时的代价为该行经过的人数,求如何安排座位可使代价最小化。
题目分析: 显然,对某一行来说,若同一个数值连续出现,那么他们之间不会产生任何代价(把编号较小的放进靠后的位置)。此外,数值大的在数值小的之前出现,也不会产生任何代价(数值大的先坐进靠后的位置去了)。那么会对答案产生贡献的不就一种情况了吗?数值小的在数值大的之前!这是什么?正序对?树状数组走起。
需要注意: \(a_i\)很大,离散一下。
题目分析:与 \(easy\) \(version\) 不同的是现在有多行了,基本思路还是树状数组求正序对,一开始想的是先按数值排个序,然后按顺序每行选出 \(m\) 个人,再对这 \(m\) 个人按编号排序,用D1的做法求他们对答案的贡献,可惜超时了 ┑(﹀_﹀)┍
后来去luogu逛了一圈发现有julao也用的是树状数组的思路,但julao的处理方式明显比我更优,这里开个旅行传送门,在此不过多赘述了。
题意:给你一棵树,树的芽满足以下条件:
非根非叶子节点
所有子节点均为叶子节点
你可以剪掉一棵芽(删去芽与其父节点的连边)并放在其他任意节点上,该操作可以进行任意次,现在要你最小化叶子节点数目,并求最小值是多少。
题目分析:结论题,首先将整棵树尽可能多地拆成芽并放在根节点上形成一棵深度 \(\leq 3\) 的树,因为每个带有 \(x\) 个叶子节点的芽在嫁接到另一节点上后,对答案的贡献是 \(x-1\) ,所以保持其中一个芽不动,其它芽顺着它连成一条链即是最优解。
图是从luogu偷的,但画的着实好,实在忍不住。
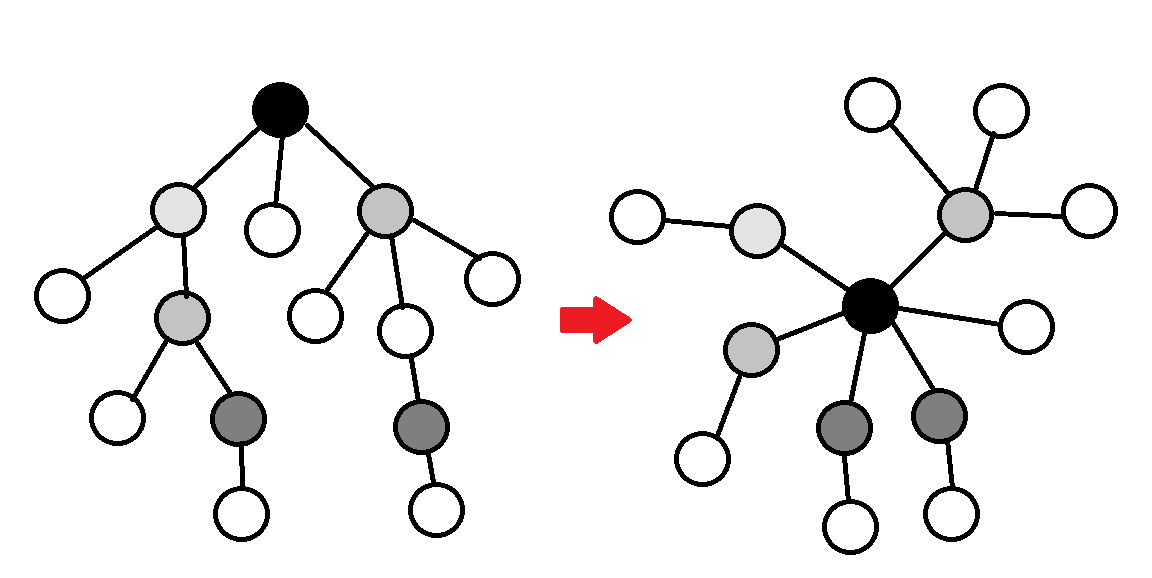
为了观感更好,我在原图连成链的时候把嫁接的地方换成虚线了。