題意:給你兩個正整數 \(n\) 和 \(s\) 。求由 \(n\) 個非負整數組成的總和為 \(s\) 的序列的最大中位數。
題目分析:顯然,令前 $ \frac{n+1}{2}-1$ 個數為 \(0\) 時序列有最大中位數。
AC代碼:
題意:設二進制字元串的 \(MEX\) 為字元串中未出現的 \(0\) 、 \(1\) 或 \(2\) 中最小的數字。
現在給你一個字元串 \(s\) ,你可以将 \(s\) 切成任意幾份(分成幾個子串),求所有子串片段的最小 \(MEX\) 總和。
題目分析:要使得 \(MEX\) 總和最小,顯然要将連續的 \(0\) 切分出來。另外要明确的是 \(ans \leq 2\) ,是以比較連續段 \(0\) 的段數和 \(2\) 的大小即可。
題意:給你一個 \(2 \times n\) 的 \(01\) 矩陣, 你可以将該矩陣切成任意幾份(分成幾個 \(2 \times m\) 的子矩陣),求所有子矩陣的最大 \(MEX\) 總和。
題目分析:我們不妨枚舉下 \(2 \times 2\) 的 \(01\) 矩陣的所有情況,\({\begin{bmatrix}1&0\\0&1\end{bmatrix}}\) 、 \({\begin{bmatrix}1&0\\0&0\end{bmatrix}}\) 、 \({\begin{bmatrix}1&1\\0&1\end{bmatrix}}\) 、 \({\begin{bmatrix}0&0\\1&0\end{bmatrix}}\) 、 \({\begin{bmatrix}0&1\\1&1\end{bmatrix}}\) 、 \({\begin{bmatrix}0&1\\0&1\end{bmatrix}}\) ,不難發現,\({\begin{bmatrix}1\\1\end{bmatrix}}\) 本身對答案是沒有貢獻的,但它與 \({\begin{bmatrix}0\\0\end{bmatrix}}\) 組合時,卻能使 \({\begin{bmatrix}0\\0\end{bmatrix}}\) 的貢獻 \(+1\) ,而 \({\begin{bmatrix}1\\0\end{bmatrix}}\) (\({\begin{bmatrix}0\\1\end{bmatrix}}\))的貢獻本身已經是 \(2\) 了,與其它的 \(1 \times 2\) 矩陣組合時也不會産生多的貢獻。那麼我們的思路已經很明确了,先找出主矩陣中的所有 \({\begin{bmatrix}1\\1\end{bmatrix}}\) 子矩陣,與它旁邊空閑的 \({\begin{bmatrix}0\\0\end{bmatrix}}\) 組合,最後再掃一遍将未組合的 \(1 \times 2\) 矩陣切分出來加上貢獻即是最終答案。
題意:有 \(n \times m\) 個人和 \(n \times m\) 個座位,座位編号如題面所示。每個人的視力對應一個值 \(a_i\) ,\(a_i\)越小的人座位越靠前。從第 \(1\) 個人至 第 \(n \times m\) 個人依次就座,每個人就座時的代價為該行經過的人數,求如何安排座位可使代價最小化。
題目分析: 顯然,對某一行來說,若同一個數值連續出現,那麼他們之間不會産生任何代價(把編号較小的放進靠後的位置)。此外,數值大的在數值小的之前出現,也不會産生任何代價(數值大的先坐進靠後的位置去了)。那麼會對答案産生貢獻的不就一種情況了嗎?數值小的在數值大的之前!這是什麼?正序對?樹狀數組走起。
需要注意: \(a_i\)很大,離散一下。
題目分析:與 \(easy\) \(version\) 不同的是現在有多行了,基本思路還是樹狀數組求正序對,一開始想的是先按數值排個序,然後按順序每行選出 \(m\) 個人,再對這 \(m\) 個人按編号排序,用D1的做法求他們對答案的貢獻,可惜逾時了 ┑(﹀_﹀)┍
後來去luogu逛了一圈發現有julao也用的是樹狀數組的思路,但julao的處理方式明顯比我更優,這裡開個旅行傳送門,在此不過多贅述了。
題意:給你一棵樹,樹的芽滿足以下條件:
非根非葉子節點
所有子節點均為葉子節點
你可以剪掉一棵芽(删去芽與其父節點的連邊)并放在其他任意節點上,該操作可以進行任意次,現在要你最小化葉子節點數目,并求最小值是多少。
題目分析:結論題,首先将整棵樹盡可能多地拆成芽并放在根節點上形成一棵深度 \(\leq 3\) 的樹,因為每個帶有 \(x\) 個葉子節點的芽在嫁接到另一節點上後,對答案的貢獻是 \(x-1\) ,是以保持其中一個芽不動,其它芽順着它連成一條鍊即是最優解。
圖是從luogu偷的,但畫的着實好,實在忍不住。
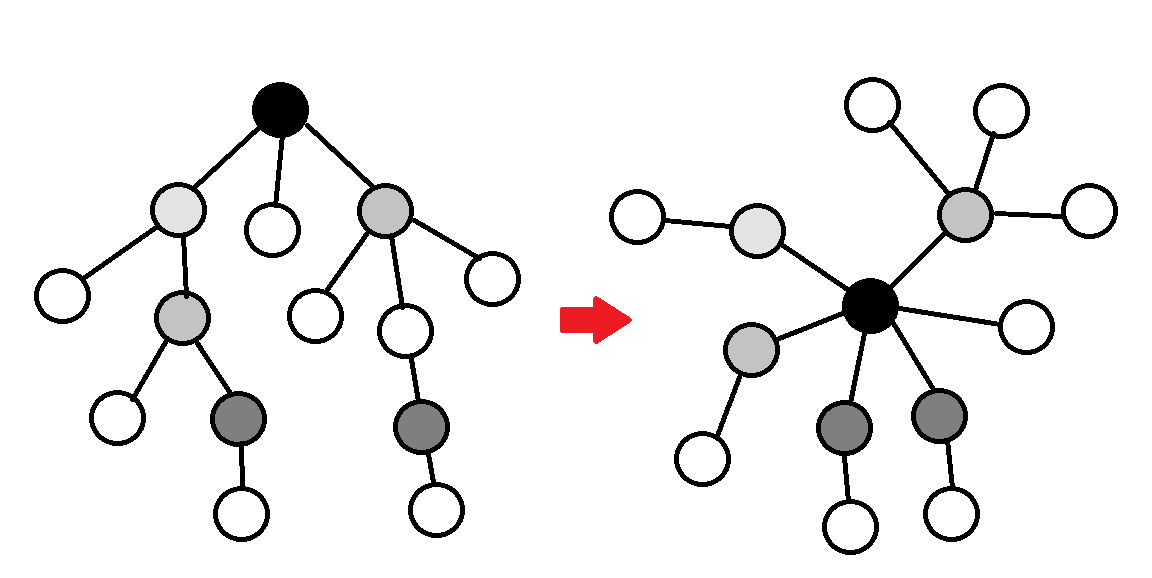
為了觀感更好,我在原圖連成鍊的時候把嫁接的地方換成虛線了。