Python实现RNN定义RNN结构predict方法train方法测试结果

一般的前馈神经网络中, 输出的结果只与当前输入有关与历史状态无关, 而递归神经网络(Recurrent Neural Network, RNN)神经元的历史输出参与下一次预测.

本文中我们将尝试使用RNN处理二进制加法问题: 两个加数作为两个序列输入, 从右向左处理加数序列.和的某一位不仅与加数的当前位有关, 还与上一位的进位有关.

词语的含义与上下文有关, 未来的状态不仅与当前相关还与历史状态相关. 因为这种性质, RNN非常适合自然语言处理和时间序列分析等任务.

RNN与前馈神经网络最大的不同在于多了一条反馈回路, 将RNN展开即可得到前馈神经网络.

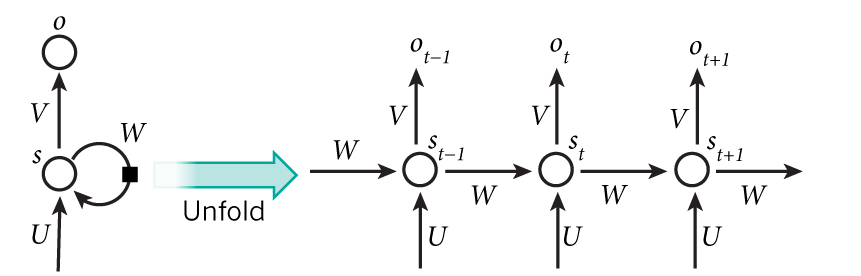
RNN同样采用BP算法进行训练, 误差反向传播时需要逆向通过反馈回路.

定义输出层误差为:

Ej=sigmod′(Oj)(TjOj)=Oj(1Oj)(TjOj)Ej=sigmod′(Oj)(TjOj)=Oj(1Oj)(TjOj)

其中, OjOj是预测输出, TjTj是参考输出.

因为隐含层没有参考输出, 采用下一层的误差加权和代替TjOjTjOj. 对于隐含层神经元而言这里的下一层可能是输出层, 也可能是其自身.

更多关于BP算法的内容可以参考BP神经网络与Python实现

完整的代码可以在rnn.py找到.

因为篇幅原因, 相关工具函数请在完整源码中查看, 文中不再赘述.

这里我们定义一个简单的3层递归神经网络, 隐含层神经元的输出只与当前状态以及上一个状态有关.

定义<code>RNN</code>类:

这里定义了几个比较重要的矩阵:

<code>input_weights</code>: 输入层和隐含层之间的连接权值矩阵.

<code>output_weights</code>: 隐含层和输出层之间的连接权值矩阵

<code>hidden_weights</code>: 隐含层反馈回路权值矩阵, 反馈回路从一个隐含层神经元出发到另一个隐含层神经元.

因为本文的RNN只有一阶反馈, 因此只需要一个反馈回路权值矩阵.对于n阶RNN来说需要n个反馈权值矩阵.

定义<code>test()</code>方法作为示例代码的入口:

<code>do_train</code>方法仅进行一次训练, 这里我们生成了20000组训练数据每组数据仅执行一次训练.

<code>predict</code>方法执行一次前馈过程, 以给出预测输出序列.

初始化<code>guess</code>向量作为预测输出, <code>hidden_layer_history</code>列表保存隐含层的历史值用于计算反馈的影响.

自右向左遍历序列, 对每个元素进行一次前馈.

上面这行代码是前馈的核心, 隐含层的输入由两部分组成:

来自输入层的输入<code>np.dot(x, self.input_weights)</code>.

来自上一个状态的反馈<code>np.dot(hidden_layer_history[-1], self.hidden_weights)</code>.

上面这行代码执行输出层的计算, 因为二进制加法的原因这里对输出结果进行了取整.

定义<code>train</code>方法来控制迭代过程:

<code>do_train</code>方法实现了具体的训练逻辑:

训练逻辑中两次遍历序列, 第一次遍历执行前馈过程并计算输出层误差.

第二次遍历计算隐含层误差, 下列代码是计算隐含层误差的核心:

因为隐含层在前馈过程中参与了两次, 所以会有两层神经元反向传播误差:

输出层传递的误差加权和<code>output_delta.dot(self.output_weights.T)</code>

反馈回路中下一层隐含神经元传递的误差加权和<code>future_hidden_layer_delta.dot(self.hidden_weights.T)</code>

将两部分误差求和然后乘自身输出的sigmoid导数<code>sigmoid_derivative(hidden_layer)</code>即为隐含层误差, 这里与普通前馈网络中的BP算法是一致的.

执行<code>test()</code>方法可以看到测试结果:

预测精度还是很令人满意的.

本文转自帅气的头头博客51CTO博客，原文链接http://blog.51cto.com/12902932/1925707如需转载请自行联系原作者

sshpp