Python實作RNN定義RNN結構predict方法train方法測試結果

一般的前饋神經網絡中, 輸出的結果隻與目前輸入有關與曆史狀态無關, 而遞歸神經網絡(Recurrent Neural Network, RNN)神經元的曆史輸出參與下一次預測.

本文中我們将嘗試使用RNN處理二進制加法問題: 兩個加數作為兩個序列輸入, 從右向左處理加數序列.和的某一位不僅與加數的目前位有關, 還與上一位的進位有關.

詞語的含義與上下文有關, 未來的狀态不僅與目前相關還與曆史狀态相關. 因為這種性質, RNN非常适合自然語言處理和時間序列分析等任務.

RNN與前饋神經網絡最大的不同在于多了一條回報回路, 将RNN展開即可得到前饋神經網絡.

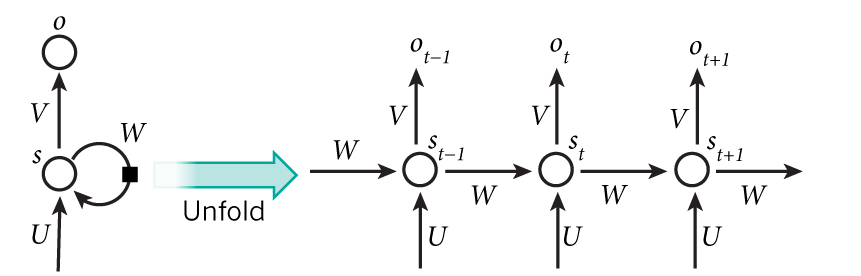
RNN同樣采用BP算法進行訓練, 誤差反向傳播時需要逆向通過回報回路.

定義輸出層誤差為:

Ej=sigmod′(Oj)(TjOj)=Oj(1Oj)(TjOj)Ej=sigmod′(Oj)(TjOj)=Oj(1Oj)(TjOj)

其中, OjOj是預測輸出, TjTj是參考輸出.

因為隐含層沒有參考輸出, 采用下一層的誤差權重和代替TjOjTjOj. 對于隐含層神經元而言這裡的下一層可能是輸出層, 也可能是其自身.

更多關于BP算法的内容可以參考BP神經網絡與Python實作

完整的代碼可以在rnn.py找到.

因為篇幅原因, 相關工具函數請在完整源碼中檢視, 文中不再贅述.

這裡我們定義一個簡單的3層遞歸神經網絡, 隐含層神經元的輸出隻與目前狀态以及上一個狀态有關.

定義<code>RNN</code>類:

這裡定義了幾個比較重要的矩陣:

<code>input_weights</code>: 輸入層和隐含層之間的連接配接權值矩陣.

<code>output_weights</code>: 隐含層和輸出層之間的連接配接權值矩陣

<code>hidden_weights</code>: 隐含層回報回路權值矩陣, 回報回路從一個隐含層神經元出發到另一個隐含層神經元.

因為本文的RNN隻有一階回報, 是以隻需要一個回報回路權值矩陣.對于n階RNN來說需要n個回報權值矩陣.

定義<code>test()</code>方法作為示例代碼的入口:

<code>do_train</code>方法僅進行一次訓練, 這裡我們生成了20000組訓練資料每組資料僅執行一次訓練.

<code>predict</code>方法執行一次前饋過程, 以給出預測輸出序列.

初始化<code>guess</code>向量作為預測輸出, <code>hidden_layer_history</code>清單儲存隐含層的曆史值用于計算回報的影響.

自右向左周遊序列, 對每個元素進行一次前饋.

上面這行代碼是前饋的核心, 隐含層的輸入由兩部分組成:

來自輸入層的輸入<code>np.dot(x, self.input_weights)</code>.

來自上一個狀态的回報<code>np.dot(hidden_layer_history[-1], self.hidden_weights)</code>.

上面這行代碼執行輸出層的計算, 因為二進制加法的原因這裡對輸出結果進行了取整.

定義<code>train</code>方法來控制疊代過程:

<code>do_train</code>方法實作了具體的訓練邏輯:

訓練邏輯中兩次周遊序列, 第一次周遊執行前饋過程并計算輸出層誤差.

第二次周遊計算隐含層誤差, 下列代碼是計算隐含層誤差的核心:

因為隐含層在前饋過程中參與了兩次, 是以會有兩層神經元反向傳播誤差:

輸出層傳遞的誤差權重和<code>output_delta.dot(self.output_weights.T)</code>

回報回路中下一層隐含神經元傳遞的誤差權重和<code>future_hidden_layer_delta.dot(self.hidden_weights.T)</code>

将兩部分誤差求和然後乘自身輸出的sigmoid導數<code>sigmoid_derivative(hidden_layer)</code>即為隐含層誤差, 這裡與普通前饋網絡中的BP算法是一緻的.

執行<code>test()</code>方法可以看到測試結果:

預測精度還是很令人滿意的.

本文轉自帥氣的頭頭部落格51CTO部落格，原文連結http://blog.51cto.com/12902932/1925707如需轉載請自行聯系原作者

sshpp