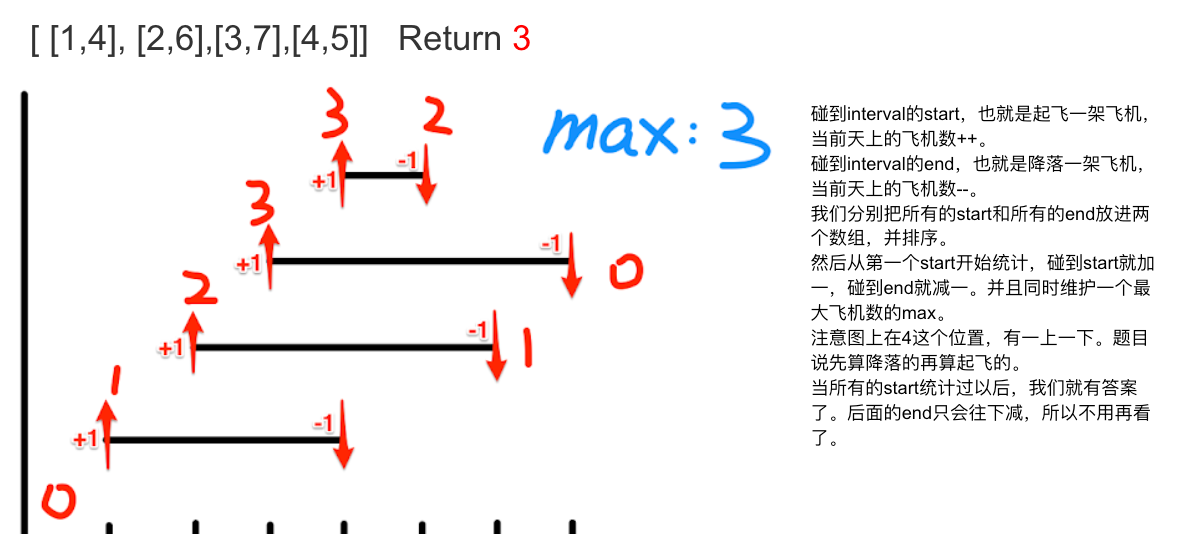
391 · 数飞机
描述
给出飞机的起飞和降落时间的列表,用序列 <code>interval</code> 表示. 请计算出天上同时最多有多少架飞机?
如果多架飞机降落和起飞在同一时刻,我们认为降落有优先权。
样例
样例 1:
样例 2:
Given an array of meeting time intervals consisting of start and end times <code>[[s1,e1],[s2,e2],...]</code> (si < ei), determine if a person could attend all meetings.
Example 1:
Example 2:
919 · Meeting Rooms II
Given an array of meeting time intervals consisting of start and end times <code>[[s1,e1],[s2,e2],...] (si < ei)</code>, find the minimum number of conference rooms required.
Example1
Example2
第二种解法:
56. Merge Intervals
Given an array of <code>intervals</code> where <code>intervals[i] = [starti, endi]</code>, merge all overlapping intervals, and return an array of the non-overlapping intervals that cover all the intervals in the input.
Example 1:
Example 2:
Constraints:
<code>1 <= intervals.length <= 104</code>
<code>intervals[i].length == 2</code>
<code>0 <= starti <= endi <= 104</code>
Given a sorted list of disjoint <code>intervals</code>, each interval <code>intervals[i] = [a, b]</code> represents the set of real numbers <code>x</code> such that <code>a <= x < b</code>.
We remove the intersections between any interval in <code>intervals</code> and the interval <code>toBeRemoved</code>.
Return a sorted list of <code>intervals</code> after all such removals.
Example 1:
Example 2:
Constraints:
<code>1 <= intervals.length <= 10^4</code>
<code>-10^9 <= intervals[i][0] < intervals[i][1] <= 10^9</code>
57. Insert Interval
You are given an array of non-overlapping intervals <code>intervals</code> where <code>intervals[i] = [starti, endi]</code> represent the start and the end of the <code>ith</code> interval and <code>intervals</code> is sorted in ascending order by <code>starti</code>. You are also given an interval <code>newInterval = [start, end]</code> that represents the start and end of another interval.
Insert <code>newInterval</code> into <code>intervals</code> such that <code>intervals</code> is still sorted in ascending order by <code>starti</code> and <code>intervals</code> still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return <code>intervals</code> after the insertion.
Example 1:
Example 2:
Example 3:
Example 4:
Example 5:
Constraints:
<code>0 <= intervals.length <= 104</code>
<code>intervals[i].length == 2</code>
<code>0 <= starti <= endi <= 105</code>
<code>intervals</code> is sorted by <code>starti</code> in ascending order.
<code>newInterval.length == 2</code>
<code>0 <= start <= end <= 105</code>
435. Non-overlapping Intervals
Given an array of intervals <code>intervals</code> where <code>intervals[i] = [starti, endi]</code>, return the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.
Example 1:
Example 2:
Example 3:
Constraints:
<code>1 <= intervals.length <= 105</code>
<code>intervals[i].length == 2</code>
<code>-5 * 104 <= starti < endi <= 5 * 104</code>
解法: greedy
1288. Remove Covered Intervals
Given an array <code>intervals</code> where <code>intervals[i] = [li, ri]</code> represent the interval <code>[li, ri)</code>, remove all intervals that are covered by another interval in the list.
The interval <code>[a, b)</code> is covered by the interval <code>[c, d)</code> if and only if <code>c <= a</code> and <code>b <= d</code>.
Return the number of remaining intervals.
Example 1:
Example 2:
Example 3:
Example 4:
Example 5:
Constraints:
<code>1 <= intervals.length <= 1000</code>
<code>intervals[i].length == 2</code>
<code>0 <= li <= ri <= 105</code>
All the given intervals are unique.
352. Data Stream as Disjoint Intervals
Given a data stream input of non-negative integers <code>a1, a2, ..., an</code>, summarize the numbers seen so far as a list of disjoint intervals.
Implement the <code>SummaryRanges</code> class:
<code>SummaryRanges()</code> Initializes the object with an empty stream.
<code>void addNum(int val)</code> Adds the integer <code>val</code> to the stream.
<code>int[][] getIntervals()</code> Returns a summary of the integers in the stream currently as a list of disjoint intervals <code>[starti, endi]</code>.
Example 1:
Constraints:
<code>0 <= val <= 104</code>
At most <code>3 * 104</code> calls will be made to <code>addNum</code> and <code>getIntervals</code>.
Follow up: What if there are lots of merges and the number of disjoint intervals is small compared to the size of the data stream?
Given the availability time slots arrays <code>slots1</code> and <code>slots2</code> of two people and a meeting duration <code>duration</code>, return the earliest time slot that works for both of them and is of duration <code>duration</code>.
If there is no common time slot that satisfies the requirements, return an empty array.
The format of a time slot is an array of two elements <code>[start, end]</code> representing an inclusive time range from <code>start</code> to <code>end</code>.
It is guaranteed that no two availability slots of the same person intersect with each other. That is, for any two time slots <code>[start1, end1]</code> and <code>[start2, end2]</code> of the same person, either <code>start1 > end2</code> or <code>start2 > end1</code>.
Example 1:
Example 2:
Constraints:
<code>1 <= slots1.length, slots2.length <= 10^4</code>
<code>slots1[i].length, slots2[i].length == 2</code>
<code>slots1[i][0] < slots1[i][1]</code>
<code>slots2[i][0] < slots2[i][1]</code>
<code>0 <= slots1[i][j], slots2[i][j] <= 10^9</code>
<code>1 <= duration <= 10^6 </code>
解法一:数飞机
解法二:
986. Interval List Intersections
You are given two lists of closed intervals, <code>firstList</code> and <code>secondList</code>, where <code>firstList[i] = [starti, endi]</code> and <code>secondList[j] = [startj, endj]</code>. Each list of intervals is pairwise disjoint and in sorted order.
Return the intersection of these two interval lists.
A closed interval <code>[a, b]</code> (with <code>a <= b</code>) denotes the set of real numbers <code>x</code> with <code>a <= x <= b</code>.
The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of <code>[1, 3]</code> and <code>[2, 4]</code> is <code>[2, 3]</code>.
Example 1:
Example 2:
Example 3:
Example 4:
Constraints:
<code>0 <= firstList.length, secondList.length <= 1000</code>
<code>firstList.length + secondList.length >= 1</code>
<code>0 <= starti < endi <= 109</code>
<code>endi < starti+1</code>
<code>0 <= startj < endj <= 109</code>
<code>endj < startj+1</code>
这个题实际就是上一道题稍微改变了一下
解法一:数飞机
解法二:
850 · 员工空闲时间
描述
我们得到一个员工的<code>schedule</code>列表,代表每个员工工作时间。
每个员工有一个不重合时段的列表 <code>Intervals</code>,这些时段按序排列。
返回一个所有员工共有的空闲时段的列表,并按序排列。
我们的<code>Intervals</code>是一个一维数组,其中每两个数表示一个区间,即<code>[1,2,8,10]</code>表示这个员工的工作时间是<code>[1,2]</code>和<code>[8,10]</code>。
并且,我们的答案不会包括像[5,5]这样的,因为它们的长度是0。
<code>schedule</code> 和 <code>schedule[i]</code> 为长度范围在 <code>[1, 100]</code>的列表。
<code>0 <= schedule[i].start < schedule[i].end <= 10^8</code>。
样例
样例 1:
样例 2:
解法: 这题感觉压根算不上hard,直接数飞机!!!
218. The Skyline Problem
Hard
A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.
The geometric information of each building is given in the array <code>buildings</code> where <code>buildings[i] = [lefti, righti, heighti]</code>:
<code>lefti</code> is the x coordinate of the left edge of the <code>ith</code> building.
<code>righti</code> is the x coordinate of the right edge of the <code>ith</code> building.
<code>heighti</code> is the height of the <code>ith</code> building.
You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height <code>0</code>.
The skyline should be represented as a list of "key points" sorted by their x-coordinate in the form <code>[[x1,y1],[x2,y2],...]</code>. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate <code>0</code> and is used to mark the skyline's termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline's contour.
Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, <code>[...,[2 3],[4 5],[7 5],[11 5],[12 7],...]</code> is not acceptable; the three lines of height 5 should be merged into one in the final output as such: <code>[...,[2 3],[4 5],[12 7],...]</code>
Example 1:
Example 2:
Constraints:
<code>1 <= buildings.length <= 104</code>
<code>0 <= lefti < righti <= 231 - 1</code>
<code>1 <= heighti <= 231 - 1</code>
<code>buildings</code> is sorted by <code>lefti</code> in non-decreasing order.
数飞机:
更简化的写法:
1882. Process Tasks Using Servers
Medium
You are given two 0-indexed integer arrays <code>servers</code> and <code>tasks</code> of lengths <code>n</code> and <code>m</code> respectively. <code>servers[i]</code> is the weight of the <code>ith</code> server, and <code>tasks[j]</code> is the time needed to process the <code>jth</code> task in seconds.
Tasks are assigned to the servers using a task queue. Initially, all servers are free, and the queue is empty.
At second <code>j</code>, the <code>jth</code> task is inserted into the queue (starting with the <code>0th</code> task being inserted at second <code>0</code>). As long as there are free servers and the queue is not empty, the task in the front of the queue will be assigned to a free server with the smallest weight, and in case of a tie, it is assigned to a free server with the smallest index.
If there are no free servers and the queue is not empty, we wait until a server becomes free and immediately assign the next task. If multiple servers become free at the same time, then multiple tasks from the queue will be assigned in order of insertion following the weight and index priorities above.
A server that is assigned task <code>j</code> at second <code>t</code> will be free again at second <code>t + tasks[j]</code>.
Build an array <code>ans</code> of length <code>m</code>, where <code>ans[j]</code> is the index of the server the <code>jth</code> task will be assigned to.
Return the array <code>ans</code>.
Example 1:
Example 2:
Constraints:
<code>servers.length == n</code>
<code>tasks.length == m</code>
<code>1 <= n, m <= 2 * 105</code>
<code>1 <= servers[i], tasks[j] <= 2 * 105</code>
Given an array of meeting time intervals consisting of start and end times <code>[[s1,e1],[s2,e2],...]</code> (si < ei), determine if a person could attend all meetings.
Example 1:
Example 2:
Given the availability time slots arrays <code>slots1</code> and <code>slots2</code> of two people and a meeting duration <code>duration</code>, return the earliest time slot that works for both of them and is of duration <code>duration</code>.
If there is no common time slot that satisfies the requirements, return an empty array.
The format of a time slot is an array of two elements <code>[start, end]</code> representing an inclusive time range from <code>start</code> to <code>end</code>.
It is guaranteed that no two availability slots of the same person intersect with each other. That is, for any two time slots <code>[start1, end1]</code> and <code>[start2, end2]</code> of the same person, either <code>start1 > end2</code> or <code>start2 > end1</code>.
Example 1:
Example 2:
Constraints:
<code>1 <= slots1.length, slots2.length <= 10^4</code>
<code>slots1[i].length, slots2[i].length == 2</code>
<code>slots1[i][0] < slots1[i][1]</code>
<code>slots2[i][0] < slots2[i][1]</code>
<code>0 <= slots1[i][j], slots2[i][j] <= 10^9</code>
<code>1 <= duration <= 10^6 </code>
解法一:数飞机
解法二:
986. Interval List Intersections
You are given two lists of closed intervals, <code>firstList</code> and <code>secondList</code>, where <code>firstList[i] = [starti, endi]</code> and <code>secondList[j] = [startj, endj]</code>. Each list of intervals is pairwise disjoint and in sorted order.
Return the intersection of these two interval lists.
A closed interval <code>[a, b]</code> (with <code>a <= b</code>) denotes the set of real numbers <code>x</code> with <code>a <= x <= b</code>.
The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of <code>[1, 3]</code> and <code>[2, 4]</code> is <code>[2, 3]</code>.
Example 1:
Example 2:
Example 3:
Example 4:
Constraints:
<code>0 <= firstList.length, secondList.length <= 1000</code>
<code>firstList.length + secondList.length >= 1</code>
<code>0 <= starti < endi <= 109</code>
<code>endi < starti+1</code>
<code>0 <= startj < endj <= 109</code>
<code>endj < startj+1</code>
这个题实际就是上一道题稍微改变了一下
解法一:数飞机
解法二:
850 · 员工空闲时间
描述
我们得到一个员工的<code>schedule</code>列表,代表每个员工工作时间。
每个员工有一个不重合时段的列表 <code>Intervals</code>,这些时段按序排列。
返回一个所有员工共有的空闲时段的列表,并按序排列。
我们的<code>Intervals</code>是一个一维数组,其中每两个数表示一个区间,即<code>[1,2,8,10]</code>表示这个员工的工作时间是<code>[1,2]</code>和<code>[8,10]</code>。
并且,我们的答案不会包括像[5,5]这样的,因为它们的长度是0。
<code>schedule</code> 和 <code>schedule[i]</code> 为长度范围在 <code>[1, 100]</code>的列表。
<code>0 <= schedule[i].start < schedule[i].end <= 10^8</code>。
样例
样例 1:
样例 2:
解法: 这题感觉压根算不上hard,直接数飞机!!!
218. The Skyline Problem
Hard
A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.
The geometric information of each building is given in the array <code>buildings</code> where <code>buildings[i] = [lefti, righti, heighti]</code>:
<code>lefti</code> is the x coordinate of the left edge of the <code>ith</code> building.
<code>righti</code> is the x coordinate of the right edge of the <code>ith</code> building.
<code>heighti</code> is the height of the <code>ith</code> building.
You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height <code>0</code>.
The skyline should be represented as a list of "key points" sorted by their x-coordinate in the form <code>[[x1,y1],[x2,y2],...]</code>. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate <code>0</code> and is used to mark the skyline's termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline's contour.
Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, <code>[...,[2 3],[4 5],[7 5],[11 5],[12 7],...]</code> is not acceptable; the three lines of height 5 should be merged into one in the final output as such: <code>[...,[2 3],[4 5],[12 7],...]</code>
Example 1:
Example 2:
Constraints:
<code>1 <= buildings.length <= 104</code>
<code>0 <= lefti < righti <= 231 - 1</code>
<code>1 <= heighti <= 231 - 1</code>
<code>buildings</code> is sorted by <code>lefti</code> in non-decreasing order.
数飞机:
更简化的写法:
1882. Process Tasks Using Servers
Medium
You are given two 0-indexed integer arrays <code>servers</code> and <code>tasks</code> of lengths <code>n</code> and <code>m</code> respectively. <code>servers[i]</code> is the weight of the <code>ith</code> server, and <code>tasks[j]</code> is the time needed to process the <code>jth</code> task in seconds.
Tasks are assigned to the servers using a task queue. Initially, all servers are free, and the queue is empty.
At second <code>j</code>, the <code>jth</code> task is inserted into the queue (starting with the <code>0th</code> task being inserted at second <code>0</code>). As long as there are free servers and the queue is not empty, the task in the front of the queue will be assigned to a free server with the smallest weight, and in case of a tie, it is assigned to a free server with the smallest index.
If there are no free servers and the queue is not empty, we wait until a server becomes free and immediately assign the next task. If multiple servers become free at the same time, then multiple tasks from the queue will be assigned in order of insertion following the weight and index priorities above.
A server that is assigned task <code>j</code> at second <code>t</code> will be free again at second <code>t + tasks[j]</code>.
Build an array <code>ans</code> of length <code>m</code>, where <code>ans[j]</code> is the index of the server the <code>jth</code> task will be assigned to.
Return the array <code>ans</code>.
Example 1:
Example 2:
Constraints:
<code>servers.length == n</code>
<code>tasks.length == m</code>
<code>1 <= n, m <= 2 * 105</code>
<code>1 <= servers[i], tasks[j] <= 2 * 105</code>