作者:Vamei 出处:http://www.cnblogs.com/vamei 严禁转载。
统计最开始的主要任务就是描述数据。正如我们在统计概述中提到的,群体的数据可能包含大量的数字,往往让人读起来头昏脑涨。电影《美丽心灵》中,数学家纳什不自觉地沉浸在一串数字中。这样的电影桥段经常让观众感到惭愧。但真相是,每个人的注意力和短期记忆都很有限,只能集中在很少量的信息。数据描述就是要用一定的方法来提取少量信息,从而让人更容易明白数据的含义。数据描述的方法可以分为两大门类,即群体参数和数据绘图。两者都起到了简化信息作用,从而让数据变得更加易读。
群体参数是用一些数字来表示群体的特征。我们在统计概述中已经介绍了两个群体参数,群体平均值和群体方差。群体平均值(population mean)反映群体总体状况,定义如下:
$$\mu=\frac{1}{N} \sum_{i=0}^N x_i$$
群体方差(population variance)反映群体的离散状况,定义如下:
$$\sigma^2=\frac{1}{N} \sum_{i=0}^N (x_i - \mu)^2$$
方差的平方根,即[$\sigma$],称为群体标准差(standard deviation)。从物理的角度上来看,平均值和标准差所带的单位,都和原始数据相同。在多数统计案例中,大部分的群体数据会落在平均值加减一个标准差的范围内。
还有一些参数要通过对群体成员进行排序才能获得。比如群体的最大值(max)和最小值(min)。在这一类参数中,还经常会用到中位数(median)和四分位数(quartile)。对成员进行排序后,最中间成员的取值就是中位数。如果群体总数为偶数,那么中位数就是中间两个成员取值的平均值。按照大于还是小于中位数的标准,成员可以划分为数目相同的两组。对这两组再求中位数,就可以获得下四分位数(lower quartile)和上四分位数(upper quartile)。[$Q_1$]和[$Q_3$]之间的距离,称为四分位距(IQR,inter quartile range),也是一个常见的群体参数。我们用下面符号表示:
$$Q_1 = lower\ quartile$$
$$Q_2 = M = median$$
$$Q_3 = upper\ quartile$$
$$IQR = Q_3 - Q_1$$
中位数是按照50%划分数据,下四分位数是按照25%划分数据,上四分位数是按照75%划分数据。其实,中位数和四分位数都属于百分位数(percentile)。我们用任意比例来划分数据,从而取得百分位数。把数据按数值大小排列,处于p%位置的成员的取值,称第p百分位数。
我们可以计算出湘北高中学生身高数据的描述参数:
代码如下:
数据绘图利用了人类对形状的敏感。在通过数据绘图,我们可以将数字转换的几何图形,让数据中的信息变得更容易消化。数据绘图曾经是个费时费力的手工活,但计算机图形的发展让数据绘图变得简单。这两年更是新兴起“数据可视化”,用很多炫目的手段来呈现数据。但说到底,经典的绘图只有那么几种,如饼图、散点图、曲线图。“数据可视化”中的创新手法,也只不过是从这些经典方法中衍生出来的。由于人们已经形成了约定俗成的数据绘图习惯,绘图方式上的过度创新甚至会误导读者。所以,这里出现的,也是经典的统计绘图形式。
由于这一系列统计教程主要用Python,我将基于Matplotlib介绍几种经典的数据绘图方式。Matplotlib是基于numpy的一套Python工具包,提供了丰富的数据绘图工具。当然,Matplotlib并非唯一的选择。有的统计学家更偏爱R语言,而Web开发者流行使用D3.js。熟悉了一种绘图工具后,总可以触类旁通,很快地掌握其他的工具。
我们将以2011年几个国家的GDP数据为例子,看看如何绘制经典的饼图和条形图。数据如下:
这是一个只有10个成员的群体。群体成员的取值即该成员的2011年的GDP总额。这里的单位是(百万美元)。
我们先来绘制饼图 (pie plot)。绘制饼图就像分披萨。整个披萨代表成员取值的总和。每个成员根据自己取值的大小,拿相应大小的那块儿披萨。把上面的数据绘制成饼图:
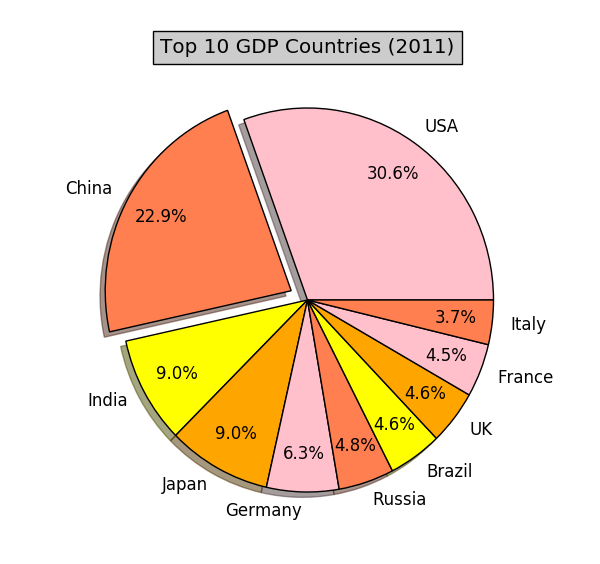
从图中可以看到,在这场“分大饼”的游戏中,美国和中国占了大的份额。不过,人们从饼图中读到的只是比例,没办法获得成员的具体数值。因此,饼图适用于表示成员取值在总和中所占的百分比。上面饼图的代码如下:
饼图的缺点是无法表达成员的具体取值,而条形图(bar plot)正是用于呈现数据取值。条形图绘制的是一个个竖直的长条,这个长条的高度就代表了取值。还是用上面2011年GDP的数据,用条形图绘制出来就是:
条形图有水平和竖直两个方向。水平方向上标出了每个竖条对应的国家,竖直方向标出了GDP的数值。这样,读者就可以读出每个国家的GDP了。上面绘图的代码如下:
基本的条形图就是这样一种标记数据取值的绘图方式。如果想知道数值,那么可以直接从数据表中读出来,大可以不必画条形图。统计绘图中更常用一种从条形图中衍生出来的绘图方式:直方图(histogram)。直方图会对群体数据进行预处理,然后再把预处理结果用条形图的形式画出来。举一个简单的例子,在绘图中呈现湘北高中所有学生的身高数据。想象一下,如果让每个学生的身高对应一个竖条,那么图上就会密密麻麻地挤满数千个竖条,很难提供有价值的信息。但如果画成直方图的形式,看起来就会如下图:
在这幅图中,横坐标成了身高取值。每个竖条的宽度对应了一定的身高范围,例如170cm到172cm。竖条的高度,对应了身高在该区间内的学生数。因此,直方图先进行了一次分组的预处理,然后用条形图的办法,画出了每个组中包含的成员总数。在分组的处理中,一些原始信息丢失,以至于从竖条中没办法读出学生的具体身高。但得到简化的信息变得更容易理解。看了这个图之后,我们可以有信心地说,大部分学生的身高在170cm附近。而身高低于150cm或者身高高于190cm的学生占据的比例很少。如果一个人只是读原始数据,很难短时间内获得上面的结论。
直方图绘图程序如下:
代码中的hist()函数用于绘制直方图,其中的50说明了要生成的区间分组的个数。根据需要,你也可以具体说明在哪些区间形成分组。
趋势图(run chart)又称为折线图,经常用于呈现时间序列。时间序列是随着时间产生的一组数据,比如上海去年每一天的气温,再比如中国最近50年的GDP。趋势图会把相邻时间点的数据用直线连接起来,从而从视觉上体现出数据随时间变化的特征。趋势图在生活中很常见,例如股民就经常会通过类似的图来了解股价随时间的变化。下面是中国1960-2015年GDP的趋势图:
在这个趋势图中很容易看到,中国的GDP随着时间快速增长。绘图的代码如下:
上面的绘图方式,本质上都是二维统计图。饼图是国别和比例的二维信息,直方图体现了身高和人数的二维关系,趋势图的两个维度则是时间和GDP。散点图(scatter plot)是一种最直接的表达二维关系的绘图方式。二维绘图的其他方式,都可以理解成散点图的一个变种。
散点图通过在二维平面上标记出数据点来呈现数据。如果我们想研究湘北高中学生身高和体重的关系,就可以在表示“身高-体重”的二维平面上,标记出所有成员的数据:
在这个散点图中,二维平面的横向代表身高,纵向代表体重,每一个点代表了一个学生。通过这个点对应的横纵坐标,就可以读出该学生的身高和体重。散点图可以直观地呈现所有数据,因此上可以告诉我们整体分布上有何特征。我们从图中可以看到,体重大体上随着身高增长而增长。
绘图代码如下:
散点是通过二维的位置来表示数据。在应用中,还可以通过散点的大小来表示三维的数据。这种进化了的散点图称为泡泡图(bubble plot)。除了散点的大小,泡泡图有时还会用散点的颜色来表达更高维度的信息。
我们来看泡泡图的一个例子。下图中绘出了亚洲主要城市的人口。城市的位置包含了二维的信息,即经度和纬度。此外,人口构成了第三维。我们用散点的大小来表示这一维度。
数据如下:
代码中使用了matplotlib的Basemap模块来绘制地图:
之前的绘图方式侧重点在原始数据。还有一些绘图是为了呈现群体参数,比如箱形图(box plot)。比如湘北高中身高数据绘制成箱形图:
如图中标注的,箱形图体现的主要是中位数和四分位数。上下四分位数构成了箱子,其中包含了一半的数据成员。此外,上下还有两个边界,位于箱子的上下边缘各外推1.5个箱子高度的位置。如果外推1.5个箱子位置超出了数据库的极值,那么边界换成极值的高度。否则,将有数据点超出边界。这些数据点被认为是异常值(outlier),用散点的方式画出。
箱形图体现了一个思路,就是在绘制原始数据的同时画出群体参数,从而辅助我们理解数据。比如,我们可以在直方图中标出平均值和标准差:
尽管这里说明了一些常用的数据绘图方法,但数据绘图的过程中有很多人为创作的因素在。因此,同一个数据库,甚至同一种绘图形式,都可能产生多种多样的数据图像。不同的数据图像,在传递信息的有效性上,会产生不小的差别。怎样画好数据图呢?我根据自己的经验,总结了下面几个标准:
确定目的。尽管在研究过程中,我们会画出大量的数据图,但在展示数据图时,要有所侧重。
在标题中说明一张数据图的主要内容。
标明每一个坐标轴,并标明坐标的刻度和单位。
如果没有坐标轴,需要用图例来说明读数。例如在泡泡图中用图例说明泡泡大小所代表的读数。
在图中标注附加的图像元素,如代表平均值的标示线、代表拟合的虚线曲线等。
备份数据、图像文件和相关代码。
在介绍一副数据图时,也可以遵循一定的顺序:
一句话说明画了什么:“这幅图描绘了湘北高中学生身高分布。”
说明坐标轴:“图中横轴代表了身高,纵轴代表了人数。”
说明主要图像元素的含义:“每个竖条对应一定的身高区间。竖条的高度,代表了该身高区间内学生的人数。”
说明次要图像元素的含义:“红线代表了学生的平均身高。”
引导读者深入解读:“可以看到,学生身高大多集中在平均值附近……”
当然,对于存在人为创作因素的数据绘图来说,也没有定法。但建立一定的流程,能提高绘图的效率。所以我也建议你建立自己的绘图流程。
在这一篇文章里,我主要用参数和绘图呈现群体的数据。类似的方法还经常用于呈现样品数据。由于在描绘样品时需要涉及到统计推断,所以我把样品描绘的方法放在将在统计推断的相关文章中讲解。
如果你想更多地了解Matplotlib,可以参考官方文档,以及我以前写的这篇文章:matplotlib核心剖析 。
欢迎继续阅读“数据科学”系列文章
如果你喜欢这篇文章,欢迎推荐。