作者:Vamei 出處:http://www.cnblogs.com/vamei 嚴禁轉載。
統計最開始的主要任務就是描述資料。正如我們在統計概述中提到的,群體的資料可能包含大量的數字,往往讓人讀起來頭昏腦漲。電影《美麗心靈》中,數學家納什不自覺地沉浸在一串數字中。這樣的電影橋段經常讓觀衆感到慚愧。但真相是,每個人的注意力和短期記憶都很有限,隻能集中在很少量的資訊。資料描述就是要用一定的方法來提取少量資訊,進而讓人更容易明白資料的含義。資料描述的方法可以分為兩大門類,即群體參數和資料繪圖。兩者都起到了簡化資訊作用,進而讓資料變得更加易讀。
群體參數是用一些數字來表示群體的特征。我們在統計概述中已經介紹了兩個群體參數,群體平均值和群體方差。群體平均值(population mean)反映群體總體狀況,定義如下:
$$\mu=\frac{1}{N} \sum_{i=0}^N x_i$$
群體方差(population variance)反映群體的離散狀況,定義如下:
$$\sigma^2=\frac{1}{N} \sum_{i=0}^N (x_i - \mu)^2$$
方差的平方根,即[$\sigma$],稱為群體标準差(standard deviation)。從實體的角度上來看,平均值和标準差所帶的機關,都和原始資料相同。在多數統計案例中,大部分的群體資料會落在平均值加減一個标準差的範圍内。
還有一些參數要通過對群體成員進行排序才能獲得。比如群體的最大值(max)和最小值(min)。在這一類參數中,還經常會用到中位數(median)和四分位數(quartile)。對成員進行排序後,最中間成員的取值就是中位數。如果群體總數為偶數,那麼中位數就是中間兩個成員取值的平均值。按照大于還是小于中位數的标準,成員可以劃分為數目相同的兩組。對這兩組再求中位數,就可以獲得下四分位數(lower quartile)和上四分位數(upper quartile)。[$Q_1$]和[$Q_3$]之間的距離,稱為四分位距(IQR,inter quartile range),也是一個常見的群體參數。我們用下面符号表示:
$$Q_1 = lower\ quartile$$
$$Q_2 = M = median$$
$$Q_3 = upper\ quartile$$
$$IQR = Q_3 - Q_1$$
中位數是按照50%劃分資料,下四分位數是按照25%劃分資料,上四分位數是按照75%劃分資料。其實,中位數和四分位數都屬于百分位數(percentile)。我們用任意比例來劃分資料,進而取得百分位數。把資料按數值大小排列,處于p%位置的成員的取值,稱第p百分位數。
我們可以計算出湘北高中學生身高資料的描述參數:
代碼如下:
資料繪圖利用了人類對形狀的敏感。在通過資料繪圖,我們可以将數字轉換的幾何圖形,讓資料中的資訊變得更容易消化。資料繪圖曾經是個費時費力的手工活,但計算機圖形的發展讓資料繪圖變得簡單。這兩年更是新興起“資料可視化”,用很多炫目的手段來呈現資料。但說到底,經典的繪圖隻有那麼幾種,如餅圖、散點圖、曲線圖。“資料可視化”中的創新手法,也隻不過是從這些經典方法中衍生出來的。由于人們已經形成了約定俗成的資料繪圖習慣,繪圖方式上的過度創新甚至會誤導讀者。是以,這裡出現的,也是經典的統計繪圖形式。
由于這一系列統計教程主要用Python,我将基于Matplotlib介紹幾種經典的資料繪圖方式。Matplotlib是基于numpy的一套Python工具包,提供了豐富的資料繪圖工具。當然,Matplotlib并非唯一的選擇。有的統計學家更偏愛R語言,而Web開發者流行使用D3.js。熟悉了一種繪圖工具後,總可以觸類旁通,很快地掌握其他的工具。
我們将以2011年幾個國家的GDP資料為例子,看看如何繪制經典的餅圖和條形圖。資料如下:
這是一個隻有10個成員的群體。群體成員的取值即該成員的2011年的GDP總額。這裡的機關是(百萬美元)。
我們先來繪制餅圖 (pie plot)。繪制餅圖就像分披薩。整個披薩代表成員取值的總和。每個成員根據自己取值的大小,拿相應大小的那塊兒披薩。把上面的資料繪制成餅圖:
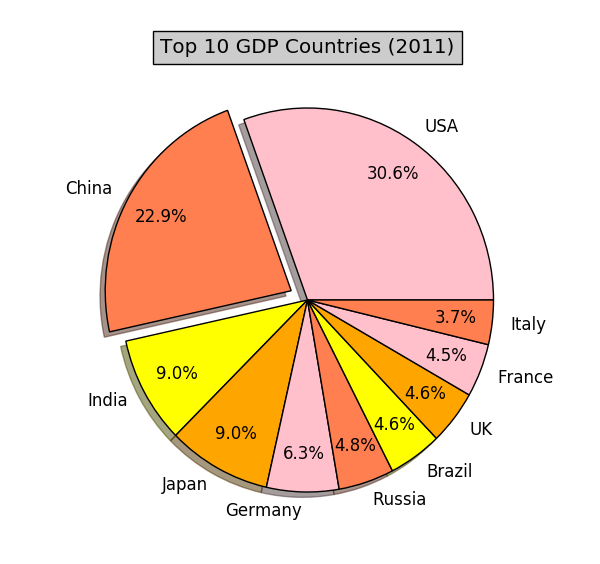
從圖中可以看到,在這場“分大餅”的遊戲中,美國和中國占了大的份額。不過,人們從餅圖中讀到的隻是比例,沒辦法獲得成員的具體數值。是以,餅圖适用于表示成員取值在總和中所占的百分比。上面餅圖的代碼如下:
餅圖的缺點是無法表達成員的具體取值,而條形圖(bar plot)正是用于呈現資料取值。條形圖繪制的是一個個豎直的長條,這個長條的高度就代表了取值。還是用上面2011年GDP的資料,用條形圖繪制出來就是:
條形圖有水準和豎直兩個方向。水準方向上标出了每個豎條對應的國家,豎直方向标出了GDP的數值。這樣,讀者就可以讀出每個國家的GDP了。上面繪圖的代碼如下:
基本的條形圖就是這樣一種标記資料取值的繪圖方式。如果想知道數值,那麼可以直接從資料表中讀出來,大可以不必畫條形圖。統計繪圖中更常用一種從條形圖中衍生出來的繪圖方式:直方圖(histogram)。直方圖會對群體資料進行預處理,然後再把預處理結果用條形圖的形式畫出來。舉一個簡單的例子,在繪圖中呈現湘北高中所有學生的身高資料。想象一下,如果讓每個學生的身高對應一個豎條,那麼圖上就會密密麻麻地擠滿數千個豎條,很難提供有價值的資訊。但如果畫成直方圖的形式,看起來就會如下圖:
在這幅圖中,橫坐标成了身高取值。每個豎條的寬度對應了一定的身高範圍,例如170cm到172cm。豎條的高度,對應了身高在該區間内的學生數。是以,直方圖先進行了一次分組的預處理,然後用條形圖的辦法,畫出了每個組中包含的成員總數。在分組的進行中,一些原始資訊丢失,以至于從豎條中沒辦法讀出學生的具體身高。但得到簡化的資訊變得更容易了解。看了這個圖之後,我們可以有信心地說,大部分學生的身高在170cm附近。而身高低于150cm或者身高高于190cm的學生占據的比例很少。如果一個人隻是讀原始資料,很難短時間内獲得上面的結論。
直方圖繪圖程式如下:
代碼中的hist()函數用于繪制直方圖,其中的50說明了要生成的區間分組的個數。根據需要,你也可以具體說明在哪些區間形成分組。
趨勢圖(run chart)又稱為折線圖,經常用于呈現時間序列。時間序列是随着時間産生的一組資料,比如上海去年每一天的氣溫,再比如中國最近50年的GDP。趨勢圖會把相鄰時間點的資料用直線連接配接起來,進而從視覺上展現出資料随時間變化的特征。趨勢圖在生活中很常見,例如股民就經常會通過類似的圖來了解股價随時間的變化。下面是中國1960-2015年GDP的趨勢圖:
在這個趨勢圖中很容易看到,中國的GDP随着時間快速增長。繪圖的代碼如下:
上面的繪圖方式,本質上都是二維統計圖。餅圖是國别和比例的二維資訊,直方圖展現了身高和人數的二維關系,趨勢圖的兩個次元則是時間和GDP。散點圖(scatter plot)是一種最直接的表達二維關系的繪圖方式。二維繪圖的其他方式,都可以了解成散點圖的一個變種。
散點圖通過在二維平面上标記出資料點來呈現資料。如果我們想研究湘北高中學生身高和體重的關系,就可以在表示“身高-體重”的二維平面上,标記出所有成員的資料:
在這個散點圖中,二維平面的橫向代表身高,縱向代表體重,每一個點代表了一個學生。通過這個點對應的橫縱坐标,就可以讀出該學生的身高和體重。散點圖可以直覺地呈現所有資料,是以上可以告訴我們整體分布上有何特征。我們從圖中可以看到,體重大體上随着身高增長而增長。
繪圖代碼如下:
散點是通過二維的位置來表示資料。在應用中,還可以通過散點的大小來表示三維的資料。這種進化了的散點圖稱為泡泡圖(bubble plot)。除了散點的大小,泡泡圖有時還會用散點的顔色來表達更高次元的資訊。
我們來看泡泡圖的一個例子。下圖中繪出了亞洲主要城市的人口。城市的位置包含了二維的資訊,即經度和緯度。此外,人口構成了第三維。我們用散點的大小來表示這一次元。
資料如下:
代碼中使用了matplotlib的Basemap子產品來繪制地圖:
之前的繪圖方式側重點在原始資料。還有一些繪圖是為了呈現群體參數,比如箱形圖(box plot)。比如湘北高中身高資料繪制成箱形圖:
如圖中标注的,箱形圖展現的主要是中位數和四分位數。上下四分位數構成了箱子,其中包含了一半的資料成員。此外,上下還有兩個邊界,位于箱子的上下邊緣各外推1.5個箱子高度的位置。如果外推1.5個箱子位置超出了資料庫的極值,那麼邊界換成極值的高度。否則,将有資料點超出邊界。這些資料點被認為是異常值(outlier),用散點的方式畫出。
箱形圖展現了一個思路,就是在繪制原始資料的同時畫出群體參數,進而輔助我們了解資料。比如,我們可以在直方圖中标出平均值和标準差:
盡管這裡說明了一些常用的資料繪圖方法,但資料繪圖的過程中有很多人為創作的因素在。是以,同一個資料庫,甚至同一種繪圖形式,都可能産生多種多樣的資料圖像。不同的資料圖像,在傳遞資訊的有效性上,會産生不小的差别。怎樣畫好資料圖呢?我根據自己的經驗,總結了下面幾個标準:
确定目的。盡管在研究過程中,我們會畫出大量的資料圖,但在展示資料圖時,要有所側重。
在标題中說明一張資料圖的主要内容。
标明每一個坐标軸,并标明坐标的刻度和機關。
如果沒有坐标軸,需要用圖例來說明讀數。例如在泡泡圖中用圖例說明泡泡大小所代表的讀數。
在圖中标注附加的圖像元素,如代表平均值的标示線、代表拟合的虛線曲線等。
備份資料、圖像檔案和相關代碼。
在介紹一副資料圖時,也可以遵循一定的順序:
一句話說明畫了什麼:“這幅圖描繪了湘北高中學生身高分布。”
說明坐标軸:“圖中橫軸代表了身高,縱軸代表了人數。”
說明主要圖像元素的含義:“每個豎條對應一定的身高區間。豎條的高度,代表了該身高區間内學生的人數。”
說明次要圖像元素的含義:“紅線代表了學生的平均身高。”
引導讀者深入解讀:“可以看到,學生身高大多集中在平均值附近……”
當然,對于存在人為創作因素的資料繪圖來說,也沒有定法。但建立一定的流程,能提高繪圖的效率。是以我也建議你建立自己的繪圖流程。
在這一篇文章裡,我主要用參數和繪圖呈現群體的資料。類似的方法還經常用于呈現樣品資料。由于在描繪樣品時需要涉及到統計推斷,是以我把樣品描繪的方法放在将在統計推斷的相關文章中講解。
如果你想更多地了解Matplotlib,可以參考官方文檔,以及我以前寫的這篇文章:matplotlib核心剖析 。
歡迎繼續閱讀“資料科學”系列文章
如果你喜歡這篇文章,歡迎推薦。