基于欧式距离的分割和基于区域生长的分割本质上都是用区分邻里关系远近来完成的。由于点云数据提供了更高维度的数据,故有很多信息可以提取获得。欧几里得算法使用邻居之间距离作为判定标准,而区域生长算法则利用了法线,曲率,颜色等信息来判断点云是否应该聚成一类。
(1)欧几里德算法
具体的实现方法大致是:
找到空间中某点p10,有kdTree找到离他最近的n个点,判断这n个点到p的距离。将距离小于阈值r的点p12,p13,p14....放在类Q里
在 Q\p10 里找到一点p12,重复1
在 Q\p10,p12 找到一点,重复1,找到p22,p23,p24....全部放进Q里
当 Q 再也不能有新点加入了,则完成搜索了
因为点云总是连成片的,很少有什么东西会浮在空中来区分。但是如果结合此算法可以应用很多东东。比如
半径滤波删除离群点
采样一致找到桌面或者除去滤波
当然,一旦桌面被剔除,桌上的物体就自然成了一个个的浮空点云团。就能够直接用欧几里德算法进行分割了,这样就可以提取出我们想要识别的东西
在这里我们就可以使用提取平面,利用聚类的方法平面去掉再显示剩下的所有聚类的结果,在这里也就是有关注我的微信公众号的小伙伴向我请教,说虽然都把平面和各种非平面提取出来了,但是怎么把非平面的聚类对象可视化出来呢?
哈哈,刚开始我也以为没有例程实现这样的可视化,也许比较难吧,但是仔细一想,提取出来的聚类的对象都是单独的显示在相对与源文件不变的位置所以我们直接相加就应该可以实现阿~所以废话没多说我就直接写程序,的确可视化的结果就是我想要的结果
那么我们看一下我的代码吧
编译生成可执行文件后结果如下
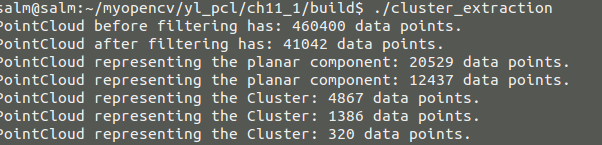
那么我们查看以下源文件可视化的结果
再可视化我们聚类后除了平面的可视化的结果,从中可以看出效果还是很明显的。
当然总结一下,我们在实际应用的过程中可能没那么轻松,因为我们要根据实际的点云的大小来设置相关的参数,如果参数错误就不太能实现现在的效果。
所以对实际应用中参数的设置是需要经验的吧,下一期会介绍其他的分割方法
有兴趣这关注微信公众号,加入我们与更多的人交流,同时也欢迎更多的来自网友的分享