基于歐式距離的分割和基于區域生長的分割本質上都是用區分鄰裡關系遠近來完成的。由于點雲資料提供了更高次元的資料,故有很多資訊可以提取獲得。歐幾裡得算法使用鄰居之間距離作為判定标準,而區域生長算法則利用了法線,曲率,顔色等資訊來判斷點雲是否應該聚成一類。
(1)歐幾裡德算法
具體的實作方法大緻是:
找到空間中某點p10,有kdTree找到離他最近的n個點,判斷這n個點到p的距離。将距離小于門檻值r的點p12,p13,p14....放在類Q裡
在 Q\p10 裡找到一點p12,重複1
在 Q\p10,p12 找到一點,重複1,找到p22,p23,p24....全部放進Q裡
當 Q 再也不能有新點加入了,則完成搜尋了
因為點雲總是連成片的,很少有什麼東西會浮在空中來區分。但是如果結合此算法可以應用很多東東。比如
半徑濾波删除離群點
采樣一緻找到桌面或者除去濾波
當然,一旦桌面被剔除,桌上的物體就自然成了一個個的浮空點雲團。就能夠直接用歐幾裡德算法進行分割了,這樣就可以提取出我們想要識别的東西
在這裡我們就可以使用提取平面,利用聚類的方法平面去掉再顯示剩下的所有聚類的結果,在這裡也就是有關注我的微信公衆号的小夥伴向我請教,說雖然都把平面和各種非平面提取出來了,但是怎麼把非平面的聚類對象可視化出來呢?
哈哈,剛開始我也以為沒有例程實作這樣的可視化,也許比較難吧,但是仔細一想,提取出來的聚類的對象都是單獨的顯示在相對與源檔案不變的位置是以我們直接相加就應該可以實作阿~是以廢話沒多說我就直接寫程式,的确可視化的結果就是我想要的結果
那麼我們看一下我的代碼吧
編譯生成可執行檔案後結果如下
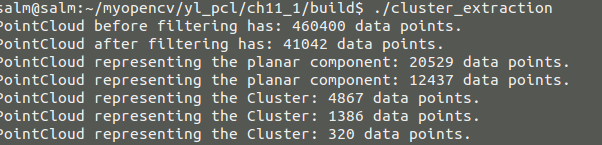
那麼我們檢視以下源檔案可視化的結果
再可視化我們聚類後除了平面的可視化的結果,從中可以看出效果還是很明顯的。
當然總結一下,我們在實際應用的過程中可能沒那麼輕松,因為我們要根據實際的點雲的大小來設定相關的參數,如果參數錯誤就不太能實作現在的效果。
是以對實際應用中參數的設定是需要經驗的吧,下一期會介紹其他的分割方法
有興趣這關注微信公衆号,加入我們與更多的人交流,同時也歡迎更多的來自網友的分享