1 海洋捕食者算法(MPA)定义
海洋捕食者算法(MPA)是一种自然启发式的优化算法,它遵循在最佳觅食策略中自然支配的规则,并且在海洋生态系统中遇到捕食者与猎物之间的速率策略。
2 海洋捕食者算法(MPA)流程
(1) 初始化精英矩阵(Elite)和猎物矩阵(Prey)
猎物矩阵(Prey) 矩阵每一个元素 Xij 的初始化方法:
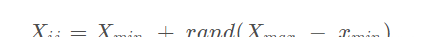
最终得到的Prey矩阵:
其中,n是种群的规模,d是每个维度的位置(问题的解的维度)。
对每一个Prey个体Xi = [Xi,1, Xi,2, …, Xi,d], 计算其适应度, 然后使用适应度最优的个体 XI 复制n份构成Elite矩阵
其中n是种群的规模,d是每个维度的位置(问题的解的维度),Elite的维度与Prey的维度相同。
(2)接着我们开始进行优化。在优化的过程中,具有三个步骤。
步骤一:
当迭代次数小于最大迭代次数的三分之一的时候
其中,RB 是采用布朗随机游走产生的随机数组成的向量,维度是 d(问题的求解规模,下同)。si 代表移动的步长。 P是一个常数,等于0.5。R是一个0到1之间的均匀分布的随机数组成的向量,维度是 d。
RB相当于一般化的高斯分布(Normal Gaussian distribution)。每一个元素 RBi 可以通过下列表达式来计算:
步骤二:
当迭代次数大于最大迭代次数的三分之一而小于其三分之二时,种群分两部分进行操作。
前半部分种群跟新规则如下:
其中, RL 是 Levy 分布组成的出来的一个向量,维度是 d。P是一个常数,等于0.5。R是一个0到1之间的均匀分布的随机数组成的向量,维度是 d。
RL 的每一项元素 RLi 可以由下列式子计算得来:
其中,C 和 α是一个常数,分别等于0.05和1.5。
在上面的表达式中
后半部分种群跟新规则如下:
这里RB 是采用布朗随机游走产生的随机数组成的向量,维度是 d。P是常数,等于0.5。CF是步长si 的自适应参数(下同), 定义为
其中, Iter是迭代次数,Max_Iter是最大迭代次数。
步骤三:
当迭代次数大于最大迭代次数的三分之二时,进入第三个阶段,此时种群更新规则如下:
(3) 解决涡流形成和FADS效应(Eddy formation and FADs’ effect)
此操作的作用是让算法在迭代过程中尽可能跳出局部最优解,已达到更好的寻优精度。
其中r是一个随机数, FADS是一个影响优化过程的常数,等于0.2。r1和r2是Prey两个随机下标, 1 ≤ r1,r2 ≤ n。 U是一个包含0和1的二进制向量,维度是d。U的每一个元素 Ui 定义为
其中random是一个0到1的随机数,FADs等于0.2。
(4) 海洋记忆(Marine memory)
这一步骤进行对Elite(精英)矩阵的更新。
针对每一个Prey矩阵中的个体Preyi ,计算其适应度,若适应度由于Elite矩阵矩阵中相应的位置的适应度时,则将该个体替代原来精英矩阵中相应的个体。然后在计算整个精英矩阵中最优个体的适应度,若符合要求,则算法结束,否则继续迭代。
算法的流程图总结出来如下:
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.