1 海洋捕食者算法(MPA)定義
海洋捕食者算法(MPA)是一種自然啟發式的優化算法,它遵循在最佳覓食政策中自然支配的規則,并且在海洋生态系統中遇到捕食者與獵物之間的速率政策。
2 海洋捕食者算法(MPA)流程
(1) 初始化精英矩陣(Elite)和獵物矩陣(Prey)
獵物矩陣(Prey) 矩陣每一個元素 Xij 的初始化方法:
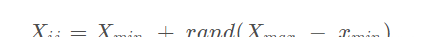
最終得到的Prey矩陣:
其中,n是種群的規模,d是每個次元的位置(問題的解的次元)。
對每一個Prey個體Xi = [Xi,1, Xi,2, …, Xi,d], 計算其适應度, 然後使用适應度最優的個體 XI 複制n份構成Elite矩陣
其中n是種群的規模,d是每個次元的位置(問題的解的次元),Elite的次元與Prey的次元相同。
(2)接着我們開始進行優化。在優化的過程中,具有三個步驟。
步驟一:
當疊代次數小于最大疊代次數的三分之一的時候
其中,RB 是采用布朗随機遊走産生的随機數組成的向量,次元是 d(問題的求解規模,下同)。si 代表移動的步長。 P是一個常數,等于0.5。R是一個0到1之間的均勻分布的随機數組成的向量,次元是 d。
RB相當于一般化的高斯分布(Normal Gaussian distribution)。每一個元素 RBi 可以通過下清單達式來計算:
步驟二:
當疊代次數大于最大疊代次數的三分之一而小于其三分之二時,種群分兩部分進行操作。
前半部分種群跟新規則如下:
其中, RL 是 Levy 分布組成的出來的一個向量,次元是 d。P是一個常數,等于0.5。R是一個0到1之間的均勻分布的随機數組成的向量,次元是 d。
RL 的每一項元素 RLi 可以由下列式子計算得來:
其中,C 和 α是一個常數,分别等于0.05和1.5。
在上面的表達式中
後半部分種群跟新規則如下:
這裡RB 是采用布朗随機遊走産生的随機數組成的向量,次元是 d。P是常數,等于0.5。CF是步長si 的自适應參數(下同), 定義為
其中, Iter是疊代次數,Max_Iter是最大疊代次數。
步驟三:
當疊代次數大于最大疊代次數的三分之二時,進入第三個階段,此時種群更新規則如下:
(3) 解決渦流形成和FADS效應(Eddy formation and FADs’ effect)
此操作的作用是讓算法在疊代過程中盡可能跳出局部最優解,已達到更好的尋優精度。
其中r是一個随機數, FADS是一個影響優化過程的常數,等于0.2。r1和r2是Prey兩個随機下标, 1 ≤ r1,r2 ≤ n。 U是一個包含0和1的二進制向量,次元是d。U的每一個元素 Ui 定義為
其中random是一個0到1的随機數,FADs等于0.2。
(4) 海洋記憶(Marine memory)
這一步驟進行對Elite(精英)矩陣的更新。
針對每一個Prey矩陣中的個體Preyi ,計算其适應度,若适應度由于Elite矩陣矩陣中相應的位置的适應度時,則将該個體替代原來精英矩陣中相應的個體。然後在計算整個精英矩陣中最優個體的适應度,若符合要求,則算法結束,否則繼續疊代。
算法的流程圖總結出來如下:
1 matlab版本
2014a
2 參考文獻
[1] 包子陽,餘繼周,楊杉.智能優化算法及其MATLAB執行個體(第2版)[M].電子工業出版社,2016.
[2]張岩,吳水根.MATLAB優化算法源代碼[M].清華大學出版社,2017.