这是菜鸡的我第一次写这类题目:
题意:就是在N*N的棋盘上,每一行,每一列,所有的对角线都只能有一个棋子。
先分析:假若N=4;
则
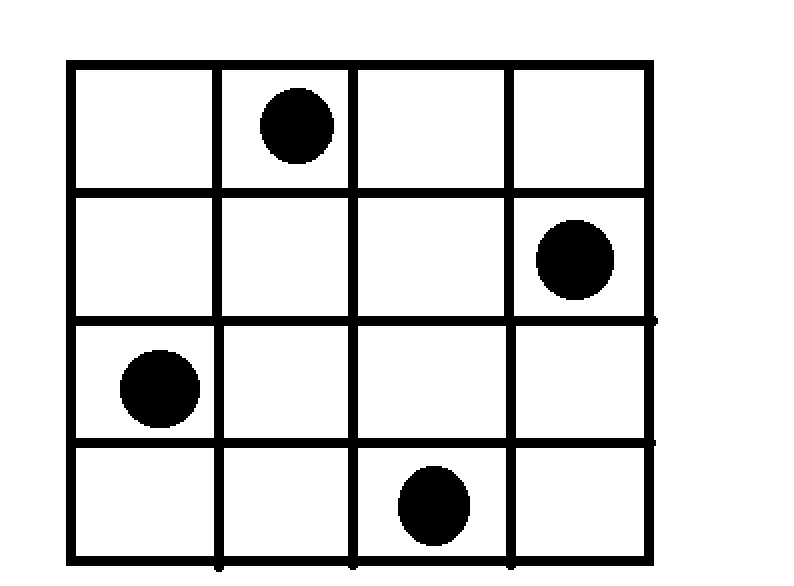
为其中的一种答案。要输出左右的解,肯定要枚举出所有的解。那么非常自然的想到递归!
根据题意,每一步棋子都满足,在一行,一列,两个对角线。那么怎么解决呢?
总体递归思路,肯定是以一行为处理单位的啦。每一行总从左到右是判断是否这个棋子可以判断。
不相邻行的两个棋子:
在这里,我们先解决不为相邻行时,两个棋子不同列不同对角线问题。
不同列:直接定义一个数组,比如b[ 1 ]=1就表示第1列已经摆了一个棋子了。那么后面的棋子直接判断就行了。
不同列:
很明显在出现这种情况之前一定会出现这种摆法:
所以根本不用担心这种情况的发生。
相邻行的两个棋子:
我们解决怎样判断同一列,在两个对角线中。
对角线一:
假设第一个点坐标为(x, y)那么,相邻行并且同对角线的下一个点的坐标是就是(x+1, y-1),对吧。是不是找到规律了。
x+y=(x+1)+(y-1) 这样就定义一个数组c[], 那么 c[x+y]=1就可以表示点(x, y)所在的这类这条对角线已经有一个棋子。
对角线二:
这类对角线的上的点的坐标变化都是横纵坐标各自加1.这其实很好办,每个坐标都满足x-y+n=k,每一条对角线对应唯一的一
个k值.至于x,y谁在前谁在后都无所谓,关键是抵消加1这个操作。那么定义d[ x-y+n ]=1表示这个对角线已经有了一个棋子。