這是菜雞的我第一次寫這類題目:
題意:就是在N*N的棋盤上,每一行,每一列,所有的對角線都隻能有一個棋子。
先分析:假若N=4;
則
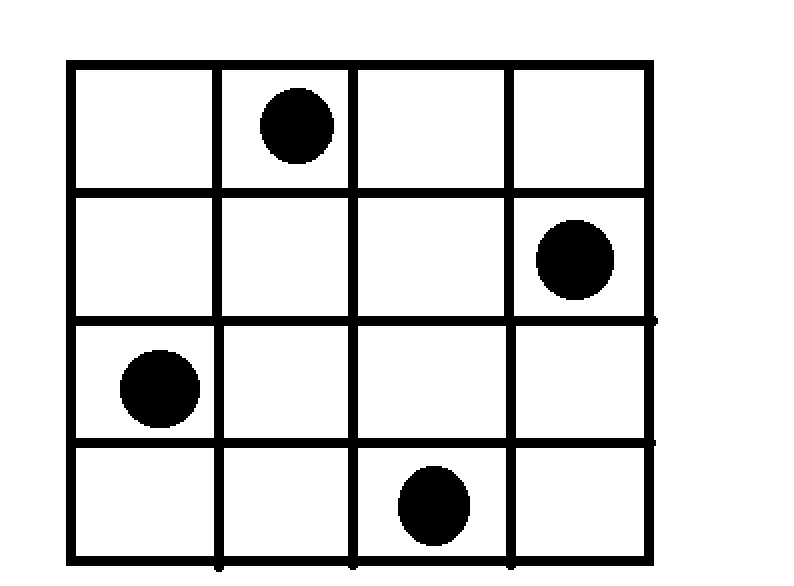
為其中的一種答案。要輸出左右的解,肯定要枚舉出所有的解。那麼非常自然的想到遞歸!
根據題意,每一步棋子都滿足,在一行,一列,兩個對角線。那麼怎麼解決呢?
總體遞歸思路,肯定是以一行為處理機關的啦。每一行總從左到右是判斷是否這個棋子可以判斷。
不相鄰行的兩個棋子:
在這裡,我們先解決不為相鄰行時,兩個棋子不同列不同對角線問題。
不同列:直接定義一個數組,比如b[ 1 ]=1就表示第1列已經擺了一個棋子了。那麼後面的棋子直接判斷就行了。
不同列:
很明顯在出現這種情況之前一定會出現這種擺法:
是以根本不用擔心這種情況的發生。
相鄰行的兩個棋子:
我們解決怎樣判斷同一列,在兩個對角線中。
對角線一:
假設第一個點坐标為(x, y)那麼,相鄰行并且同對角線的下一個點的坐标是就是(x+1, y-1),對吧。是不是找到規律了。
x+y=(x+1)+(y-1) 這樣就定義一個數組c[], 那麼 c[x+y]=1就可以表示點(x, y)所在的這類這條對角線已經有一個棋子。
對角線二:
這類對角線的上的點的坐标變化都是橫縱坐标各自加1.這其實很好辦,每個坐标都滿足x-y+n=k,每一條對角線對應唯一的一
個k值.至于x,y誰在前誰在後都無所謂,關鍵是抵消加1這個操作。那麼定義d[ x-y+n ]=1表示這個對角線已經有了一個棋子。