In this article, we will continue from my previous article to learn about the history of the Standard Model from the 1950s to the end of the 1960s. We'll cover the development of particle accelerators, the story of hadrons, and symmetry-breaking.
A brief history of the Standard Model (to 1950s), the best theory describing particles and their interactions
<h1 class="pgc-h-arrow-right" data-track="3" particle accelerators and symmetry > 1950s-1960s </h1>
Since the 1950s, the vast majority of particle physics experiments have revolved around crashing particles together. The principle is simple — it accelerates particles to nearly the speed of light and then allows them to collide. After the particles collide, analyze how they spread out to see if they match theoretical predictions. Physicists calculate scattering amplitudes to predict what scattering should look like. Scattering amplitude is a probability distribution that describes how particles may be in a state after interacting. Amplitude analysis is a compulsory course in quantum field theory.
A particle accelerator is a device that accelerates particles to the high energy required for a scattering experiment. In the 1950s, there was a significant improvement in particle accelerators and bubble chambers. In the late 1940s, physicists usually used synchrotrons to do this experiment. A synchrotron is an accelerator that accelerates particles with a magnetic field. As the particle's energy increases, so does the strength of the magnetic field to keep up with it.
The magnetic field strength needs to increase as the particles increase in velocity and keep them in a circular shape. Otherwise, the particles will deviate from the direction.
Synchrotrons were used in the late 1940s to accelerate electrons, and it is often much easier to get electrons closer to the speed of light (compared to protons). The energy required is usually around 1 GeV. Accelerating protons in synchrotrons was not successful until 1952, and further development of proton synchrotrons was able to generate energy E≥ MeV.
The 1950s was a golden decade during which dozens of particles were discovered, most of which were associated with strong interactions. These particles are mainly hadrons. A hadron is a particle made up of quarks, which is an elementary particle that we'll talk about later. Protons and neutrons are hadrons, but there are other examples, such as mesons.
Physicists didn't take the concept of quark seriously at the time. A quark is an elementary particle that is brought together by a strong interaction, and the carrier of the strong interaction force is a gluon. In quantum chromodynamics there is a theory about quarks and their interactions.
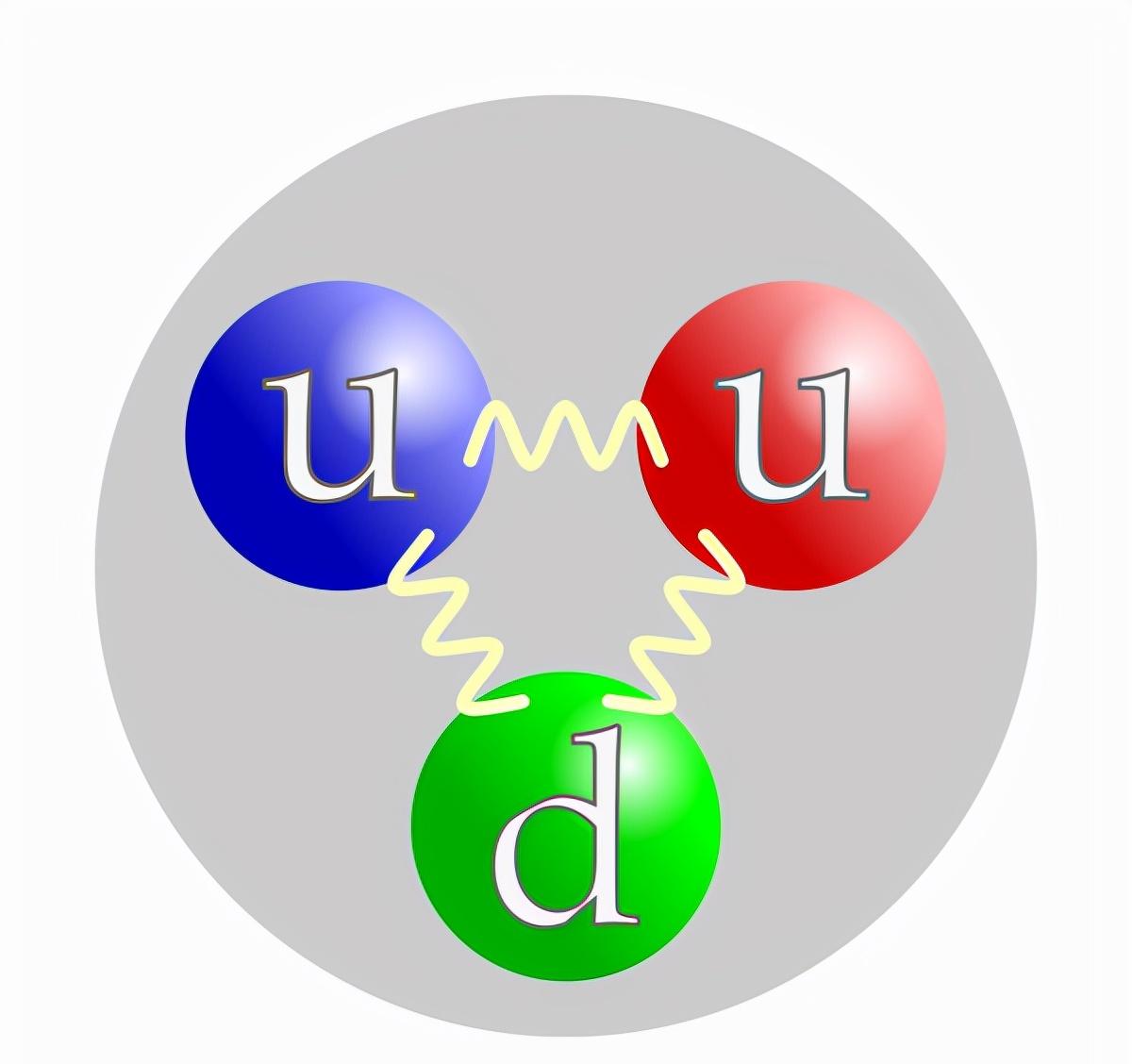
The image above is a proton. It consists of two "up" quarks and a "down" quark. The quarks are held together by strong interaction vectors, gluons.
Hadrons are divided into two different types, depending on how many quarks they are made up of. Hadrons with two quarks are called mesons, while hadrons with three quarks are called hadrons. The hadrons you might know are protons and neutrons, both of which consist of three quarks. The π meson that we discussed in the previous article is a type of meson.
Entering the world of strange atoms, why can it trigger new physics and even lead to energy breakthroughs?
There are specific types of properties associated with particles, and we usually associate these properties with particles. One of the features, charge, is something we're familiar with. Protons have a positive charge, while electrons have a negative charge. The concept of charge is important because it remains constant during the interaction.
As new particles are discovered, physicists speculate that there may be other types of charges. One of these species is strangeness, which plays a role in decay. Singularity is a charge that is conserved when objects interact under strong interactions.
In addition, there is a property known as "parity", which roughly refers to encoding the direction of particles. It turns out that unlike electromagnetic and strong interactions, parity is not conserved under weak interactions. In the experiments of Wu Jianxiong and others, it was found that the β decay of cobalt changed direction. This suggests that parity is not the fundamental symmetry of nature as once thought.
<h1 class="pgc-h-arrow-right" data-track="16" > symmetry of the 1960s </h1>
How is the symmetry of physical theory closely related to conservation quantities such as charge? Typically, a physical theory has a correlation group of symmetries. For example, in quantum electrodynamics (the theory that governs the electromagnetic force), we have a symmetrical structure that mathematicians call "U(1) symmetry", mediated by photons.
Other theories, and the resulting symmetry groups, somehow unify the weak, strong, and electromagnetic interactions. An example is the Young-Mills theory, a non-Abelian symmetry group. It is currently used in the Standard Model, but at the time, the mediating particles it predicted had not yet been discovered, so the scientific community rejected the theory.
The lack of a uniform group of symmetries is a problem. In the 1950s, so many particles were discovered, but it was not known which particles were elementary particles and which were not. However, in 1961,
The eight-part body of the meson
The octet method is a method that systematically organizes different particles according to the representation of a symmetric group called "SU(3)". A symmetry group is characterized by a set of mathematical objects that obey the basic rules of symmetry. For example, to represent a group of rotations, I can give you an angle that lets you rotate a circle between 0 and 360 degrees. In this case, I use a number to represent the rotation group. This will be a one-dimensional representation of the rotation group. However, I can also represent it with a 2×2 matrix that represents rotation, which would be a two-dimensional representation.
There is an idea to add some structure to particles by organizing them into representatives of groups. Representations of groups like SU(3) can be seen as a grid on which the X axis is one conservation quantity and the Y axis is another conservation quantity. Neutrons and protons are two states of a single polymorphism that are part of the 8-dimensional representation of SU(3). This is represented in the chart below of singularity and charge. Each of the eight dimensions predicts or agrees with the presence of particles.
There is also a 10-dimensional SU(3) notation, Ω-particle has not yet been discovered, but from the grid diagram, Gell-Mann predicted its existence and then discovered it shortly after. Then, in 1964, Gell-Mann et al. again came up with the idea of Quark. In mathematics , the symmetry group has an " intrinsic " representation , called the fundamental representation. The basic representation of SU(3) is three-dimensional, which prompted the idea of quarks, since three quarks make up a hadron. The original quarks were up, down, and odd quarks.
For mathematical reasons, the existence of 10 notations, singularity, quarks, and fermions is not possible unless there is another conservation quantity. Greenberg in 1964 and Nambu and Han proposed the concept of color in 1965 to solve this problem. In 1967, deep inelastic scattering gave the first evidence that there was something inside the protons and neutrons. Then people started taking Quark's idea seriously.
<h1 class="pgc-h-arrow-right" data-track="25" > symmetry is broken </h1>
Explain the best mechanism for particles to have mass—spontaneous symmetry breaking—how to understand negative mass?
These developments are all good, but no one can explain why particles have mass. To do this, they need additional mathematical mechanisms. Back in 1961, South, Goldstone, Salam, and Weinberg came up with the idea of symmetry breaking. The South got the idea of symmetry-breaking from superconductivity. Symmetry breaking refers to the collapse of field equations into a state under certain conditions, such as lower temperatures, that does not necessarily maintain the original symmetry of the theory itself.
Goldstone realized that when decomposing a symmetry into a smaller group of symmetries, one particle should be massless and the other massed.
That's why particles may have the mechanism behind mass, and in 1964, the Higgs mechanism was discovered. The Higgs mechanism is a symmetry-breaking model that explains the mass in the Standard Model. The Higgs mechanism also predicted the necessary existence of a new particle, the Higgs boson discovered in 2013.
Hopefully, this article has given some details about the relatively recent developments of the Standard Model. In the next article, I will write about the current problems of the Standard Model.