Legend has it that when the ancient Fuxi clan was alive, there were dragon horses that jumped out of the Yellow River with river maps on their backs; there were turtles that jumped out of Luoshui and carried Luoshu on their backs. The Fuxi clan evolved into Bagua according to the River Chart and the Book of Luo. The Book of Luo is the earliest magic square, explained in modern mathematical language, that is, to use 1 to 99 nine numbers, filled in nine grids, so that the sum of 3 numbers in each horizontal row, each vertical column, and two diagonals is equal to 15.
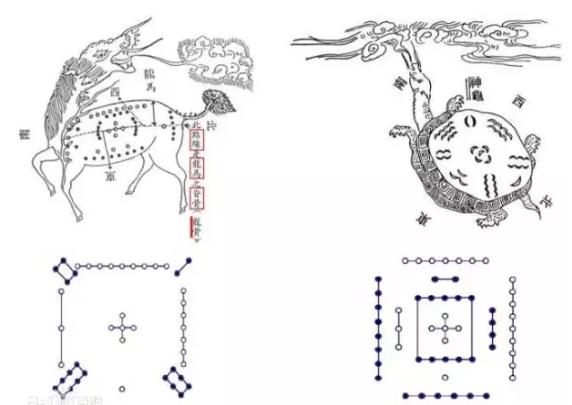
Some experts believe that the "river map" is actually the source of Fuxi's eventual creation of the Five Elements Of Gossip. The ancients also believed that the "river map" is a celestial cosmic map centered on the earth, which contains the mysteries and mysteries of heaven and earth, just as the "positioning of heaven and earth" mentioned in the "I Ching" is the same principle. If the number of the river chart is connected internally and externally, it will be found that it consists of an internal rotation map of 1-3-7-9 of the yang number, an external rotation map of 2-4-6-8 of the yin number, an odd and even number of interlaced rotations, and 5 and 10 as the core median. This constitutes the cosmic model diagram, which is the so-called innate taiji diagram.
Another legend, according to legend, when Dayu was in Luoshui, the Luoshui God Turtle dedicated a Luoshu to Dayu, which has a strange picture as shown in the picture, which is translated with today's mathematical symbols, that is, a third-order magic square, that is, 1 to 9 in the square array of 3×3, in which each row, column and two diagonal numbers are equal.
The number of yin and yang embodied in the Book of Luo is a total of forty and five, and the number of phases from 1 to 9 is the number of life and death of all things in heaven and earth. This number is listed in total, constituting a nine-star chart, according to the weekly division, the forty-five numbers are synthesized into 45 degrees of yin and yang, with the principle of the eight directions of the weekly flow, multiplied to get a number of 360 degrees, 360 degrees represents the weekly operation, harmonious and unimpeded.
Confucius said: "The river is out of the map, Luo is out of the book, and the saint is out of it." In the evolution of Heluo civilization, we see that the source of Chinese civilization is fully presented in the "I Ching", the avenue is simple, and the principle of all things derived from Heluo culture is infinite and mysterious. Later generations concluded that the information they reflected was essentially a "river map" to represent the miniature of the universe, a "Luo Book" to represent the miniature of the earth, a river map as a body, and a Luo Book as a use. Since then, the grand map of Chinese civilization has opened the prelude from that moment.
The magic square, also known as the phalanx, is also called the vertical and horizontal map. It is a traditional Chinese game. In the old days, it was more common in government offices and schools. It is characterized by arranging several numbers in a square matrix so that the sums of several numbers in the same row, the same column, and the same diagonal are equal.
The nine-palace numeral "two nine four, seven five three, six one eight", which is the basis of the third order of the Luo Shu, is clearly recorded in the ancient book "The Book of Dai Li" volume 8 "Ming Tang Chapter" published in 80 AD, which is a great creation of Chinese in mathematics, which laid the foundation for an important branch of mathematics- combinatorial science.
The earliest magic square abroad was carved on a stone plaque in front of the Jain temple in India, which is a product of the 12th-13th centuries. This is the earliest documented fourth-order magic formula. In addition to the sum of the rows, columns, and diagonals is 34, the sum of the 4 numbers within any 2×2 square is also 34. This magic square is a pan-diagonal magic square (perfect magic square). Europe did not begin to study the magic formula until the 14th century, nearly two thousand years later than our country.
Yang Hui, an outstanding mathematician of the Southern Song Dynasty, was the first to concoct various magic squares, which were recorded in his edited "Ancient Extraction Algorithm" in 1275; the eighteenth-century American scientist and inventor Franklin made the eighth-order magic square as shown in Figure 2. Its illusory sum is 260, and it has some unique properties, such as the polyline formed from 16 to 10, and then from 23 to 17∧ the sum of the eight numbers on the upper eight numbers is also 260, and the sum of the eight numbers on the ∨ of the polyline parallel to this polyline is also 260.
In 1977, the United States launched the Voyager I and Voyager II spaceships, which carried two mathematical objects, one Pythagorean and one Jaina Square, as a signal of human intelligence in an attempt to establish contact with "aliens".
This perfect magic square also has the property of adding numbers to a constant number on all "folded diagonal lines", for example, squares 2, 12, 15, 5, and squares 2, 3, 15, and 14 are all diagonal lines, and two identical magic squares can be restored side by side to restore the diagonal. Whether you move the squares of the top row of the complete magic square to the bottom or vice versa, or move one of the columns on the side to the other side, you still get a perfect magic square.
Magic squares, a wonderful blend of culture and mathematics, and how many unsolved mysteries there are! Mathematicians focus on revealing the mystery of the arrangement and combination of magic square numbers, and scientists hope that the perfect nature of the magic square will help human beings realize the dream of communicating with alien civilizations, perhaps the code of communication with alien civilizations. Artists strive to integrate the magic square pattern into the artistic design, and the philosopher looks forward to the easy-to-learn ideas contained in the magic square.
The Hundred Sons of Macao's Return to the Motherland is a ten-order magic square formed by 1, 2, 3,......,100. At the top of Zhuhai Yingbin Avenue Banbanshan Mountain, you can intuitively view the Gongbei Port Building, and behind the building is Macau. Enter the gate of Banzhangshan Park for about 100 meters, and there is a winding stone ladder on the right side, 1999 steps to reach the summit. At the top, looking in the direction of Macao, a large stone stele can be seen called "The Hundred Sons of Macao's Return to the Motherland". The central four numbers read consecutively "1999.12.20", marking the day of Macao's return to the motherland. The two numbers "23 50" in the middle of the last row indicate the area of Macau.
Example 1. Using the integral accounting method, it can be proved that the third-order magic formula has the following properties:
(1) In the third-order magic square, the sum of the three numbers in each row, each column, and each diagonal line is equal to 1/3 of the sum of these nine numbers;
(2) The sum of the three numbers in each row, each column, and each diagonal in the third-order magic square is 3 times the number of central cells;
(3) The number of central squares of the third order magic square is the average of nine numbers;
The holistic accounting method regards some objects in the problem as a whole, observes and analyzes the overall characteristics and structure between the problem and the conclusion in the problem, and calculates and reasons from the whole.
(4) In the third-order magic square, each number is added or multiplied by an identical number, and the resulting graph is still the third-order magic square.
Analysis: Some problems involve more quantities, complex relationships, we need to introduce different letters, easy to express the quantity relationship, in the solution we do not need (or can not) find out the value of all letters, only the value of the key letters.
As shown in the figure is a third-order magic square, and the sum of three numbers per row, each column, and each diagonal line is S, in order to fully represent the equivalence relationship, it is necessary to set multiple unknowns, set but not seek, and use the overall accounting method to prove.
In the above proof process, 9 unknowns are introduced for reasoning, and the problem is solved by overall deformation and substitution. The nature of the third-order magic square is an important basis for the construction of the magic square, which answers the question of "how the third-order magic square is constructed" from one side.
Example 2. As shown in Figure (1), a, b, c, d, e, f, g, h, i represent a number in 1, 2, 3, 4, 5, 6, 7, 8, 9, respectively, different letters represent different numbers, so that the sum of the 3 numbers in each small circle is equal, so what is the value of a + d + g?
Analysis: Let this equal sum be S, now sum the 27 numbers in these 9 small circles (3×9 =), and you can get:
9s=(1+2+...+9)+2×(a+b+c+d+e+f+g+h+i)=3×(1
+2+…+9)=3×45=135,故S=15.
First from the small circle where 9 is located, h is at least 1, i can only be 5 at most, and then from the small circle where 1 is located, a can only be 9 at most, because 1 + i + a = 15, so it must be i = 5, a = 9, from which you can get the figure (2).
Comparing the positions of each number in Figure (1) and Figure (2), we can see that a+ d + g = 9 + 3 + 6 = 18.
Of course there can also be another solution.
Sum 18 numbers in 6 small circles (3×6=) containing 1, 2, 4, 5, 7 and 8, and we will obtain:
6×15=1+2+4+5+7+8+(a+b+c+d+e+f+g+h+i)+a
+d+g,即90=72+a+d+g,所以a+d+g=90-72=18.
Example 3. Fill in the numbers 1, 2, 3..., and 9 in the 9 circles in the figure, and require that the sum of the numbers in the three circles on each side of △ABC and △DEF is equal to 18.
(1) Give a filling method that meets the requirements;
(2) How many different filling methods are there? Prove your conclusions. (Shandong Provincial Competition Questions)
Analysis: Let the sum of the three numbers A, B, and C be x, the sum of the three numbers of D, E, and F is y, and the sum of the remaining three numbers is z, then x +y+z=1+2+...+9=45(1),
From the sum of the numbers of the three circles in the six edges in the figure is 18, 2 + 3y + 2x = 6× 18 = 108 (2), from (2) - (1) to x + 2y = 108 -45 = 63 (3),
Add the sum of the numbers of the three circles on each side of AB, BC, and CA to get 2x + y= 3× 18 = 54(4),
Syndic (3), (4) solve x =15, y =24, and then z=6.
In 1 to 9, the sum of the three numbers is only 7, 8, 9, so in the D, E, F three circles, only 7, 8, 9 three numbers, a total of 6 different fillers. Obviously, once the number of these three circles is determined, according to the requirements of the question, the number of the remaining six circles is also determined, and the conclusion is obtained, there are 6 different ways to fill in.
With the full exploitation of the properties of the magic square and the development of combinatorial mathematics, the magic square has a wide range of applications in arts and crafts design, combinatorial analysis, artificial intelligence, graph theory, password editing, image security processing and so on.
(1) As shown in the figure, the numbers in each row and column in the figure are composed into a three-digit number, and their inverse ordinal numbers are written, and the following wonderful calculations can be obtained:
(2) As shown in the figure, the earliest European magic square appeared in the copperplate engraving "Melancholy" made by the German painter Dürer (1471-1528) in 1514.
In 1514, the German painter Dürer created a steel engraving of "Melancholy", which hung a 4th-order magic square in the upper right of the picture, which reflected the deep "sadness" of people who did not have sufficient knowledge and wisdom to explore the mysteries of nature.
Through the conversion of numbers and shapes, the above magic square can also be applied to art design.
The most dramatic way to demonstrate the magic properties of this magic square is the one described in a 1938 paper by two mathematicians J. Barkley Rosser and Robert J. Walker at Cornell University. First join the top and bottom of this completely illusory square together to form a cylinder, and then stretch it. Rounded curved surface twisted into a tire shape. All rows, columns, and diagonals are now closed. If we start with either square and move two diagonally, we will always reach the same square. The closed circle of each four squares, whether directly or obliquely added, and the sum is 34, like any four-block group in any magic square.
Because of the unpredictable and profound magic, it not only attracts ordinary mathematics enthusiasts, but also attracts many mathematicians. The famous American magic master M. Gardner (1914~) in addition to careful study, but also put forward his own questions - is there an anti-illusion party? If you fill in the nine numbers of 1, 2、...、 3、...、9 into these nine boxes, will it appear that the sum of the numbers in any row, column, or diagonal is not equal? It seems that the research path of the magic square is still very long, and people need to constantly explore it.
In modern times, it has been found that magic squares are closely related to combinatorial analysis, and it has certain uses in countermeasure theory, graph theory, artificial intelligence, programming, etc. In the past, it was purely a mathematical game, and it was gradually discovered that it contained many profound mathematical principles and applied it to many occasions. The rapid development of electronic computer technology has injected fresh blood into this ancient theme. Mathematicians delved further into it, finally making it an extremely rich new branch of mathematics— combinatorial mathematics.