傳說,古撫玄的時候,有龍馬從黃河裡跳出來,背上背着河圖;傅氏根據河流地圖和書籍演變成八卦。洛書是最早的魔方,用現代數學語言解釋,就是用1到99個數字,填上九個網格,使每行、每一垂直列和兩個對角線三個數字的總和等于15。
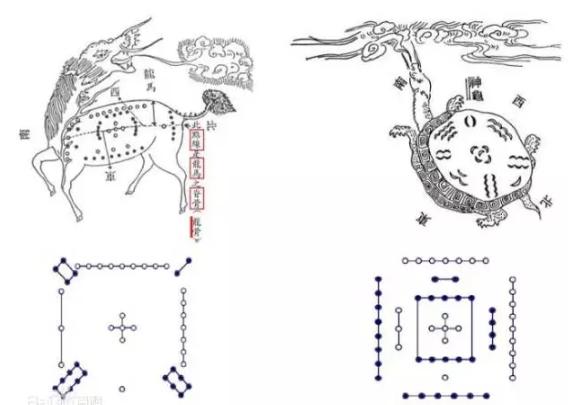
有專家認為,"河圖"是傅琦最終造就的五行八卦的來源。古人還認為,"河圖"是以地球為中心的天體宇宙圖,有着隐秘和奧秘,正如《易經》中提到的"世界與地球定位",也是同樣的原因。如果你對河圖的數量進行内部外交聯系,你會發現它由陽數的1-3-7-9的内部旋轉圖組成,外向圖由負數2-4-6-8組成,奇數和偶數交錯旋轉,5和10是核心中位數。這構成了宇宙的模型圖,即所謂的先天太極圖。
另一個傳說是,根據傳說,當水獺在水中時,Lo水龜獻給大冢一本書,其中有一幅奇怪的圖檔,用今天的數學符号翻譯,是一個三階魔方,即在3×3的正方形中填入1到9, 其中每行、每列和兩個對角線數字相等。
羅蜀所展現的陰陽總數為四十五,天地數按1~9相的順序排列,是天地萬物的生死數。這個數字一共列在九星圖中,構成一張九星圖,按周長、45個合成陰陽45度的數,以八邊的周流,乘以360度的數,代表360度,代表每周操作,圓融無阻。
孔子:"河出地圖,羅出書,聖人就是。在海洛文明的演進中,我們看到中華文明的源泉在《簡易書》中完整地呈現,簡之路,海洛文化源于萬物大理,無與倫。後來人們得出結論,他們所反映的資訊,實質上是"河圖"來代表宇宙的微觀世界,用"loshu"來代表地球的縮影,把河圖當作身體,把書當成一個用途,把機會分割開來,這就是長篇大論的終結。從此,中華文明的宏偉地圖,從那一刻拉開了序幕。
幻象方塊,又稱方陣,又稱水準圖。這是一個傳統的中國遊戲。在過去,它在政府辦公室和學校中最為常見。它的特點是将幾個數字排列成正方形,以便同一行,列和對角線中幾個數字的總和相等。
九門數字"294,753,618"是羅蜀三階魔方的基礎,在古籍《戴大裡》第8卷《明堂》中都有明确記載,這是中國數學的偉大創造,奠定了數學組合重要分支的基礎。
國外最早的幻覺是在印度耆那教寺廟前的石匾上雕刻的,這是12-13世紀的産物。這是最早記錄的四階魔方。除了行、列之外,對角線和是34,它是4個數字内的平方中任意2×2,也是34。這個魔方是一個泛對角線魔方(完美魔方)。歐洲直到14世紀才開始研究幻覺,比我國晚了近兩千年。
南宋著名數學家楊輝首先炮制了各種幻覺,記載于1275年他編輯的《繼續古揀選算法》中;富蘭克林是18世紀的美國科學家和發明家,他制作了圖2所示的八階魔方。它的錯覺是260,它有一些獨特的屬性,比如從16到10,然後從23到17變成一條線∧線上的八個數字之和也是260,而平行于線的線∨八個數字的總和也是260。
金庸先生的武俠小說《射殺英雄》更是喜歡這種幻覺;1977年,美國發射了旅行者一号和旅行者2号宇宙飛船,它們上傳了兩個數學物體,一個是多個鈎子,另一個是耆那教廣場,作為人類智能的信号,試圖與外星人聯系。
這個完美的魔方還具有将常數加起來到所有"折疊對角線"的特征,例如,正方形2,12,15,5和正方形2,3,15和14是它們的對角線,您可以通過并排放置兩個相同的魔方來恢複對角線。無論您是将完全幻覺正方形的頂行的正方形移動到底部還是相反,或者将邊緣的列移動到另一側,結果仍然是一個完美的魔方。
魔方,文化與數學的奇妙融合,多少未解之謎!數學家們正試圖揭示魔方數組合的奧秘,科學家們希望魔方的完美本質能夠幫助人類實作與外星文明,或許與外星文明交流的夢想。藝術家試圖将魔方圖案融入到藝術設計中,哲學家則期待魔方中蘊含的易學思想。
澳門回程地圖是由1,230,,......,100組成的十階魔方。在珠海迎新大道的頂部,您可以直覺地拱起北港大廈,後面是澳門。進入盤長山公園大門約100米處,右側有一個非常不同的石梯可以到達山頂。在城市的頂部,望向澳門的方向,大型石碑的一側被命名為"澳門回歸百童地圖"。中央委員會連續宣讀"1999-12-20",以紀念澳門回歸之日。最後一行中間的第二個數字"23 50"表示澳門地區。
示例 1.使用整個會計方法可以證明三階魔術方具有以下屬性:
(1)在三階魔方中,每行、列和對角線的三個數字之和等于這九個數字之和的1/3;
(2)三階魔方中每行、列和對角線中三個數字之和是中心方塊數的三倍;
(3)三階中心方塊數為9的平均值;
整體算計方法把問題中的一些對象作為一個整體來看待,觀察和分析問題與問題中結論之間的總體特征和結構,從整體上進行計算和推理。
(4)在三階魔方中,每個數字相加或乘以相同的數字,得到的圖形仍然是三階魔方。
分析:有些問題涉及的數量較多,關系複雜,我們需要引入不同的字母,容易表達定量關系,在解決問題時我們不需要(或不能)找出所有字母的值,隻有關鍵字母的值。
圖為三階魔方,每行、每列、各對角線三個數的總和為S,為了充分表示等價關系,需要設定一些未知數,設定時無需求值,運用整體核算方法進行證明。
在上述證明過程中,為了推理和引入9個未知數,設定而不求,通過整體變形,替換和解決問題。三階魔方的性質是建構魔方的重要依據,從一面回答了"三階魔方是如何構造的"的問題。
示例 2.如圖(1)所示,a、b、c、d、e、f、g、h、i代表1、2、3、4、5、6、7、8、9,不同的字母代表不同的數字,是以每個小圓圈中3個數字之和相等,那麼a加d加g的值是多少呢?
分析:設定這個相等和是S,現在這9個小圓(3×9)27個數字總和,可以得到:
9s=(1+2+...+9)+2×(a+b+c+d+e+f+g+h+i)=3×(1
3×45,135,是以S.15。
首先從小圓圈開始,其中9是,h至少是1,i最多隻能是5,然後從1是的小圓圈開始,a最多隻能是9,因為1 s i s a s 15,是以必須i s 5,a s 9,這樣才能找到圖(2)。
比較圖(1)和(2)中數字的位置,您可以看到數字在圖(1)和圖2中的位置,并且可以看到a-d-g-9-3-6-18。
當然,還有另一種解決方案。
得到6個小圓圈(3×6)中的18個數字的總和,其中包含1,包括2,4,5,7和8:
6×15=1+2+4+5+7+8+(a+b+c+d+e+f+g+h+i)+a
也就是說,90, 72, a, d, g, 是以 a-d-g,90-72,18。
示例 3.将數字 1、2、3...、9 填充到圖中的 9 個圓圈中,并要求 ABC 和 DEF 每側的三個圓圈之和等于 18。
(1)給出符合要求的灌裝方法;
(2)有多少種不同的灌裝方式?證明你的結論。(山東省比賽問題)
分析:設定A、B、C三個數字之和為x、D、E、F 三個數字之和為y,其餘三個數字之和為z,則三個數字之和為z,則x-y-z-1加-2-...-9-45(1),
通過圖中的六條邊,每邊的三個圓的總和為18,三個圓的總和為2 x 3y x 2x x 6 ×18 x 108(2),乘以(2)-(1)x x 2y x 108-45 x 63(3),
将 AB、BC、CA 兩側三圈數的總和相加,得到 2x-y-3×18-54 (4),
并集 (3)、(4) 解 x x x 15、y、24,然後 z - 6。
1 到 9 中的三個數字中隻有 7,8,9 是 24,是以隻有 7,8,9 可以在 D、E 和 F 的三個圓圈中填充,總共有 6 個不同的填充。顯然,一旦确定了這三圈的次數,剩下的六圈的次數就是根據标題的要求确定的,總共得出了六種不同的填充方法。
随着幻象方塊性質群組合數學的發展,魔方廣泛應用于工藝美術設計、組合分析、人工智能、圖論、密碼編輯、圖像安全處理等。
(1)如圖所示,圖中每行、每列的編号由三位數字組成,并寫出它們的逆數,這樣可以得到以下精彩的計算:
(2)如圖所示,歐洲最早的幻覺出現在德國畫家迪勒(1471-1528)1514年的青銅版畫"蕭條"中。
1514年,德國畫家迪勒創作了一幅鋼版畫《抑郁症》,畫面右上角挂着一個四階魔方,反映了人們沒有足夠的知識和智慧去探索自然奧秘的深深"悲傷"。
通過數字和形狀的轉換,上述魔力也可以應用于藝術設計。
展示這種神奇特征的最戲劇性的方式是康奈爾大學兩位數科學家J. Barkley Rosser和Robert J. Walker在1938年的一篇論文中描述的那種。首先将這個完全幻影的正方形的頂部和底部連接配接在一起形成一個圓柱體,然後拉伸它。扭曲成類似輪胎的圓形表面。所有行、列和對角線現在都已關閉。如果我們從任一方塊開始,然後沿對角線移動兩個,我們将始終到達同一個正方形。每個四塊閉合的圓,無論是直的還是斜的,都是34,就像任何魔方中的四塊一樣。
由于各種方塊的變幻莫測和奇迹,它不僅吸引了普通的數學家,也吸引了許多數學家。除了深入研究之外,美國著名的幻影大師馬丁·加德納(Martin Gardner,1914-)還問了他自己的問題——有沒有反幻覺的一面?如果您随意填寫這九個網格1,2,3、...、99,那麼行,列或對角線中的數字之和是否微不足道?看來魔方的研究路還很長,需要人們不斷探索。
現代發現表明,魔方與組合分析之間存在密切的關系,在對策理論、圖論、人工智能、程式設計等方面都有一定的用途。過去純粹是一個虛幻的數學遊戲,它逐漸被發現包含了許多深刻的數學原理,并在許多場合得到應用。計算機技術的飛速發展,為這個古老的題材注入了新鮮血液。數學家們深入研究了它,最終使它成為數學中一個非常豐富的新分支,即組合數學。