For centuries, the Golden Ratio has been hailed as the most beautiful proportion in art and architecture. From the Parthenon to Salvador Dali's The Last Supper Sacrament, the golden ratio has been found lurking in some of the world's most famous works.
Expressed by the Greek letter phi (φ), the golden ratio is an irrational value:

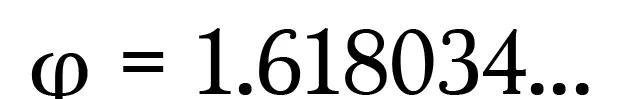
Euclid and the Golden Ratio
In Volume 6 of The Elements, Euclid gives us a definition of the Golden Ratio.
He instructs us to take a segment and divide it into two smaller segments so that the ratio of the entire segment (a+b) to segment a is the same as the ratio of segment a to segment b, as follows:
or
Golden rectangle
The golden ratio is most commonly expressed as a golden rectangle, a rectangle with a side-length ratio of 1.618:1.
The golden rectangle also has a property, if you cut out a square, you will get another golden rectangle.
Solve the golden ratio
To find the value 1.618034... Of the sources, we have to solve for proportions. For simplicity, suppose b=1 and a=x so that you can solve for x.
Step 1
Take the cross
Step 2
Subtract x+1 to set the equation to zero.
We now have a standard quadratic equation where a= 1, b = -1, and c = -1.
Step 3
Substitute these values into a quadratic formula and solve for them.
Get the solution
For better measurement, insert a=1.618 and b=1 to confirm that the proportions hold.
Now we can use itself to write the Golden Ratio!
Or equivalently,
Replace the φ in the denominator with φ =1 + 1/φ.
Let's do it again!
The golden ratio can be written as an infinite number of consecutive scores.
Look for Fibonacci
We can use consecutive fractions to approximate the golden ratio and discover interesting relationships with Fibonacci sequences.
First, we will change our consecutive score slightly.
Instead of writing a formula nested within itself, we will add subscripts to indicate that the next value (φ_n+1) can be generated from the previous value (φ_n).
Since this is an infinitely consecutive fraction, as n increases, the approximation is closer to the true value of φ.
Define φ_0 = 1. Φ_1 insert n=0.
Repeat the process to find φ_2 for n=1 because φ_2 = φ_1+1. Use the result of step 2 for φ_1.
Step 4
Continue to repeat this process.
Step 5
Check this out. There is a Fibonacci sequence! Each approximation is the ratio of two adjacent Fibonacci numbers. We no longer need the trouble of inserting values into even fractions, we can simply divide the contiguous terms of a Fibonacci sequence. We no longer need the trouble of inserting values into even fractions, we can simply divide the contiguous terms of a Fibonacci sequence.
As each calculation progresses, we find that our approximation of the golden ratio is getting closer and closer to its true value.
In fact, the limit of F(n+1)/F(n) is n → ∞ (where F(n) and F(n+1) represent the nth and n plus 1 terms in the Fibonacci sequence) converge to φ.
Visually, we can see how the Fibonacci sequence generates rectangles that are getting closer and closer to the coveted golden rectangle.
While the design community may be debating whether the golden ratio is folklore, I can say with certainty that the golden ratio is very interesting mathematically.
Classmates, have you learned to "waste"? [Proud]