本節書摘來自華章出版社《資料結構與算法 c語言版》一 書中的第3章,第3.3節,作者:徐鳳生,更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視。
棧還有一個重要應用是在程式設計語言中實作遞歸。一個直接調用自己或通過一系列的調用語句間接調用自己的函數,稱為遞歸函數。其中直接調用自己的函數稱為直接遞歸。間接調用自己的函數稱為間接遞歸。
遞歸是算法設計中最重要的手段。它通常把一個大型的複雜問題轉化為一個與原問題相似的規模較小的問題來求解。下面是常見的使用遞歸的三種情況。
(1)定義是遞歸的
現實中,有許多定義是遞歸定義的,以n!為例來說明,其定義如下:
fact(n)=1n=0//遞歸終止條件
n*fact(n-1)n>0//遞歸步驟
其遞歸算法如下:
int fact(int n){
if(n==0)return 1;
else return(n*fact(n-1));
}
(2)資料結構是遞歸的
某些資料結構就是遞歸的,則它們的操作可遞歸地描述。例如,單連結清單就是一種遞歸的資料結構,單連結清單的結點lnode的定義由data和next組成;而指針next則由lnode定義。
對于遞歸定義的資料結構,采用遞歸的方法編寫算法十分友善。例如,使用遞歸查找非空不帶頭結點單連結清單中的最後一個結點的算法可描述如下:
void findlastelem(linklist l){
if(l->next==null)printf(l->data);
else findlastelem(l->next);
(3)問題的解法是遞歸的
某些問題本身沒有明顯的遞歸結構,但也用遞歸來求,甚至有些問題隻能用遞歸求解。一個典型的例子就是hanoi塔問題。
在用進階語言編寫的程式中,調用函數和被調用函數之間的連結和資訊交換需通過棧來進行。
通常,當在一個函數的運作期間調用另一個函數時,在運作該被調用函數之前,系統需先完成三項任務:1)将所有的實參、傳回位址等資訊傳遞給被調用函數儲存;2)為被調用函數的局部變量配置設定存儲區;3)将控制轉移到被調用函數的入口。而從被調用函數傳回調用函數之前,系統也應完成下列三項任務:1)儲存被調用函數的計算結果;2)釋放被調用函數的資料區;3)依照被調用函數儲存的傳回位址将控制轉移到調用函數。當有多個函數構成嵌套調用時,按照“後調用先傳回”的原則,上述函數之間的資訊傳遞和控制轉移必須通過棧來實作,即系統将整個程式運作時所需的資料空間安排在一個棧中,每當調用一個函數時,就為它在棧頂配置設定一個存儲區;每當從一個函數退出時,就釋放它的存儲區,則目前正運作的函數的資料區必在棧頂。
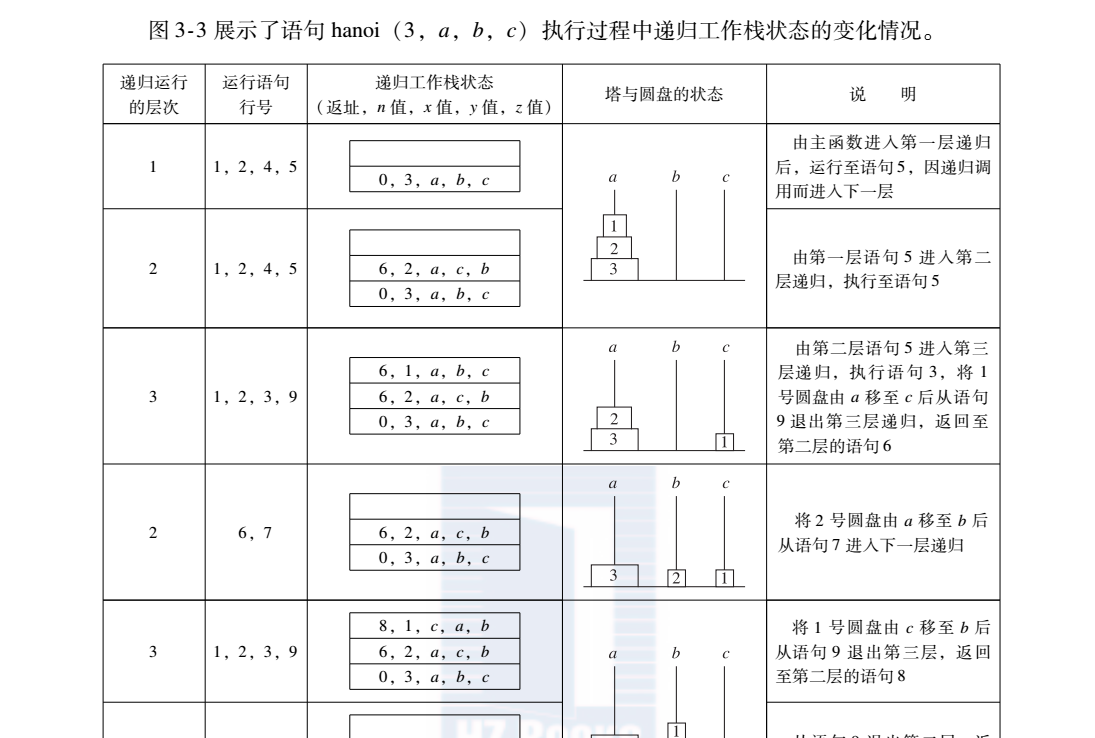
假設調用該遞歸函數的主函數為第0層,則從主函數調用遞歸函數為進入第1層;從第i層遞歸調用本函數為進入下一層,即第i+1層。反之,退出第i層傳回至上一層,即第i-1層。為了保證遞歸函數正确執行,系統需要一個“遞歸工作棧”作為整個遞歸函數運作期間使用的資料存儲區。每一層所需資訊構成一個“工作記錄”,其中包括所有的實參、所有的局部變量以及上一層的傳回位址。每進入一層遞歸,就産生一個新的工作記錄壓入棧頂。每退出一層遞歸,就從棧頂彈出一個工作記錄,則目前執行層的工作記錄必是遞歸工作棧棧頂的工作記錄,稱這個工作記錄為“活動記錄”,并稱訓示活動記錄的棧頂指針為“目前環境指針”。
下面以漢諾(hanoi)塔問題來說明遞歸的實作。
假設有三個分别命名為x、y和z的塔座,在塔座x上插有n個直徑大小不同、依次從小到大編号為1,2,…,n的圓盤。現要求将x軸上的n個圓盤移至塔座z上并仍按同樣順序疊排。移動過程中一次隻能移動一個圓盤,不允許大圓盤放在小圓盤上面,而隻能借助于中間的塔座。
如何實作移動圓盤的操作呢?當n=1時,隻要将編号為1的圓盤直接從x移至z上即可;當n>1時,可以先将編号為n的圓盤之上的n-1個圓盤借助于z移至y上,再把編号為n的圓盤移至z上,最後再将y上的n-1個圓盤借助x移至z上。顯然,這個過程是遞歸的。其遞歸算法如下:
void hanoi(int n,char x,char y,char z) //将塔座x上按直徑由小到大且自上而下編号為1至n的n個
//圓盤按規則搬到塔座z上,y可用作輔助塔座
1{
2if(n==1)
3move(x,1,z);//将編号為1的圓盤從x移到z
4else{
5hanoi(n-1,x,z,y);//将x上編号為1至n-1的圓盤移到y,z作輔助塔
6move(x,n,z);//将編号為n的圓盤從x移到z
7hanoi(n-1,y,x,z);//将y上編号為1至n-1的圓盤移到z,x作輔助塔
8}
9}
其中move定義如下:
void move(char x,int n,char z){
printf("%d号圓盤:%c---->%c\n",n,x,z);
當序列1,2,…,n依次入棧,請問如何求出其所有可能的出棧序列?下面給出求所有出棧序列的遞歸算法的描述及算法:
1)若n=1,則寫下唯一的出棧序列。
2)否則,遞歸調用該算法求出第一個元素1作為第k個元素的所有出棧序列(k=1,2,…,n)。
求所有出棧序列的遞歸求解算法如下:
int count=0;//記錄出棧序列數
char a[7],b[10000][7];//數組a存儲輸入序列(為了實作簡單,這裡假定每個元素是一位整數或一個字
//符),數組b存儲得到的所有出棧序列
void perm(char a[],int k,int n){//k為數組a中的第一個元素的下标,n為數組a中的最後一個元素的下标
int i,j,s,flag;
char temp,t[7];
strcpy(t,a);
if(k==n){
s=0; flag=0;
while((!flag)&&(strcmp(b[s],"\\ 0")))if(!strcmp(a,b[s++]))flag=1; //檢驗是否與已有出棧
//序列重複。若不重複,
//則輸出出棧序列
if(!flag){strcpy(b[s],a);count++;printf("%d:%s\\n",count,a);}
else
for(i=k;i<=n;i++){//依次求出第一個元素在第k位的所有出棧序列
strcpy(a,t);temp=a[k];
for(j=k;ja[i]=temp;
perm(a,k,i-1);
perm(a,i+1,n);
335遞歸的消除
通過上面的例子可以看出,遞歸既是強有力的數學方法,也是程式設計中一個很有用的工具。其特點是對遞歸問題描述簡潔,結構清晰,程式的正确性容易證明。然而,有時需考慮怎樣将一個遞歸算法換成等價的非遞歸算法,這稱為“遞歸消除”。研究遞歸消除的主要原因有以下兩個方面:第一,遞歸消除有利于提高算法的時空性能。在一般情況下,遞歸算法的時空性能相對較差,而非遞歸算法的時空性能要高得多。第二,研究遞歸消除有助于透徹了解遞歸機制,而這種了解是熟練掌握遞歸程式設計技能的必要前提。
根據是否需要引入工作棧作為控制機構,可将遞歸消除技術分成兩類,下面分别加以讨論。
1簡單遞歸消除(尾遞歸和單向遞歸消除)
簡單遞歸是尾遞歸和單向遞歸。其中,尾遞歸是指遞歸調用語句隻有一個,而且是處于算法的最後;單向遞歸是指遞歸函數中雖然有一處以上的遞歸調用語句,但各次遞歸調用語句的參數隻和主調用函數有關,這些遞歸調用語句互相之間參數無關,并且這些遞歸調用語句也和尾遞歸一樣處于算法的最後。這類遞歸算法可以不使用工作棧作為控制機構而直接轉換成循環算法。
尾遞歸的一個典型例子是計算階乘n!的遞歸算法,将其轉換成非遞歸算法如下:
int y=1;//計算0!
for(int i=1;i<=n;i++)//依次計算1!,…,n!
y=yi;//i!=(i―1)!i
return y;
單向遞歸的一個典型例子是計算斐波那契數列。斐波那契數列是指:數列中的每一項都等于前兩項之和,它的前幾項為1,1,2,3,5等。其遞歸算法fib(n)如下:
fib(int n){
if(n==0||n==1)return n;//遞歸出口
else return fib(n-1)+fib(n-2);//遞歸調用
将其轉換成非遞歸算法如下:
int fib(int n){
int x,y,z;
if(n==0||n==1)return n;//計算fib(0)、fib(1)
else{
int x=0,y=1,z;//x=fib(0),y=fib(1)
for ( i=2;i<= n; i++){
z=y;//z=fib(i-1)
y=x+y;//y=fib(i-1)+fib(i-2),求fib(i)形成第i項
x=z
};//x=fib(i-1)
2基于棧的遞歸消除
在複雜情況下,一個遞歸算法無法直接轉換成循環算法。例如,前面介紹的漢諾塔問題。在這種情況下,通常通過引入一個工作棧儲存“傳回位置”以實作過程調用的傳回。基于棧消除遞歸必須遵循以下規則:
1)在過程(或函數)的開始部分,插入聲明為棧的代碼并将其初始化為空,在一般情況下,這個棧用來存放參數、局部變量和函數的值,每次遞歸調用的傳回位址也要存入棧。
2)将标号l1附于第一條可執行語句。然後,對于每一處遞歸調用用一組執行規則3)~規則7)的指令來代替。
3)将所有參數和局部變量的值存入棧,棧頂指針可作為一個全程變量來看待。
4)建立第i個新标号li,并将i存入棧,這個标号的i值将用來計算傳回位址。此标号放在規則 7 所描述的程式段中。
5)計算這次調用的各實參(它們可能是表達式)的值,并把這些值賦給相應的形參。
6)插入一條無條件轉移語句轉向過程(或函數)的開始部分。
7)如果這個過程是函數,則對于這個遞歸過程中含有此次函數調用的那條語句作如下處理:對該語句的此次函數調用部分用從棧頂取回該函數值的代碼代替,其餘部分的代碼按原描述方式照抄,并将規則4)中建立的标号附于這條語句。如果此過程不是函數,則将規則4)中建立的标号附在規則6)所産生的轉移語句後面的那條語句。
以上規則是為了消除過程中的多處遞歸調用,現在對遞歸過程中出現的return進行處理(純過程結束的地方可看成是一條沒有值與其相聯系的return語句),在每個return語句的地方,執行下述規則:
8)如果棧為空,則執行正常傳回,否則執行規則9)。
9)将所有輸出參數的目前值賦給棧頂上的那些對應變量。
10)如果棧中有傳回位址标号的下标,就插入一條此下标從棧中退出的代碼,并把這個下标值賦給一個未使用的變量。
11)從棧中退出所有局部變量和參數的值,并把它們賦給對應的變量。
12)如果這個過程是函數,則插入用來計算緊接在return後面的表達式的指令,并将結果值存入棧頂。
13)用傳回位址标号的下标實作對該标号語句的轉向。
在一般情況下,使用上述規則都可将一個直接遞歸過程正确地翻譯成與之等價的非遞歸過程。下面考察一個遞歸轉化的例子。求數組a[n]中最大的元素,其遞歸算法描述如下:
int max1(int i)
{//函數傳回a[n]中最大元素的下标,其中a[n]和n均為全局變量
int j,k;
if(ij=max(i+1);
if(a[i]>a[j])k=i;
else k=j;
else k=n-1;
return k;
利用上述規則将其轉化為非遞歸算法如下:
int max2(int i){
int j,k,addr;
sqstack s;
initstack(s);//規則1),構造一個順序棧
l1:if(i{ push(s,2);//規則4)
push(s,i);//規則3)
i++;//規則5)
goto l1;//規則6)
}//if
l2:pop(s,j);//規則7)
if(stackempty(s))return k;//規則8)
pop(s,addr);//規則10)
pop(s,i);//規則11)
push(s,k);//規則12)
if(addr==2)goto l2;//規則13)
}//else
需要說明的是,不必在任何情況下都完全照搬前面的13條規則,而要具體問題具體分析。