一、AVL樹
AVL樹是一棵自平衡的二叉搜尋樹。
1、平衡因子
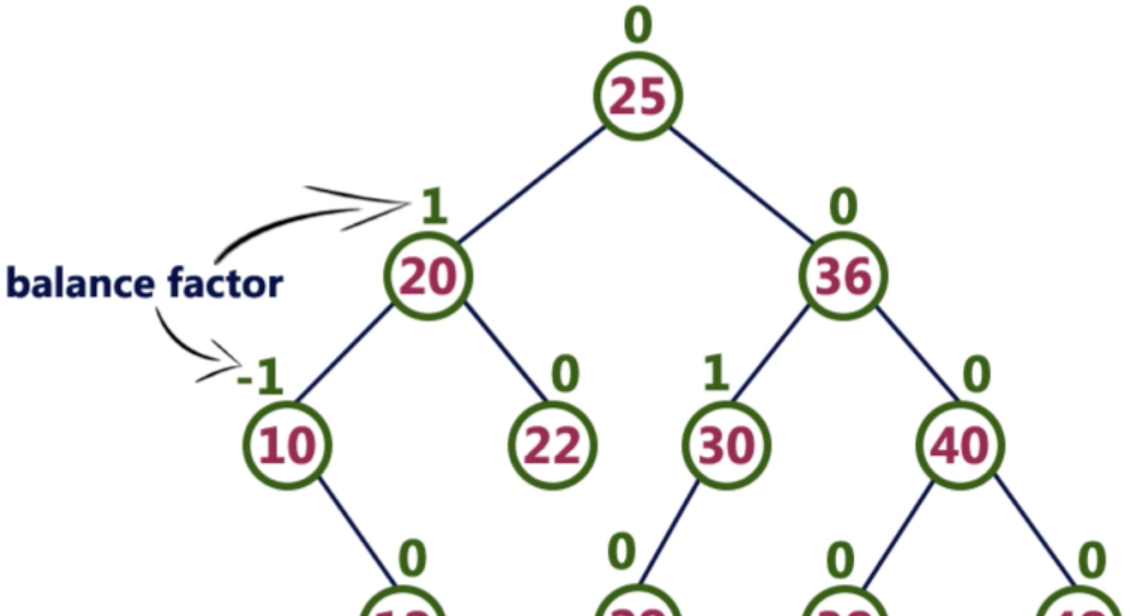
balance factor(平衡因子)記錄了左右子樹的高度差。上圖定義的是有左子樹沒有右子樹內插補點是1,沒有左子樹有右子樹內插補點是-1.
2、AVL樹具有以下性質
- 根的左右子樹的高度之差的絕對值不能超過1
- 根的左右子樹都是平衡二叉樹(任何一個節點的左右子樹高度差都不能超過1)
二、AVL樹插入和旋轉
插入一個節點可能會破壞AVL樹的平衡,可以通過旋轉操作來進行修正。
插入一個節點後,隻有從插入節點到根節點的路徑上的節點的平衡可能被改變。
我們需要找出第一個破壞了平衡條件的節點,稱之為K。K的兩顆子樹的高度差為2。
1、不平衡的出現有4種情況
(1)不平衡是由于對K的右孩子的右子樹插入導緻的
操作方法:左旋
(2)不平衡是由于對K的左孩子的左子樹插入導緻的
操作方法:右旋
(3)不平衡是由于對K的右孩子的左子樹插入導緻的
操作方法:右旋——左旋
(4)不平衡是由于對K的左孩子的右子樹插入導緻的
操作方法:左旋——右旋
2、旋轉代碼實作
from .bst import BiTreeNode, BST
class AVLNode(BiTreeNode):
def __init__(self, data):
BiTreeNode.__init__(self, data)
self.bf = 0 # 平衡因子,bf=-1:左邊樹比右邊高;bf=1:右邊樹比左邊高
class AVLTree(BST):
def __init__(self, li=None):
BST.__init__(self, li)
def insert_no_rec(self, val):
"""重寫插入方法"""
def rotate_left(self, p, c): # 根節點及其右孩子
"""對K的右孩子的右子樹插入導緻——左旋"""
s2 = c.lchild
p.rchild = s2
if s2: # 如果s2不為空
s2.parent = p
# C與P連結起來
c.lchild = p
p.parent = c
# 更新平衡因子
p.bf = 0
c.bf = 0
return c # 根節點
def rotate_right(self, p, c):
"""對K的左孩子的左子樹插入導緻——右旋"""
s2 = c.rchild
p.lchild = s2
if s2:
s2.parent = p
# C與P連結起來
c.rchild = p
p.parent = c
# 更新平衡因子
p.bf = 0
c.bf = 0
return c
def rotate_right_left(self, p, c):
"""由于對K的右孩子的左子樹插入導緻——右旋左旋"""
g = c.lchild # g節點是c的左孩子
# 右旋
s3 = g.rchild
c.lchild = s3 # c的左孩子綁定s3
if s3: # 如果s3存在
s3.parent = c # s3的父節點指向c(反鍊回去)
# G與C連結起來
g.rchild = c
c.parent = g
# 左旋
s2 = g.lchild
p.rchild = s2 # s2綁定給p的右孩子
if s2: # 如果s2存在
s2.parent = p
# G與P連結起來
g.lchild = p
p.parent = g
# 更新平衡因子
if g.bf > 0: # 插入的是s3,原G的右孩子
p.bf = -1 # p節點右邊是空的
c.bf = 0
elif g.bf < 0: # 插入的是s2,原G的左孩子
p.bf = 0
c.bf = 1 # c節點左邊是空的
else: # 插入的是G
p.bf = 0
c.bf = 0
def rotate_left_right(self, p, c):
"""由于對K的左孩子的右子樹插入導緻——左旋右旋"""
g = c.rchild # g節點是c的右孩子
# 左旋
s2 = g.lchild
c.rchild = s2 # c的右孩子綁定s2
if s2: # 如果s3存在
s2.parent = c # s2的父節點指向c(反鍊回去)
# G與C連結起來
g.lchild = c
c.parent = g
# 右旋
s3 = g.rchild
p.lchild = s3 # s3綁定給p的左孩子
if s3: # 如果s3存在
s3.parent = p
# G與P連結起來
g.rchild = p
p.parent = g
# 更新平衡因子
if g.bf < 0: # 插入的是s2,原G的左孩子
p.bf = 1
c.bf = 0
elif g.bf > 0: # 插入的是s3,原G的右孩子
p.bf = 0
c.bf = -1
else: # 插入的是G
p.bf = 0
c.bf = 0
3、根據AVL旋轉實作AVL插入
from bst import BiTreeNode, BST
class AVLNode(BiTreeNode):
def __init__(self, data):
BiTreeNode.__init__(self, data)
self.bf = 0 # 平衡因子,bf=-1:左邊樹比右邊高;bf=1:右邊樹比左邊高
class AVLTree(BST):
def __init__(self, li=None):
BST.__init__(self, li)
def rotate_left(self, p, c): # 根節點及其右孩子
"""代碼省略"""
def rotate_right(self, p, c):
"""代碼省略"""
def rotate_right_left(self, p, c):
"""代碼省略"""
def rotate_left_right(self, p, c):
"""代碼省略"""
def insert_no_rec(self, val):
"""重寫BST插入方法"""
# 1.第一步和BST一樣做插入
p = self.root
if not p: # 空樹的情況處理
self.root = AVLNode(val)
return
while True:
if val < p.data: # 添加值小于目前節點,往左邊走
if p.lchild: # 如果左孩子存在
p = p.lchild
else: # 左子樹不存在
p.lchild = AVLNode(val)
p.lchild.parent = p
node = p.lchild # node儲存插入的節點
break
elif val > p.data: # 大于根節點往右邊走
if p.rchild: # 如果右孩子存在
p = p.rchild
else: # 右子樹不存在
p.rchild = AVLNode(val)
p.rchild.parent = p
node = p.rchild # node儲存插入的節點
break
else: # 有一個一樣值的節點,什麼都不做
return
# 2.第二步更新平衡因子
while node.parent: # 如果node的父親不是空
if node.parent.lchild == node: # 傳遞是從左子樹來的,左子樹更沉了
# 更新node.parent的平衡因子 -= 1
if node.parent.bf < 0: # 原來node.parent.bf==-1,更新後變為-2
# 做旋轉
# 看node哪邊沉
g = node.parent.parent # 用于連接配接旋轉之後的子樹
x = node.parent # 旋轉前子樹的根
if node.bf > 0: # node右邊沉——》左右
n = self.rotate_left_right(node.parent, node)
else: # node左邊沉——》左左
n = self.rotate_right(node.parent, node)
# 注意要将n和g連起來
elif node.parent.bf > 0: # 原來node.parent.bf==1,更新後變為0
node.parent.bf = 0
break
else: # 原來node.parent.bf == 0,更新後變為-1
node.parent.bf = -1
node = node.parent # 往上走一層繼續循環
continue
else: # 傳遞是從右子樹來的,右子樹更沉了
# 更新node.parent.bf += 1
if node.parent.bf > 0: # 原來node.parent.bf==1,更新後變為2
# 做旋轉
# 看node哪邊沉
g = node.parent.parent # 用于連接配接旋轉之後的子樹
x = node.parent # 旋轉前子樹的根
if node.bf < 0: # node左邊沉——》右左
n = self.rotate_right_left(node.parent, node)
else: # node右邊沉——》右右
n = self.rotate_left(node.parent, node)
# 這裡不考慮等于0的情況,因為傳遞上來了,肯定是因為它的bf不為0
# 記得連起來
elif node.parent.bf < 0: # 原來node.parent.bf==-1,更新後變為0
node.parent.bf = 0
break # 因為是0,就不需要傳遞了
else: # 原來node.parent.bf == 0,更新後變為1
node.parent.bf = 1
node = node.parent # 往上走一層繼續循環
continue
# 連結旋轉後的子樹
n.parent = g
if g: # 如果g不是空
if x == g.lchild: # 如果旋轉之前子樹的根(x)是g的左孩子
g.lchild = n
else:
g.rchild = n
break
else: # 為空說明是根節點
self.root = n
break
tree = AVLTree([9,8,7,6,5,4,3,2,1])
tree.pre_order(tree.root)
print("")
tree.in_order(tree.root)
"""
6,4,2,1,3,5,8,7,9,
1,2,3,4,5,6,7,8,9,
"""