較長的描述,好像跟我自己寫的差不多......不過終究是大神級别,講的就是透徹
1. 概述
AVL樹是最早提出的自平衡二叉樹,在AVL樹中任何節點的兩個子樹的高度最大差别為一,是以它也被稱為高度平衡樹。AVL樹得名于它的發明者G.M. Adelson-Velsky和E.M. Landis。AVL樹種查找、插入和删除在平均和最壞情況下都是O(log n),增加和删除可能需要通過一次或多次樹旋轉來重新平衡這個樹。
2. 基本術語
有四種種情況可能導緻二叉查找樹不平衡,分别為:
(1)LL:插入一個新節點到根節點的左子樹(Left)的左子樹(Left),導緻根節點的平衡因子由1變為2
(2)RR:插入一個新節點到根節點的右子樹(Right)的右子樹(Right),導緻根節點的平衡因子由-1變為-2
(3)LR:插入一個新節點到根節點的左子樹(Left)的右子樹(Right),導緻根節點的平衡因子由1變為2
(4)RL:插入一個新節點到根節點的右子樹(Right)的左子樹(Left),導緻根節點的平衡因子由-1變為-2
針對四種種情況可能導緻的不平衡,可以通過旋轉使之變平衡。有兩種基本的旋轉:
(1)左旋轉:将根節點旋轉到(根節點的)右孩子的左孩子位置
(2)右旋轉:将根節點旋轉到(根節點的)左孩子的右孩子位置
3. AVL樹的旋轉操作
AVL樹的基本操作是旋轉,有四種旋轉方式,分别為:左旋轉,右旋轉,左右旋轉(先左後右),右左旋轉(先右後左),實際上,這四種旋轉操作兩兩對稱,因而也可以說成兩類旋轉操作。
基本的資料結構:
1 typedef struct Node* Tree;
2 typedef struct Node* Node_t;
3 typedef Type int;
4
5 struct Node{
6 Node_t left;
7 Node_t right;
8 int height;
9 Type data;
10 };
11 int Height(Node_t node) {
12 return node->height;
13 } 3.1 LL
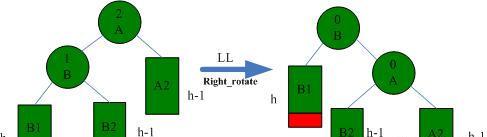
LL情況需要右旋解決,如下圖所示:
1 Node_t RightRotate(Node_t a) {
2 b = a->left;
3 a->left = b->right;
4 b->right = a;
5 a->height = Max(Height(a->left), Height(a->right));
6 b->height = Max(Height(b->left), Height(b->right));
7 return b;
8 } 3.2 RR
RR情況需要左旋解決,如下圖所示:
1 Node_t LeftRotate(Node_t a) {
2 b = a->right;
3 a->right = b->left;
4 b->left = a;
5 a->height = Max(Height(a->left), Height(a->right));
6 b->height = Max(Height(b->left), Height(b->right));
7 return b;
8 } 3.3 LR
LR情況需要左右(先B左旋轉,後A右旋轉)旋解決,如下圖所示:
1 Node_t LeftRightRotate(Node_t a) {
2 a->left = LeftRotate(a->left);
3 return RightRotate(a);
4 } 3.4 RL
RL情況需要右左旋解決(先B右旋轉,後A左旋轉),如下圖所示:
1 Node_t RightLeftRotate(Node_t a) {
2 a->right = RightRotate(a->right);
3 return LeftRotate(a);
4 } 4. AVL數的插入和删除操作
(1) 插入操作:實際上就是在不同情況下采用不同的旋轉方式調整整棵樹,具體代碼如下:
1 Node_t Insert(Type x, Tree t) {
2 if(t == NULL) {
3 t = NewNode(x);
4 } else if(x < t->data) {
5 t->left = Insert(t->left);
6 if(Height(t->left) - Height(t->right) == 2) {
7 if(x < t->left->data) {
8 t = RightRotate(t);
9 } else {
10 t = LeftRightRotate(t);
11 }
12 }
13 } else {
14 t->right = Insert(t->right);
15 if(Height(t->right) - Height(t->left) == 2) {
16 if(x > t->right->data) {
17 t = LeftRotate(t);
18 } else {
19 t = RightLeftRotate(t);
20 }
21 }
22 }
23 t->height = Max(Height(t->left), Height(t->right)) + 1;
24 return t;
25 } (2) 删除操作:首先定位要删除的節點,然後用該節點的右孩子的最左孩子替換該節點,并重新調整以該節點為根的子樹為AVL樹,具體調整方法跟插入資料類似,代碼如下:
1 Node_t Delete(Type x, Tree t) {
2 if(t == NULL) return NULL;
3 if(t->data == x) {
4 if(t->right == NULL) {
5 Node_t temp = t;
6 t = t->left;
7 free(temp);
8 } else {
9 Node_t head = t->right;
10 while(head->left) {
11 head = head->left;
12 }
13 t->data = head->data; //just copy data
14 t->right = Delete(t->data, t->right);
15 t->height = Max(Height(t->left), Height(t->right)) + 1;
16 }
17 return t;
18 } else if(t->data < x) {
19 Delete(x, t->right);
20 if(t->right) Rotate(x, t->right);
21 } else {
22 Delete(x, t->left);
23 if(t->left) Rotate(x, t->left);
24 }
25 if(t) Rotate(x, t);
26 } 5. 總結
AVL樹是最早的自平衡二叉樹,相比于後來出現的平衡二叉樹(紅黑樹,treap,splay樹)而言,它現在應用較少,但研究AVL樹對于了解後面出現的常用平衡二叉樹具有重要意義。
作者:xingoo