本節書摘來自華章出版社《資料庫原理與應用(第3版)》一 書中的第3章,第3.5節,作者:何玉潔,更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視。
關系模型源于數學。關系是由元組構成的集合,可以通過關系的運算來表達查詢要求,而關系代數恰恰是關系操作語言的一種傳統的表示方式,它是一種抽象的查詢語言。
關系代數的運算對象是關系,運算結果也是關系。與一般的運算一樣,運算對象、運算符和運算結果是關系代數的三大要素。
關系代數的運算可分為兩大類:
傳統的集合運算。這類運算完全把關系看成元組的集合。傳統的集合運算包括集合的廣義笛卡兒積運算、并運算、交運算和差運算。
專門的關系運算。這類運算除了把關系看成元組的集合外,還通過運算表達了查詢的要求。專門的關系運算包括選擇、投影、連接配接和除運算。
關系代數中的運算符可以分為四類:傳統的集合運算符、專門的關系運算符、比較運算符和邏輯運算符。表3-9列出了這些運算符,其中比較運算符和邏輯運算符是配合專門的關系運算符來構造表達式的。
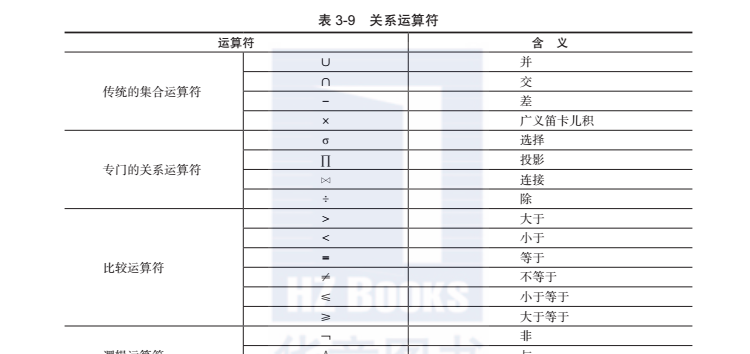
傳統的集合運算是二目運算,設關系r和s均是n元關系,且相應的屬性值取自同一個值域,則可以定義三種運算:并運算(∪)、交運算(∩)和差運算(-),但廣義笛卡兒積并不要求參與運算的兩個關系的對應屬性取自相同的域。并、交、差運算的功能示意圖如圖3-5所示。
現在我們以圖3-6a和圖3-6b所示的兩個關系為例,說明這三種傳統的集合運算功能。
1.?并運算
關系r與關系s的并記為:
r∪s = {t | t∈r ∨ t∈s}
其結果仍是n目關系,由屬于r或屬于s的元組組成。
圖3-7a顯示了圖3-6a和圖3-6b兩個關系的并運算結果。
2.?交運算
關系r與關系s的交記為:
r∩s = {t | t∈r ∧ t∈s }
其結果仍是n目關系,由屬于r并且也屬于s的元組組成。
圖3-7b顯示了圖3-6a和圖3-6b兩個關系的交運算結果。
3.?差運算
關系r與關系s的差記為:
r - s = {t | t∈r ∧ t∈s }
圖3-7c顯示了圖3-6a和圖3-6b兩個關系的交運算結果。
4.?廣義笛卡兒積
廣義笛卡兒積不要求參加運算的兩個關系具有相同的目。
兩個分别為m目和n目的關系r和關系s的廣義笛卡兒積是一個(m+n)目的元組的集合。元組的前m個列是關系r的一個元組,後n個列是關系s的一個元組。若r有k1個元組,s有k2個元組,則關系r和關系s的廣義笛卡兒積有k1×k2個元組,記作:
r×s = { tr ^ ts | tr∈r ∧ ts∈s }
tr ^ ts表示由兩個元組tr和ts前後有序連接配接而成的一個元組。
任取元組tr和ts,當且僅當tr屬于r且ts屬于s時,tr和ts的有序連接配接即為r×s的一個元組。
實際操作時,可從r的第一個元組開始,依次與s的每一個元組組合,然後,對r的下一個元組進行同樣的操作,直至r的最後一個元組也進行同樣的操作為止,即可得到r×s的全部元組。
圖3-8所示為廣義笛卡兒積的操作示意。
專門的關系運算包括投影、選擇、連接配接和除等操作,其中選擇和投影為一進制操作,連接配接和除為二進制操作。
下面我們以表3-10~表3-12所示的三個關系為例,介紹專門的關系運算。各關系包含的屬性含義如下。
student:sno(學号),sname(姓名),ssex(性别),sage(年齡),sdept(所在系)。
course:cno(課程号),cname(課程名),credit(學分),semester(開課學期)。
sc:sno(學号),cno(課程号),grade(成績)。
1.?選擇
選擇(selection)運算是最簡單的運算,它從指定的關系中選擇某些元組形成一個新的關系,被選擇的元組是滿足指定的邏輯條件的。
選擇運算表示為:
σf (r) ={ t | t∈r ∧ f(t)= ‘真’ }
其中,σ是選擇運算符,r是關系名,t是元組,f是邏輯表達式,取邏輯“真”值或“假”值。
例3-4 查詢計算機系的學生資訊。
σsdept = ‘計算機系’(student)
結果如圖3-9所示。
2.?投影
投影(projection)運算是對指定的關系進行垂直方向的選擇,并形成一個新的關系。該操作包括如下兩個過程:
1)選擇指定的屬性,形成一個可能含有重複行的關系。
2)删除重複行,形成新的關系。
投影運算表示為:
∏ a (r) = { t.a | t∈r }
其中,∏是投影運算符,r是關系名,a是被投影的屬性或屬性組。t.a表示t這個元組中對應屬性(集)a的分量,也可以表示為t [a]。
例3-5 查詢學生的姓名和所在系。
∏sname, sdept(student)
結果如圖3-10所示。
3.?連接配接
連接配接運算用來連接配接互相之間有聯系的兩個關系,進而産生一個新的關系。這個過程由連接配接屬性(字段)來實作。一般情況下這個連接配接屬性是出現在不同關系中的語義相同的屬性。
連接配接運算也稱為θ運算。連接配接運算一般表示為:
其中a和b分别是關系r和s上語義相同的屬性或屬性組,θ是比較運算符。連接配接運算從r和s的廣義笛卡兒積r×s中選擇(r關系)在a屬性組上的值與(s關系)在b屬性組上值滿足比較運算符θ的元組。
連接配接運算中最重要也是最常用的連接配接有兩個,一個是等值連接配接,一個是自然連接配接。
當θ為“=”時的連接配接為等值連接配接,它是從關系r與關系s的廣義笛卡兒積中選取a、b屬性值相等的那些元組,即:
自然連接配接是一種特殊的連接配接,它要求兩個關系中進行比較的分量必須是相同的屬性組,并且在結果中要去掉重複的屬性列。即,若關系r和s具有相同的屬性組b,則自然連接配接可記作:
一般的連接配接運算是從行的角度進行運算,但自然連接配接還需要去掉重複的列,是以是同時從行和列的角度進行運算。
自然連接配接與等值連接配接的差别為:
自然連接配接要求相等的分量必須有共同的屬性名,等值連接配接則不要求。
自然連接配接要求把重複的屬性名去掉,等值連接配接卻不這樣做。
例3-6 對表3-10和表3-12所示的student和sc關系,分别進行如下的等值連接配接和自然連接配接運算。
等值連接配接:
自然連接配接:
等值連接配接的結果如圖3-11所示,自然連接配接的結果如圖3-12所示。
4.?除
1)除(division)運算的簡單描述。
設關系s的屬性是關系r的屬性的一部分,則r÷s為這樣一個關系:
此關系的屬性是由屬于r但不屬于s的所有屬性組成。
r÷s的任一進制組都是r中某元組的一部分。但必須符合下列要求,即任取屬于r÷s的一個元組t,則t與s的任一進制組連接配接後,都為r中原有的一個元組。
除運算的示意圖如圖3-13所示。
2)除運算的一般形式。設有關系r(x,y)和s(y,z),其中x、y、z為關系的屬性組,則:
r(x,y) ÷s(y,z) = r(x,y) ÷ ∏y (s)
3)關系的除運算是關系運算中最複雜的一種,關系r與s的除運算的以上叙述解決了r÷s關系的屬性組成及其元組應滿足的條件要求,但怎樣确定r÷s的元組仍然沒有說清楚。為了說清楚這個問題,首先引入象集的概念。
象集(image set):給定一個關系r(x,y),x和y為屬性組。定義,當t[x] = x時,x在r中的象集為:
yx ={t[y] | t∈r∧t[x] = x}
上式中:t [y]和t [x]分别表示r中的元組t在屬性組y和x上的分量的集合。
例如在表3-10所示的student關系中,有一個元組值為:
(0521101,張立,男,22,資訊系)
假設x = {sdept,ssex},y = {sno,sname,sage},則上式中的t[x]的一個值
x = (資訊系,男)
此時,yx為t[x] = x = (資訊系,男)時所有t[y]的值,即:
yx = { (0521101,張立,22),(0521103,張海,20) }
也就是由資訊系全體男生的學号、姓名、年齡所構成的集合。
又例如,對于表3-12所示的sc關系,如果設x = {sno},y = {cno,grade},則當x取“0512101”時,y的象集為:
yx = { (c01,90),(c02,86) }
當x取“0521102”時,y的象集為:
yx = {(c01,82),(c02,75),(c04,92),(c05,50)}
現在,我們再回過頭來讨論除法的一般形式。
設有關系r (x,y)和s (y,z),其中x、y、z為關系的屬性組,則:
r÷s = {tr [x] | tr∈r ∧ ∏y (s) yx}
圖3-14給出了一個除運算的示例。
圖3-14所示的除結果為至少選了“c01”和“c02”兩門課程的學生的學号。
下面以表3-10~表3-12所示的student、course和sc關系為例,給出一些關系代數運算的綜合例子。
例3-7 查詢選了c02号課程的學生的學号和成績。
∏sno, grade (σcno=‘c02’ (sc))
運算結果如圖3-15所示。
例3-8 查詢資訊系選了c04号課程的學生的姓名和成績。
由于學生姓名資訊在student關系中,而成績資訊在sc關系中,是以這個查詢同時涉及student和sc兩個關系。是以首先應對這兩個關系進行自然連接配接,得到同一位學生的有關資訊,然後再對連接配接的結果執行選擇和投影操作。具體如下:
∏sname, grade(σcno=‘c04’∧sdept=‘資訊系’(sc student))
也可以寫成:
∏sname, grade(σcno=‘c04‘(sc) σsdept=‘資訊系‘(student))
後一種實作形式是首先在sc關系中查詢出選了“c04”課程的集合,然後從student關系中查詢出“資訊系”學生的集合,最後再對這個集合進行自然連接配接運算(sno相等),這種查詢的執行效率會比第一種形式高。
運算結果如圖3-16所示。
例3-9 查詢選了第2學期開設的課程的學生的姓名、所在系和所選的課程号。
這個查詢的查詢條件和查詢列與兩個關系有關:student(包含姓名和所在系資訊)以及course(包含課程号和開課學期資訊)。但由于student關系和course關系之間沒有可以進行連接配接的屬性(要求必須語義相同),是以,如果要讓student關系和course關系進行連接配接,則必須要借助于sc關系,通過sc關系中的sno與student關系中的sno進行自然連接配接,并通過sc關系中的cno與course關系中的cno進行自然連接配接,可實作student關系和course關系之間的關聯關系。
該示例的關系代數表達式如下:
∏sname, sdept, cno(σsemester=2(course sc student))
∏sname, sdept, cno(σsemester=2(course) sc student)
運算結果如圖3-17所示。
例3-10 查詢選了“vb”課程且考試成績大于等于80的學生姓名、所在系和成績。
這個查詢涉及student、sc和course三個關系,在course關系中可以指定課程名,從student關系中可以得到姓名、所在系,從sc關系中可以得到成績。
∏sname, sdept, grade(σcname=‘vb’ ∧ grade>=80(course sc student))
∏sname, sdept, grade(σcname=‘vb’(course) σgrade>=80(sc) student)
運算結果如圖3-18所示。
例3-11 在全體學生中查詢未選“計算機文化學”的學生姓名和所在系。
實作這個查詢的關系代數表達式的基本思路是:從全體學生中去掉選了“計算機文化學”課程的學生,是以需要用到差運算。這個查詢同樣涉及student、sc和course三個關系。
∏sname, sdept(student)- ∏sname, sdept(σcname=‘計算機文化學’(course sc student))
∏sname, sdept(student)- ∏sname, sdept(σcname=‘計算機文化學’(course) sc student)
運算結果如圖3-19所示。
圖3-12 查詢選了全部課程的學生的姓名和所在系。
編寫實作這個查詢的關系代數表達式的思考過程如下:
1)學生選課情況可用∏sno,cno(sc)表示。
2)全部課程可用∏cno(course)表示。
3)查詢選了全部課程的學生的學号,可用除法運算得到,即:
∏sno,ono (sc) ÷∏cno (course)
4)從得到的sno集合再在student關系中找到對應的學生姓名(sname)和所在系(sdept),可用自然連接配接和投影操作組合實作。最終的關系代數表達式如下:
∏sname, sdept(student (∏sno,cno (sc) ÷∏cno (course)))
運算結果為空集合。
例3-13 查詢資訊系選了第2學期開設的全部課程的學生的學号和姓名。
編寫實作這個查詢的關系代數表達式的思考過程與例3-12類似,隻是将2)改為“查詢第2學期開設的全部課程”,這可用下清單達式表達:
∏cno (σsemester=2(course)
最終的關系代數表達式為:
∏sno, sname(σsdept=‘資訊系’(student) (∏ sno,cno (sc) ÷ ∏cno(σsemester=2(course))))
運算結果如圖3-20所示。
表3-13對關系代數操作進行了總結。
關系運算的優先級按從高到低的順序為:投影、選擇、笛卡兒乘積、連接配接和除(同級)、交、并和差(同級)。