本節書摘來自華章出版社《r語言資料挖掘:實用項目解析》一書中的第2章,第2.5節解讀分布,作者[印度]普拉迪帕塔·米什拉(pradeepta mishra),更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視
2.5 解讀分布
計算機率分布、将資料點拟合于一些特定類型的分布以及後續的解讀有助于建立假設。此假設可用于在給定一組參數下估算事件的機率。我們來看看對不同類型分布的解讀。
解讀連續型資料
一個資料集的任何變量都可通過拟合一個分布來得到其分布參數的最大似然估計。密度函數适用于諸如“貝塔”“柯西”“卡方”“指數”“f”“伽馬”“幾何”“對數正态”“logistic”“負二項”“正态”“泊松”“t”和“威布爾”等分布。這些分布都是常用的,這裡不給出示例。對于連續型資料,我們采用正态分布和t分布:
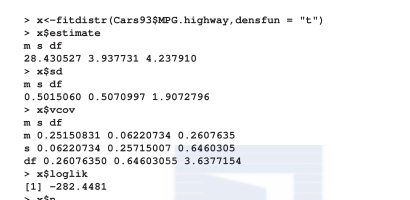
在上面的代碼中,我們用的是cars93資料集中的mpg.highway變量。通過讓t分布拟合這個變量,我們得到參數估計、标準誤差估計、協方差矩陣估計、對數似然值還有總數。類似的操作也适用于對連續型變量執行正态分布拟合:
現在我們來看如何圖形化地表示變量的正态性:
可以看到,所表示的偏離的資料點距離直線很遠。
下面解讀離散資料,因為其中有所有分類:
為了将結果可視化,我們需要用到下圖所示的盒狀圖: