本節書摘來自華章出版社《r語言資料挖掘:實用項目解析》一書中的第2章,第2.4節解讀分布和變換,作者[印度]普拉迪帕塔·米什拉(pradeepta mishra),更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視
2.4 解讀分布和變換
為了對所有統計假設檢驗的前提假設有清晰的認識,了解機率分布至關重要。例如,線上性回歸分析中,基本的前提假設是誤差分布呈正态分布且變量關系為線性。是以在建立模型之前,觀察分布的形狀并采取可能的校正變換是很重要的,如此才能便于對這些變量使用更深入的統計技術。
2.4.1 正态分布
正态分布原理基于中心極限定理(clt),表示從一個均值為μ、方差為σ2的總量中抽取的所有大小為n的樣本,在n增長趨于無窮時,其分布都近似于一個均值為μ、方差為σ2的正态分布。檢查變量的正态性對于移除離群點很重要,因為這樣才會使得預測過程不會受影響。離群點的存在不僅會使預測值偏離,也會影響預測模型的穩定性。接下來的示例代碼和圖将示範如何圖像化地檢測并解釋正态性。
為了檢測出正态分布,我們可以使用其中一些變量的平均值、中位數和衆數:
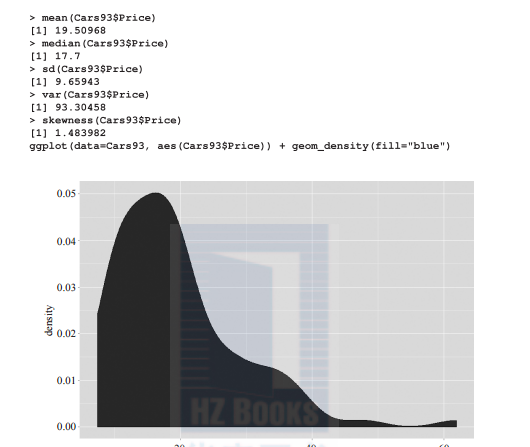
從上圖可以得出這樣的結論,price變量是正偏斜的,因為一些離群點在分布的右邊。price的平均值被誇大且大于衆數,因為平均值受到極端值波動的影響。
現在我們嘗試了解一個可用正态分布解答假設的案例。
假設變量mpg.highway(高速路上每加侖油耗可行駛的英裡數)呈均值為29.08和标準差為5.33的正态分布,一輛新車每加侖油耗可行駛35英裡(約56km)的機率是多少?
是以要求一輛新車每加侖油耗可以行駛35英裡的機率是13.36%。因為期望均值高于實際均值,是以lower.tail設為f。
2.4.2 二項分布
二項分布也被稱為離散機率分布,它描述的是一個試驗的結果。每一次試驗均假定隻有兩種結果:要麼為成功或失敗,要麼為是或否。舉個例子,cars93資料集中,是否手動變速(manual transmission availability)就被表示成yes或no。
下面以一個例子來解釋二項分布可以用在什麼地方。對于一輛有缺陷的汽車,有一個特定零件功能壞了的機率是0.1%。假設有93輛已制造好的汽車,至少一輛有缺陷的汽車可被檢測出來的機率是多大:
是以要求的93輛汽車中的有缺陷汽車機率是0.0006,與一個損壞零件的機率0.10相比,這是個非常小的數字。
2.4.3 泊松分布
泊松分布針對的是計數資料,給定關于一個事件的資料與資訊,利用泊松機率分布,你可以預測在極限範圍内任一數字出現的機率。
我們來看一個例子。假設平均每分鐘有200位顧客通路某電商網站,可得一分鐘内會有250個顧客通路同一個網站的機率:
是以,所求的機率是0.0002,說明這種情況很罕見。除了上述常見的機率分布,還有一些分布可用于罕見情況。