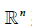本節書摘來自華章出版社《 線性代數及其應用 (原書第4版)》一書中的第1章,第1.9節,作者:(美)戴維c. 雷(david c. lay)馬裡蘭大學帕克學院 著劉深泉 張萬芹 陳玉珍 包樂娥 陸 博 譯,更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視
當一個線性變換 t是由幾何中提出來或用語言叙述時,我們通常希望有關于 t(x)的公式. 下面的讨論指出,從
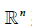 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 到
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的每一個線性變換,實際上都是一個矩陣變換
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,而且變換 t的性質都歸結為 a的性質. 尋找矩陣 a的關鍵,是了解 t完全由它對機關矩陣
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的各列的作用所決定.
例1
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的兩列是
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 和
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,設t 是
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 licdn.com/31ce0ad44fd4f272717e909d0027c8f5e18dfb7a.png)的線性變換,使
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 求出
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中任意向量x 的像.
解 寫出
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 因為t 是線性變換,是以
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 (2)
由步驟(1)到(2)說明為什麼隻要知道
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 就可由任意 x決定
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,此外,因(2)把
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 表示為
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的線性組合,我們可把這些向量作為矩陣 a的各列,而把(2)式寫成
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 定理10 設
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 為線性變換,則存在唯一的矩陣 a,使
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 事實上, a是 m*n矩陣,它的第 j列是向量
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,其中
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 是機關矩陣
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的第 j列:
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 (3)
證 記
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,由于 t是線性變換,知
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 a 的唯一性在習題33中研究.
(3)中矩陣 稱為線性變換t的标準矩陣.
現在我們知道,由
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的每個線性變換都是矩陣變換,反之亦然. 術語線性變換強調映射的性質,而矩陣變換描述這樣的映射如何實作. 如下例所示.
例2 對拉伸變換t(x)=3x ,求标準矩陣.
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 例3 設
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 為把
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中每一個點逆時針旋轉角度
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的變換. 我們可以證明這個變換是線性變換(見1.8節圖1-39),求出這個變換的标準矩陣.
解
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 旋轉成為
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,見圖1-41.
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 由定理10,
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 1.8節例5是這個變換的特殊情形,其中
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 .
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中的幾何線性變換
例2和例3說明了幾何中的線性變換,表1-2~1-5說明了其他常見的平面幾何線性變換. 因這些變換都是線性的,它們完全由它們對
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的各列的作用确定,而不是僅表示
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的像,下列各表說明了這些變換對機關正方形的作用(見圖1-42).
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 其他的變換可以通過表1-2~1-5所列出的變換通過複合構造出來,即一個變換之後再作另一個變換,例如,作一個水準剪切變換後再做一個關于
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 軸的對稱變換. 2.1節将證明,線性變換的複合仍是線性的(見習題34).
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 存在與唯一性問題
線性變換的概念給出一種新的了解以前提到的存在唯一性問題的觀點,下列兩個定義給出與變換有關的術語.
定義 映射
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 稱為到
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 上的映射,若
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中任一 b都至少有一個
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中的 x與之對應.(也稱為滿射.)
等價地,當 t的值域是整個餘定義域
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 時, t是到
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 上的. 也就是說,若對
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中每個 b,方程t(x)=b 至少有一個解.“t 是否把
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 映到
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 上?”是存在性問題. 映射t不是到
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 上的,若
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中有某個b使方程t(x)=b無解. 見圖1-43.
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 稱為一對一映射(或1:1),若
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中每個b 是
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中至多一個x 的像. (也稱為單射.)
等價地, t是一對一的,若對
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中每個b ,方程 t(x)=b有唯一的解或沒有解.“ t是否是一對一的?”是唯一性問題. 映射 t不是一對一的,若
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中某個b是
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中多個向量的像. 若沒有這樣的 b, t就是一對一的. 見圖1-44.
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 表1-5中的投影變換不是一對一的,也不能将
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 映上到
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 . 表1-2、1-3和1-4中的變換是一對一的,能将
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 . 其他可能性在下面的兩個例子中給出.
例4及随後的定理說明了關于一對一映射與映上映射的函數性質是如何與本章以前的一些概念關聯起來的.
例4 設t是線性變換,它的标準矩陣為
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 t是否把
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ?t 是否一對一映射?
解 因 a已經是階梯形,可以立即看出, a在每一行有主元位置,由1.4節定理4,對
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中每個b ,方程ax=b 相容,換句話說,線性變換t 将
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 (它的定義域)映射到
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 上. 然而因方程 ax=b有一個自由變量(因為有4個變量,僅有3個基本變量),每個 b 都有多個 x 的像,是以 t不是一對一的.
定理11 設
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 為線性變換,則t 是一對一當且僅當方程ax=0 僅有平凡解.
證 因 t是線性的,t(0)=0 ,若 t是一對一的,方程t( x)=0至多有一個解,是以僅有零解. 若 t不是一對一的,則
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中某個 b是至少
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中兩個相異向量,比如說是u和v的像,即 t(u)=b,t(v)=b,于是因 t是線性的.
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 向量 u-v不是零,因
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 . 是以方程t(x)=0 有多于一個解. 因而定理中兩個條件同時成立或同時不成立.
定理12 設
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 是線性變換,設a 為 t的标準矩陣,則
t 把
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 映上到 ,當且僅當 的a列生成
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 t 是一對一的,當且僅當 a 的列線性無關.
證 a. 由1.4節定理4,a 的列生成
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 當且僅當方程 ax=b對每個b 都相容,換句話說,當且僅當對每個 b,方程t(x)=b 至少有一個解,這就是說, t将
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 映射到
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 上.
方程t(x)=0和ax=0 僅有記法不同. 是以由定理11, t 是一對一的當且僅當 ax=0僅有平凡解,在1.7節(3)的命題已說明,這等價于a 的各列線性無關.
定理12的命題(a)等價于命題“ t把
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,當且僅當
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 中的任一向量都是 a的列的一個線性組合.”參見1.4節定理4.
下例以及習題中,我們把列向量寫成行的形式,如
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,将 t(x)寫成
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,以代替更正式的
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 例5 設
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,證明t 是一對一線性變換. t 是否将
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ?
解 當 x和 t(x)寫成列向量,容易通過檢查ax 中每個元素的行-向量計算看出 t的标準矩陣.
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 (4)
故t 的确是線性變換,它的标準矩陣如(4)所示. a的列是線性無關的,因為它們互相之間不是倍數關系,由定理12(b), t是一對一的. 為确定t 是否從
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的映上映射,觀察 a的各列生成的向量集. 因 a是3*2矩陣,由定理4可知, a的列生成
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 當且僅當 a有3個主元列. 這是不可能的,因 a僅有2列,是以a 的各列不能生成
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 ,對應的線性變換不是映上到
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的. 如圖1-45所示.
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 練習題
設
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 為一個線性變換,它先作水準剪切變換,将
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 映射為
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 (但
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 不變),然後再做關于
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 軸的對稱變換. 假設 t是線性的,求它的标準矩陣.(提示:确定
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣 的像的最終位置.)
習題1.9
 《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣  《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣
《 線性代數及其應用 (原書第4版)》——1.9 線性變換的矩陣