本節書摘來自華章出版社《 線性代數及其應用 (原書第4版)》一書中的第1章,第1.6節,作者:(美)戴維c. 雷(david c. lay)馬裡蘭大學帕克學院 著劉深泉 張萬芹 陳玉珍 包樂娥 陸 博 譯,更多章節内容可以通路雲栖社群“華章計算機”公衆号檢視
你也許希望現實生活中涉及線性代數的問題會是隻有唯一解,或者可能無解. 本節的意圖是要說明有多解的線性方程組是如何自然産生的. 這裡的執行個體來自經濟學、化學和網絡流.
經濟學中的齊次線性方程組
本章介紹中提到的500個變量的500個方程組成的方程組,現稱為列昂惕夫“投入-産出”(或“生産”)模型.1 2.6節将詳細讨論這個模型,那時我們有更多的理論和更好的符号. 目前,我們先看一個簡單的“交易模型”,這個模型也是由列昂惕夫提出的.
假設一個國家的經濟可以劃分為許多部門,如各種制造、交通、娛樂和服務業. 假設我們知道每個部門年度的總産出,并精确知道該總産出是如何在其他經濟部門進行配置設定或“交易”的. 稱一個部門産出的總貨币價值為該産出的價格. 列昂惕夫證明了下面的結論.
存在能夠指派給各個部門總産出的平衡價格,使得每個部門的總收入恰等于它的總支出.
下面的例子說明如何求平衡價格.
例1 假設一個經濟由煤炭、電力(電源)和鋼鐵三個部門組成,各部門之間的配置設定如表1-1所示,其中每一列中的數表示該部門總産出的比例. 如表1-1的第二列,将電力的總産出配置設定如下:40%給煤炭部門,50%給鋼鐵部門,剩下10%給電力部門.(電力部門把這10%作為運轉費用.)因所有産出都必須配置設定,每一列的分數之和等于1.
記符号
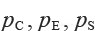
分别表示煤炭、電力和鋼鐵部門年度總産出的價格(即貨币價值). 如果可能,求平衡價格使每個部門的收支平衡.
解 某一部門所在的一清單示它的産出的去向,它所在的一行表示它從哪些部門獲得了投入. 例如,表1-1的第一行說明煤炭部門接受(采購)40%的電力産出和60%的鋼鐵産出. 因為相應部門的總産出價格為
和
,煤炭部門必須支付電力部門
美元,支付鋼鐵部門
美元,是以煤炭部門的總支出是
美元. 為使煤炭部門的總收入pc 等于它的總支出,有
(1)
交易表的第二行說明電力部門的開支有 0.6pc美元采購煤炭,
美元采購電力,
美元采購鋼鐵.是以電力部門的收支平衡條件是
(2)
最後,交易表的第三行導出最後的條件:
(3)
為求解方程組(1)、(2)、(3),将所有未知量移到方程的左邊并合并同類項. (例如,在方程(2)的左邊将
寫成
.)
接下來進行行簡化. 為簡明起見,數值舍入到小數點後兩位.
通解是
,
為自由變量. 這個經濟問題的平衡價格向量為
任意(非負)
取值可以算出平衡價格的一種取值. 例如,如果取
為100(或1億美元),那麼
.即如果煤炭的産出價格是9 400萬美元,電力的産出價格是8 500萬美元,鋼鐵的産出價格是1億美元,那麼每個部門的總收入和總支出将會相等.
配平化學方程式
化學方程式描述了化學反應的物質消耗和生産的數量. 例如,當丙烷氣體燃燒時,丙烷(c3h8)與氧(o2)結合生成二氧化碳(co2)和水(h2o),按照如下形式的一個方程式
為“配平”這個方程式,化學家必須找到
的全體數量,使得方程式左邊碳(c)、氫(h)、氧(o)原子的總數等于右邊相應原子的總數(因為在化學反應中原子既不會被破壞,也不會被創造).
配平化學方程式的一個系統方法是建立描述一個化學反應中每一種類型的原子的數目的一個向量方程. 由于方程式(4)包含三種類型的原子(碳、氫、氧),給(4)式的每一種反應物和生成物構造一個屬于
的向量,列出每個分子的組成原子的數目如下:
要配平方程式(4),
的系數必須滿足
将全部項移到等式左邊(修改第三和第四個向量的符号),得到:
行化簡該方程組的增廣矩陣得到通解
因為化學方程式的系數應為整數,取
,那麼
. 配平的方程式為
如果方程式中的每個系數乘兩倍(比如說),該方程式仍然是配平的. 然而在一般情形下,化學家傾向于使用全體系數盡可能小的數來配平方程式.
網絡流
當科學家、工程師或經濟學家研究一些數量在網絡中的流動時自然推導出線性方程組. 例如,城市規劃和交通工程人員監控一個網格狀的市區道路的交通流量模式;電氣工程師計算流經電路的電流;以及經濟學家分析通過分銷商和零售商的網絡從制造商到顧客的産品銷售. 許多網絡中的方程組涉及成百甚至上千的變量和方程.
一個網絡包含一組稱為接合點或節點的點集,并由稱為分支的線或弧連接配接部分或全部的節點. 流的方向在每個分支上有标示,流量(速度)也有顯示或用變量标記.
網絡流的基本假設是網絡的總流入量等于總流出量,且流經一個節點的總輸入等于總輸出. 例如,圖1-28顯示30單元經過一個分支流入一個節點,
标記該節點經過其他分支的流出. 因為流量在每個節點中是守恒的,我們有
. 類似地,每個節點的流量可以用一個方程描述. 網絡分析的問題就是确定當局部資訊(如網絡的輸入)已知時每一分支的流量.
例2 圖1-29中的網絡是巴爾的摩市區一些單行道路在一個下午早些時候(以每小時車輛數目計算)的交通流量. 計算該網絡的車流量.
解 寫出該流量的方程組,并求其通解. 如圖1-29所示,标記道路交叉口(節點)和未知的分支流量. 在每個交叉口,令其車輛駛入數目等于車輛駛出數目.
并且,網絡中的總流入量(500+300+100+400)等于總流出量(300+
+600),經簡化得
=400 . 該方程與上面四個方程聯立并重排後得到下面的方程組:
行化簡相應的增廣矩陣得到
該網絡的車流量為
網絡分支中的一個負流量對應模型中顯示方向相反的流量. 由于本問題中的道路是單行線,這裡不允許有負值變量. 這種情況給變量的可能取值增加了某種限制. 例如,因為
不能取負值,是以
. 其他變量的限制在練習題2中有考慮.
練習題
假設一個經濟有農業、礦業和制造業三個部門. 農業部門銷售它的産出的5%給礦業部門,30%給制造業部門,保留餘下的産出. 礦業部門銷售它的産出的20%給農業部門,70%給制造業部門,保留餘下的産出. 制造業部門銷售它的産出的20%給農業部門,30%給礦業部門,保留餘下的産出. 計算該經濟的交易表,表中的列給出各個部門的産出如何配置設定給其他部門.
考慮例2中的網絡流. 确定
的可能取值範圍. (提示:在例中
. 這對
意味着什麼?同時
習題1.6
假設一個經濟隻有商品和服務兩個部門. 在每一年中,商品部門銷售它的總産出的80%給服務部門,并保留餘下的産出,而服務部門銷售它的總産出的70%給商品部門,并保留餘下的産
出. 找出商品和服務部門的年度産出的平衡價格使得每一部門的收支平衡.
找出例1中經濟的另一組平衡價格.假設同樣的經濟中使用日元而不是美元來衡量各部門的産出值,讨論這個問題會有什麼變化.
考慮一個由燃料動力、制造和服務三個部門構成的經濟體系. 燃料動力部門銷售80%的産出給制造部門和10%的産出給服務部門,保留餘下的産出. 制造部門銷售10%的産出給燃料動力部門和80%的産出給服務部門,保留餘下的産出. 服務部門銷售20%的産出給燃料動力部門和40%的産出給制造部門并保留餘下的産出.
寫出該經濟體系的交易表.
建立方程組表示各部門收支平衡的條件.寫出對應的增廣矩陣以便行化簡求平衡價格.
[m]找出當服務部門産出的價格是100個機關時的一組平衡價格.
假設一個經濟體系有四個部門,分别是礦業(m)、木材(l)、能源(e)和運輸(t)部門. 部門m銷售産出的10%給部門l和60%給部門m并保留餘下的産出. 部門l銷售産出的15%給部門m,50%給部門e和20%給部門t并保留餘下的産出. 部門e銷售産出的20%給部門m,15%給部門l和20%給部門t并保留餘下的産出. 部門t銷售産出的20%給部門m,10%給部門l和50%給部門e并保留餘下的産出.
[m]找出該經濟體系的一組平衡價格.
5.假設一個經濟系統有四個行業構成,分别是農業、制造業、服務業和交通業.農業産出的20%銷售給制造業、30%銷售給服務業、30%銷售給交通業,保留餘下的産出.制造業産出的35%銷售給農業、35%銷售給服務業、20%銷售給交通業,保留餘下的産出.服務業産出的10%銷售給農業、20%銷售給制造業、20%銷售給交通業,保留餘下的産出.交通業産出的20%銷售給農業、30%銷售給制造業、20%銷售給服務業,保留餘下的産出.
a.寫出該經濟系統的交易表;
b.[m]求出當交通業産出的機關價格是10美元時的平衡價格.
c.服務業成功地推出一個“吃農場新鮮”活動,并增加其對農業的銷售份額,增加到40%,而農業産出将降低對制造業的銷售份額,下降到10%.确定這個新經濟系統的行情交易表.
d.[m]當交通業産出的機關價格是10美元時, 求新的平衡價格.“吃農場新鮮”活動對該行業的平衡價格有什麼影響?
習題6~11使用本節讨論的向量方程的方法配平化學方程式.
氧化鋁和碳發生反應生成鋁和二氧化碳
(對每種化合物,構造一個向量列出鋁、氧和碳的原子數目).
alka-seltzer堿性蘇打包含重碳酸鈉( nahco3)和檸檬酸(h3c6h507 ). 當一顆藥片溶解在水中時,會發生化學反應生成檸檬酸鈉、水和二氧化碳(氣體):
碳酸鈣(caco3 )中和酸(h3o ),發生反應産生酸雨,其未配平的化學反應式為
硫化硼與水劇烈反應生成硼酸和硫化氫氣體(臭蛋味).未配平的化學反應式為
[m]如果可能,使用精确的算術或合理的計算格式配平如下的化學反應方程式:
[m]下面的化學反應可以在工業過程中應用,如砷( )的生産. 配平方程式.
求下圖中網絡流量的通解. 假設流量都是非負的,
可能的最小值是什麼?
求下圖中網絡的交通流量的通解.
假設流量必須以标示的方向流動,求分支
的流量的最小值.
求下圖中高速公路網絡的交通流量的通解.(流量以車輛數/分鐘計算.)
求
的道路交通封閉時的交通流量的通解.
當
時,
的最小值是什麼?
英格蘭的交叉路通常被設計成單行的“環行路”,如下圖所示. 假設流量必須以标示的方向流動,求
的最小值.
練習題答案
将比例用小數表示,由于要考慮所有的産出,每列的元素之和等于1. 這種情況有助于填補空缺的元素.